Related: LeetCode 114. Flatten Binary Tree to Linked List
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/
X. Stack
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/252772/Easily-understable-Java-Solution-Runtime-1ms-beat-100-Recursive
http://www.cnblogs.com/grandyang/p/9688522.html
我们其实也可以不用递归,链表的题不像树的题,对于树的题使用递归可以很简洁,而链表递归和迭代可能差的并不多。如果你仔细对比两种方法的代码,你会发现迭代的写法刚好比递归的写法少了调用递归的那一行,给人一种完全没有必要使用递归的感觉,其实两种解法的操作顺序不同的,递归写法是从最底层开始操作,先把最底层加入倒数第二层,再把混合后的层加入倒数第三层,依此类推,直到都融合到第一层为止。而迭代的写法却是反过来的,先把第二层加入第一层,此时第二层底下可能还有很多层,不必理会,之后等遍历到的时候,再一层一层的加入第一层中,不管哪种方法,最终都可以压平
https://www.cnblogs.com/Dylan-Java-NYC/p/9596026.html
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/150321/Easy-Understanding-Java-beat-95.7-with-Explanation
https://hellosmallworld123.wordpress.com/2014/05/29/flatten-a-multilevel-linkedlist/
We approach this problem level by level, first scan all the nodes in the first level, append any list we found in the second level to the end of first level. after we scan to the end of the first level, we will have all the second level appended to the tail. Then we keep going and when we reached the end of the second level, the third level will be appended to the end of the list, and so on. When we finished all the nodes, then we are done.
X. Recursive
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/252772/Easily-understable-Java-Solution-Runtime-1ms-beat-100-Recursive
Time Complexity: O(2n) since in worst case we will visit each node twice. so O(n)
这道题给了我们一个多层的双向链表,让我们压平成为一层的双向链表,题目中给了形象的图例,不难理解题意。根据题目中给的例子,我们可以看出如果某个结点有下一层双向链表,那么下一层双向链表中的结点就要先加入进去,如果下一层链表中某个结点还有下一层,那么还是优先加入下一层的结点,整个加入的机制是DFS的,就是有岔路先走岔路,走到没路了后再返回,这就是深度优先遍历的机制。好,那么既然是DFS,肯定优先考虑递归啦。方法有了,再来看具体怎么递归。由于给定的多层链表本身就是双向的,所以我们只需要把下一层的结点移到第一层即可,那么没有子结点的结点就保持原状,不作处理。只有对于那些有子结点的,我们需要做一些处理,由于子结点链接的双向链表要加到后面,所以当前结点之后要断开,再断开之前,我们用变量next指向下一个链表,然后我们对子结点调用递归函数,我们suppose返回的结点已经压平了,那么就只有一层,那么就相当于要把这一层的结点加到断开的地方,所以我们需要知道这层的最后一个结点的位置,我们用一个变量last,来遍历到压平的这一层的末结点。现在我们就可以开始链接了,首先把子结点链到cur的next,然后把反向指针prev也链上。此时cur的子结点child可以清空,然后压平的这一层的末节点last链上之前保存的next结点,如果next非空,那么链上反向结点prev。这些操作完成后,我们就已经将压平的这一层完整的加入了之前层断开的地方,我们继续在之前层往下遍历即可
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/157606/Java-Recursive-Solution
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/159746/Java-1ms-Recursion-beats-100-with-explaination
Linkedin:
massivealgorithms.blogspot.com/2015/11/linkedin-interview-misc.html
http://www.1point3acres.com/bbs/thread-147555-1-1.html
2. 双向链表,但是每一个点还可以有up,down pointer, 已知一个链表里没有环,要求把这个链表变成标准双向链表,每个点的具体位置排列无所谓。楼主开始反应是递归,写好后面试官说优化一下,,空间要求是constant space,然后尽管面试官一直在提示tail recursion,还是没想出来(据说地里有原题,可惜当时楼主没看到。。。跪了= =!)
Related:
Flattening a Linked List | GeeksforGeeks
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/
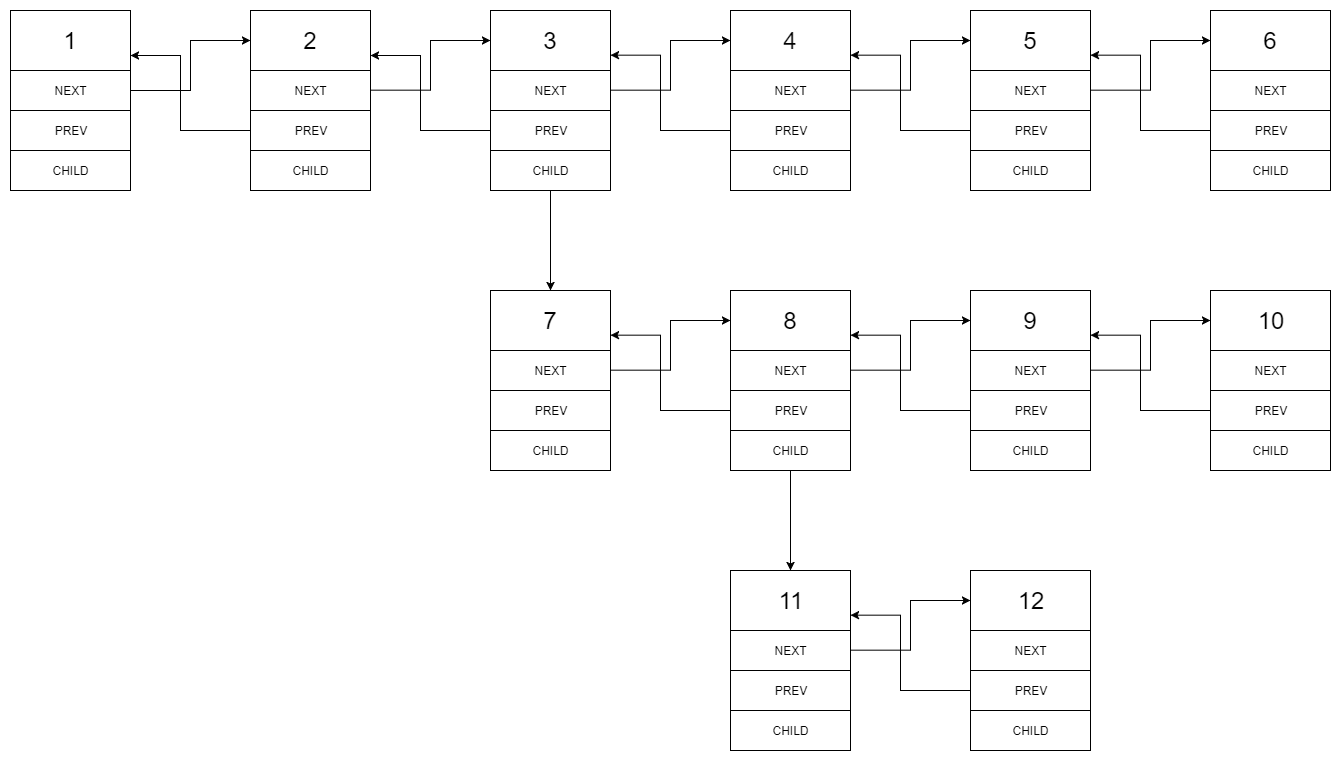
You are given a doubly linked list which in addition to the next and previous pointers, it could have a child pointer, which may or may not point to a separate doubly linked list. These child lists may have one or more children of their own, and so on, to produce a multilevel data structure, as shown in the example below.
Flatten the list so that all the nodes appear in a single-level, doubly linked list. You are given the head of the first level of the list.
Example:
Input: 1---2---3---4---5---6--NULL | 7---8---9---10--NULL | 11--12--NULL Output: 1-2-3-7-8-11-12-9-10-4-5-6-NULL
Explanation for the above example:
Given the following multilevel doubly linked list:
We should return the following flattened doubly linked list:
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/252772/Easily-understable-Java-Solution-Runtime-1ms-beat-100-Recursive
public Node flatten(Node h) {
if (h == null) return h;
Stack<Node> st = new Stack<>();
Node prev = null;
st.push(h);
while (!st.isEmpty()){
Node cur = st.pop();
if (prev != null) {
prev.next = cur;
cur.prev = prev;
prev.child = null;
}
if (cur.next != null) st.push(cur.next);
if (cur.child != null) st.push(cur.child);
prev = cur;
}
return h;
}http://www.cnblogs.com/grandyang/p/9688522.html
我们其实也可以不用递归,链表的题不像树的题,对于树的题使用递归可以很简洁,而链表递归和迭代可能差的并不多。如果你仔细对比两种方法的代码,你会发现迭代的写法刚好比递归的写法少了调用递归的那一行,给人一种完全没有必要使用递归的感觉,其实两种解法的操作顺序不同的,递归写法是从最底层开始操作,先把最底层加入倒数第二层,再把混合后的层加入倒数第三层,依此类推,直到都融合到第一层为止。而迭代的写法却是反过来的,先把第二层加入第一层,此时第二层底下可能还有很多层,不必理会,之后等遍历到的时候,再一层一层的加入第一层中,不管哪种方法,最终都可以压平
https://www.cnblogs.com/Dylan-Java-NYC/p/9596026.html
如果当前点cur 没有child, 直接跳到cur.next 进行下次计算.
如果cur 有child, 目标是把cur.child这个level提到cur这个level上. 至于cur.child 这个level上有没有点有child 先不管.
做法就是cur.child 一直只按next找到tail, 然后这一节插在cur 和 cur.next之间, cur再跳到更新的cur.next上.
Time Complexity: O(n). n是所有点的个数, 每个点只走过constant次数.
20 public Node flatten(Node head) { 21 if(head == null){ 22 return head; 23 } 24 25 Node cur = head; 26 while(cur != null){ 27 if(cur.child == null){ 28 cur = cur.next; 29 continue; 30 } 31 32 Node child = cur.child; 33 Node childTail = child; 34 while(childTail.next != null){ 35 childTail = childTail.next; 36 } 37 38 cur.child = null; 39 child.prev = cur; 40 childTail.next = cur.next; 41 if(cur.next != null){ 42 cur.next.prev = childTail; 43 } 44 cur.next = child; 45 cur = cur.next; 46 } 47 48 return head; 49 }
- Start form the
head, move one step each time to the next node - When meet with a node with child, say node
p, follow itschild chainto the end and connect the tail node withp.next, by doing this we merged thechild chainback to themain thread - Return to
pand proceed until find next node with child. - Repeat until reach
null
It seems still to be an O(n) solution. Since we need to visit each node at most twice, one for find the tail of the current branch, and the other for flatten the current node. Correct me if I am wrong.
If so, this is a really nice solution with O(n) time and O(1) space!
If so, this is a really nice solution with O(n) time and O(1) space!
This is more like a top down flattening, when encounter a node with child node, we directly flatten the current node, then move to the next node.
the recursive method is more like bottom up flattening, means when we encounter a node with child node, we flatten the child node first, then flatten the current node.
the recursive method is more like bottom up flattening, means when we encounter a node with child node, we flatten the child node first, then flatten the current node.
public Node flatten(Node head) {
if( head == null) return head;
// Pointer
Node p = head;
while( p!= null) {
/* CASE 1: if no child, proceed */
if( p.child == null ) {
p = p.next;
continue;
}
/* CASE 2: got child, find the tail of the child and link it to p.next */
Node temp = p.child;
// Find the tail of the child
while( temp.next != null )
temp = temp.next;
// Connect tail with p.next, if it is not null
temp.next = p.next;
if( p.next != null ) p.next.prev = temp;
// Connect p with p.child, and remove p.child
p.next = p.child;
p.child.prev = p;
p.child = null;
}
return head;
}https://hellosmallworld123.wordpress.com/2014/05/29/flatten-a-multilevel-linkedlist/
We approach this problem level by level, first scan all the nodes in the first level, append any list we found in the second level to the end of first level. after we scan to the end of the first level, we will have all the second level appended to the tail. Then we keep going and when we reached the end of the second level, the third level will be appended to the end of the list, and so on. When we finished all the nodes, then we are done.
class ListNode { int label; ListNode child; ListNode next; public ListNode(int l) { label = l; }} public ListNode flattenList(ListNode head) { if (head == null) return null; ListNode curr = head; ListNode tail = head; // find the tail of the list while(tail.next != null) { tail = tail.next; } while(curr != null) { if (curr.child != null) { tail.next = curr.child; // move tail to the end tail while(tail.next != null) tail = tail.next; curr.child = null; } curr = curr.next; } return head; }1) Take "cur" pointer, which will point to head of the fist level of the list
2) Take "tail" pointer, which will point to end of the first level of the list
3) Repeat the below procedure while "curr" is not NULL.
I) if current node has a child then
a) append this new child list to the "tail"
tail->next = cur->child
b) find the last node of new child list and update "tail"
tmp = cur->child;
while (tmp->next != NULL)
tmp = tmp->next;
tail = tmp;
II) move to the next node. i.e. cur = cur->next
void flattenList(struct node *head){ /*Base case*/ if (head == NULL) return; struct node *tmp; /* Find tail node of first level linked list */ struct node *tail = head; while (tail->next != NULL) tail = tail->next; // One by one traverse through all nodes of first level // linked list till we reach the tail node struct node *cur = head; while (cur != tail) { // If current node has a child if (cur->child) { // then append the child at the end of current list tail->next = cur->child; // and update the tail to new last node tmp = cur->child; while (tmp->next) tmp = tmp->next; tail = tmp; } // Change current node cur = cur->next; }}https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/252772/Easily-understable-Java-Solution-Runtime-1ms-beat-100-Recursive
Traverse through the linked list and whenever you find a node with a child, call flatten function recursively on that child node.
Also, don't forget to maintain a class variable which will keep last visited node which will act as a tail pointer.
Also, don't forget to maintain a class variable which will keep last visited node which will act as a tail pointer.
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/157606/Java-Recursive-Solution
https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/159746/Java-1ms-Recursion-beats-100-with-explaination
Go through the linked list;
If
If
- Node cur.child == null, skip, don't go into recursion.
- Node cur.child != null, recurse and get child's tail node. Node tmp = cur.next, (1)connect cur <-> child, (2)connect child's tail <->tmp.
The helper function returns the tail node of current level.
public Node flatten(Node head) {
helper(head);
return head;
}
private Node helper(Node head) {
Node cur = head, pre = head;
while(cur != null) {
if(cur.child == null) {
pre = cur;
cur = cur.next;
} else {
Node tmp = cur.next;
Node child = helper(cur.child);
cur.next = cur.child;
cur.child.prev = cur;
cur.child = null;
child.next = tmp;
if(tmp != null) tmp.prev = child;
pre = child;
cur = tmp;
}
}
return pre;
}
The idea is simple. We always keep a
pre global variable to keep track of the last node we visited and connect current node head with this pre node. So for each recursive call, we do- Connect last visited node with current node by letting
pre.nextpoint to current nodeheadand current node'sprevpoint topre - Mark current node as pre.
pre = head - If there is
head.child, we recursively visit and flatten its child node - Recursively visit and flatten its next node
/*Global variable pre to track the last node we visited */
Node pre = null;
public Node flatten(Node head) {
if (head == null) {
return null;
}
/*Connect last visted node with current node */
if (pre != null) {
pre.next = head;
head.prev = pre;
}
pre = head;
/*Store head.next in a next pointer in case recursive call to flatten head.child overrides head.next*/
Node next = head.next;
flatten(head.child);
head.child = null;
flatten(next);
return head;
}Linkedin:
massivealgorithms.blogspot.com/2015/11/linkedin-interview-misc.html
http://www.1point3acres.com/bbs/thread-147555-1-1.html
2. 双向链表,但是每一个点还可以有up,down pointer, 已知一个链表里没有环,要求把这个链表变成标准双向链表,每个点的具体位置排列无所谓。楼主开始反应是递归,写好后面试官说优化一下,,空间要求是constant space,然后尽管面试官一直在提示tail recursion,还是没想出来(据说地里有原题,可惜当时楼主没看到。。。跪了= =!)
Related:
Flattening a Linked List | GeeksforGeeks
Given a linked list where every node represents a linked list and contains two pointers of its type:
(i) Pointer to next node in the main list (we call it ‘right’ pointer in below code)
(ii) Pointer to a linked list where this node is head (we call it ‘down’ pointer in below code).
All linked lists are sorted. See the following example
(i) Pointer to next node in the main list (we call it ‘right’ pointer in below code)
(ii) Pointer to a linked list where this node is head (we call it ‘down’ pointer in below code).
All linked lists are sorted. See the following example
5 -> 10 -> 19 -> 28
| | | |
V V V V
7 20 22 35
| | |
V V V
8 50 40
| |
V V
30 45
Write a function flatten() to flatten the lists into a single linked list. The flattened linked list should also be sorted. For example, for the above input list, output list should be 5->7->8->10->19->20->22->28->30->35->40->45->50.
The idea is to use Merge() process of merge sort for linked lists. We use merge() to merge lists one by one. We recursively merge() the current list with already flattened list.
The down pointer is used to link nodes of the flattened list.
Read full article from Flatten a multilevel linked list | GeeksforGeeksThe down pointer is used to link nodes of the flattened list.