Count Inversions in an array | GeeksforGeeks
https://github.com/epibook/epibook.github.io/blob/master/static/solutions/java/src/main/java/com/epi/CountInversions.java
private static int countSubarrayInversions(List<Integer> A, int start,
int end) {
if (end - start <= 1) {
return 0;
}
int mid = start + ((end - start) / 2);
return countSubarrayInversions(A, start, mid)
+ countSubarrayInversions(A, mid, end)
+ mergeSortAndCountInversionsAcrossSubarrays(A, start, mid, end);
}
// Merge two sorted sublists AsubList(start, mid) and A.subList(mid, end)
// into A.subList(start, end) and return the number of inversions across
// A.subList(start, mid) and A.subList(mid, end).
private static int mergeSortAndCountInversionsAcrossSubarrays(List<Integer> A,
int start,
int mid,
int end) {
List<Integer> sortedA = new ArrayList<>();
int leftStart = start, rightStart = mid, inversionCount = 0;
while (leftStart < mid && rightStart < end) {
if (Integer.compare(A.get(leftStart), A.get(rightStart)) <= 0) {
sortedA.add(A.get(leftStart++));
} else {
// A.subList(leftStart, mid) are the inversions of A[rightStart].
inversionCount += mid - leftStart;
sortedA.add(A.get(rightStart++));
}
}
sortedA.addAll(A.subList(leftStart, mid));
sortedA.addAll(A.subList(rightStart, end));
// Updates A with sortedA.
for (Integer t : sortedA) {
A.set(start++, t);
}
return inversionCount;
}
From http://www.programminggeek.in/2013/07/c-and-java-program-for-counting-number-of-inversion-in-
Number of an inversion in array is the number of pair(a[i],a[j]) of elements such that i < j and a[i] > a[j]. For an example if we have a list of element 2 3 6 9 1 then number of inversion is 4 and the pairs are (2,1), (3,1), (6,1) and (9,1)
This algorithm is based on Divide and Conquer paradigm. It is implemented using merge sort. In this approach the time complexity will be O(n log(n)) . Actually in divide step we divide the problem in two parts. And then two parts are solved recursively. The key concept is two count the number of inversion in merge procedure. In merge procedure we pass two sub-list. The element is sorted and inversion is found as follows :
http://www.geeksforgeeks.org/counting-inversions/
http://www.programminggeek.in/2013/07/c-and-java-program-for-counting-number-of-inversion-in-
https://cgi.csc.liv.ac.uk/~martin/teaching/comp202/Java/Inversions-code.html
[剑指Offer] 数据组的逆序对
O(N^2)
http://rafal.io/posts/codility-inversion-count.html
Merge sort - iterative version:
http://codility-lessons.blogspot.com/2015/04/lesson-99-arrayinversioncount-array.html
X. Using binary search tree
https://www.geeksforgeeks.org/count-inversions-in-an-array-set-2-using-self-balancing-bst/
// A utility function to right rotate subtree rooted with y
http://www.geeksforgeeks.org/count-inversions-array-set-3-using-bit/
http://algs4.cs.princeton.edu/22mergesort/Inversions.java.html
Read full article from Count Inversions in an array | GeeksforGeeks
Inversion Count for an array indicates – how far (or close) the array is from being sorted. If array is already sorted then inversion count is 0. If array is sorted in reverse order that inversion count is the maximum.
Formally speaking, two elements a[i] and a[j] form an inversion if a[i] > a[j] and i < j
Formally speaking, two elements a[i] and a[j] form an inversion if a[i] > a[j] and i < j
Example:
The sequence 2, 4, 1, 3, 5 has three inversions (2, 1), (4, 1), (4, 3).
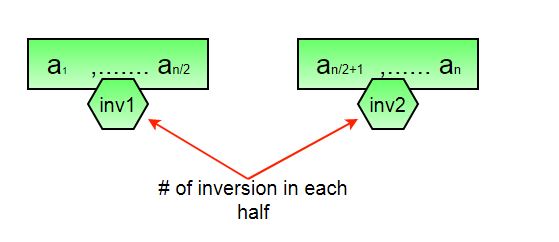
How to get number of inversions in merge()?
In merge process, let i is used for indexing left sub-array and j for right sub-array. At any step in merge(), if a[i] is greater than a[j], then there are (mid – i) inversions. because left and right subarrays are sorted, so all the remaining elements in left-subarray (a[i+1], a[i+2] … a[mid]) will be greater than a[j]
The sequence 2, 4, 1, 3, 5 has three inversions (2, 1), (4, 1), (4, 3).
METHOD 2(Enhance Merge Sort)
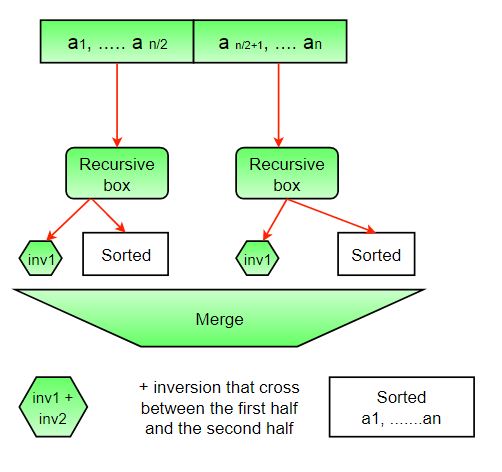
Suppose we know the number of inversions in the left half and right half of the array (let be inv1 and inv2), what kinds of inversions are not accounted for in Inv1 + Inv2? The answer is – the inversions we have to count during the merge step. Therefore, to get number of inversions, we need to add number of inversions in left subarray, right subarray and merge().
Suppose we know the number of inversions in the left half and right half of the array (let be inv1 and inv2), what kinds of inversions are not accounted for in Inv1 + Inv2? The answer is – the inversions we have to count during the merge step. Therefore, to get number of inversions, we need to add number of inversions in left subarray, right subarray and merge().

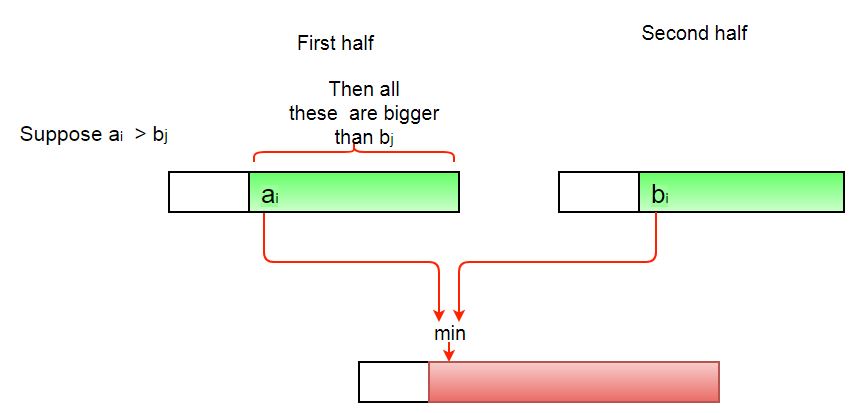
How to get number of inversions in merge()?
In merge process, let i is used for indexing left sub-array and j for right sub-array. At any step in merge(), if a[i] is greater than a[j], then there are (mid – i) inversions. because left and right subarrays are sorted, so all the remaining elements in left-subarray (a[i+1], a[i+2] … a[mid]) will be greater than a[j]

The complete picture:

static int mergeSort(int arr[], int array_size) { int temp[] = new int[array_size]; return _mergeSort(arr, temp, 0, array_size - 1); } /* An auxiliary recursive method that sorts the input array and returns the number of inversions in the array. */ static int _mergeSort(int arr[], int temp[], int left, int right) { int mid, inv_count = 0; if (right > left) { /* Divide the array into two parts and call _mergeSortAndCountInv() for each of the parts */ mid = (right + left)/2; /* Inversion count will be sum of inversions in left-part, right-part and number of inversions in merging */ inv_count = _mergeSort(arr, temp, left, mid); inv_count += _mergeSort(arr, temp, mid+1, right); /*Merge the two parts*/ inv_count += merge(arr, temp, left, mid+1, right); } return inv_count; } /* This method merges two sorted arrays and returns inversion count in the arrays.*/ static int merge(int arr[], int temp[], int left, int mid, int right) { int i, j, k; int inv_count = 0; i = left; /* i is index for left subarray*/ j = mid; /* j is index for right subarray*/ k = left; /* k is index for resultant merged subarray*/ while ((i <= mid - 1) && (j <= right)) { if (arr[i] <= arr[j]) { temp[k++] = arr[i++]; } else { temp[k++] = arr[j++]; /*this is tricky -- see above explanation/diagram for merge()*/ inv_count = inv_count + (mid - i); } } /* Copy the remaining elements of left subarray (if there are any) to temp*/ while (i <= mid - 1) temp[k++] = arr[i++]; /* Copy the remaining elements of right subarray (if there are any) to temp*/ while (j <= right) temp[k++] = arr[j++]; /*Copy back the merged elements to original array*/ for (i=left; i <= right; i++) arr[i] = temp[i]; return inv_count; }EPI Solution: Count inversions
Count_inversions.cpp CountInversions.javahttps://github.com/epibook/epibook.github.io/blob/master/static/solutions/java/src/main/java/com/epi/CountInversions.java
private static int countSubarrayInversions(List<Integer> A, int start,
int end) {
if (end - start <= 1) {
return 0;
}
int mid = start + ((end - start) / 2);
return countSubarrayInversions(A, start, mid)
+ countSubarrayInversions(A, mid, end)
+ mergeSortAndCountInversionsAcrossSubarrays(A, start, mid, end);
}
// Merge two sorted sublists AsubList(start, mid) and A.subList(mid, end)
// into A.subList(start, end) and return the number of inversions across
// A.subList(start, mid) and A.subList(mid, end).
private static int mergeSortAndCountInversionsAcrossSubarrays(List<Integer> A,
int start,
int mid,
int end) {
List<Integer> sortedA = new ArrayList<>();
int leftStart = start, rightStart = mid, inversionCount = 0;
while (leftStart < mid && rightStart < end) {
if (Integer.compare(A.get(leftStart), A.get(rightStart)) <= 0) {
sortedA.add(A.get(leftStart++));
} else {
// A.subList(leftStart, mid) are the inversions of A[rightStart].
inversionCount += mid - leftStart;
sortedA.add(A.get(rightStart++));
}
}
sortedA.addAll(A.subList(leftStart, mid));
sortedA.addAll(A.subList(rightStart, end));
// Updates A with sortedA.
for (Integer t : sortedA) {
A.set(start++, t);
}
return inversionCount;
}
From http://www.programminggeek.in/2013/07/c-and-java-program-for-counting-number-of-inversion-in-
Number of an inversion in array is the number of pair(a[i],a[j]) of elements such that i < j and a[i] > a[j]. For an example if we have a list of element 2 3 6 9 1 then number of inversion is 4 and the pairs are (2,1), (3,1), (6,1) and (9,1)
This algorithm is based on Divide and Conquer paradigm. It is implemented using merge sort. In this approach the time complexity will be O(n log(n)) . Actually in divide step we divide the problem in two parts. And then two parts are solved recursively. The key concept is two count the number of inversion in merge procedure. In merge procedure we pass two sub-list. The element is sorted and inversion is found as follows :
http://www.geeksforgeeks.org/counting-inversions/
http://www.programminggeek.in/2013/07/c-and-java-program-for-counting-number-of-inversion-in-
https://cgi.csc.liv.ac.uk/~martin/teaching/comp202/Java/Inversions-code.html
[剑指Offer] 数据组的逆序对
int _mergeSort(int arr[], int temp[], int left, int right);int merge(int arr[], int temp[], int left, int mid, int right); /* This function sorts the input array and returns the number of inversions in the array */int mergeSort(int arr[], int array_size){ int *temp = (int *)malloc(sizeof(int)*array_size); return _mergeSort(arr, temp, 0, array_size - 1);} /* An auxiliary recursive function that sorts the input array and returns the number of inversions in the array. */int _mergeSort(int arr[], int temp[], int left, int right){ int mid, inv_count = 0; if (right > left) { /* Divide the array into two parts and call _mergeSortAndCountInv() for each of the parts */ mid = (right + left)/2; /* Inversion count will be sum of inversions in left-part, right-part and number of inversions in merging */ inv_count = _mergeSort(arr, temp, left, mid); inv_count += _mergeSort(arr, temp, mid+1, right); /*Merge the two parts*/ inv_count += merge(arr, temp, left, mid+1, right); } return inv_count;} /* This funt merges two sorted arrays and returns inversion count in the arrays.*/int merge(int arr[], int temp[], int left, int mid, int right){ int i, j, k; int inv_count = 0; i = left; /* i is index for left subarray*/ j = mid; /* i is index for right subarray*/ k = left; /* i is index for resultant merged subarray*/ while ((i <= mid - 1) && (j <= right)) { if (arr[i] <= arr[j]) { temp[k++] = arr[i++]; } else { temp[k++] = arr[j++]; /*this is tricky -- see above explanation/diagram for merge()*/ inv_count = inv_count + (mid - i); } } /* Copy the remaining elements of left subarray (if there are any) to temp*/ while (i <= mid - 1) temp[k++] = arr[i++]; /* Copy the remaining elements of right subarray (if there are any) to temp*/ while (j <= right) temp[k++] = arr[j++]; /*Copy back the merged elements to original array*/ for (i=left; i <= right; i++) arr[i] = temp[i]; return inv_count;} int getInvCount(int arr[], int n){ int inv_count = 0; int i, j; for(i = 0; i < n - 1; i++) for(j = i+1; j < n; j++) if(arr[i] > arr[j]) inv_count++; return inv_count;}http://rafal.io/posts/codility-inversion-count.html
Merge sort - iterative version:
http://codility-lessons.blogspot.com/2015/04/lesson-99-arrayinversioncount-array.html
int solution(int A[], int N)
{
int cnt = 0;
int memsize = sizeof(int) * N;
int*work = (int*)alloca(memsize);
for (int blksize = 1; blksize < N; blksize *= 2){
int lpos = 0;
int rpos = blksize;
//merge each blocks
while(lpos <= N){
int writebackpos = lpos;
int lend = lpos + blksize;
lend = lend >= N ? N : lend;
int rend = rpos + blksize;
rend = rend >= N ? N : rend;
//merge
int wpos = 0;
while (lpos < lend && rpos < rend){
if (A[lpos] <= A[rpos]){
work[wpos++] = A[lpos++];
}
else {
work[wpos++] = A[rpos++];
cnt += lend - lpos;
if (cnt >= 1000000000){
return - 1;
}
}
}
while (lpos < lend){
work[wpos++] = A[lpos++];
}
while (rpos < rend){
work[wpos++] = A[rpos++];
}
//write back
memcpy(A + writebackpos, work, sizeof(int) * wpos);
//proceed to the next block
lpos = rpos;
rpos = lpos + blksize;
}
}
return cnt;
}
X. Using binary search tree
https://www.geeksforgeeks.org/count-inversions-in-an-array-set-2-using-self-balancing-bst/
1) Create an empty AVL Tree. The tree is augmented here
such that every node also maintains size of subtree
rooted with this node.
2) Initialize inversion count or result as 0.
3) Iterate from 0 to n-1 and do following for every
element in arr[i]
a) Insert arr[i] into the AVL Tree. The insertion
operation also updates result. The idea is to
keep counting greater nodes when tree is traversed
from root to a leaf for insertion.
4) Return result.
1) When we insert arr[i], elements from arr[0] to arr[i-1] are already inserted into AVL Tree. All we need to do is count these nodes.
2) For insertion into AVL Tree, we traverse tree from root to a leaf by comparing every node with arr[i[]. When arr[i[ is smaller than current node, we increase inversion count by 1 plus the number of nodes in right subtree of current node. Which is basically count of greater elements on left of arr[i], i.e., inversions.
2) For insertion into AVL Tree, we traverse tree from root to a leaf by comparing every node with arr[i[]. When arr[i[ is smaller than current node, we increase inversion count by 1 plus the number of nodes in right subtree of current node. Which is basically count of greater elements on left of arr[i], i.e., inversions.
struct Node *rightRotate(struct Node *y){ struct Node *x = y->left; struct Node *T2 = x->right; // Perform rotation x->right = y; y->left = T2; // Update heights y->height = max(height(y->left), height(y->right))+1; x->height = max(height(x->left), height(x->right))+1; // Update sizes y->size = size(y->left) + size(y->right) + 1; x->size = size(x->left) + size(x->right) + 1; // Return new root return x;}// A utility function to left rotate subtree rooted with xstruct Node *leftRotate(struct Node *x){ struct Node *y = x->right; struct Node *T2 = y->left; // Perform rotation y->left = x; x->right = T2; // Update heights x->height = max(height(x->left), height(x->right))+1; y->height = max(height(y->left), height(y->right))+1; // Update sizes x->size = size(x->left) + size(x->right) + 1; y->size = size(y->left) + size(y->right) + 1; // Return new root return y;}// Get Balance factor of Node Nint getBalance(struct Node *N){ if (N == NULL) return 0; return height(N->left) - height(N->right);}// Inserts a new key to the tree rotted with Node. Also, updates// *result (inversion count)struct Node* insert(struct Node* node, int key, int *result){ /* 1. Perform the normal BST rotation */ if (node == NULL) return(newNode(key)); if (key < node->key) { node->left = insert(node->left, key, result); // UPDATE COUNT OF GREATE ELEMENTS FOR KEY *result = *result + size(node->right) + 1; } else node->right = insert(node->right, key, result); /* 2. Update height and size of this ancestor node */ node->height = max(height(node->left), height(node->right)) + 1; node->size = size(node->left) + size(node->right) + 1; /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ int balance = getBalance(node); // If this node becomes unbalanced, then there are // 4 cases // Left Left Case if (balance > 1 && key < node->left->key) return rightRotate(node); // Right Right Case if (balance < -1 && key > node->right->key) return leftRotate(node); // Left Right Case if (balance > 1 && key > node->left->key) { node->left = leftRotate(node->left); return rightRotate(node); } // Right Left Case if (balance < -1 && key < node->right->key) { node->right = rightRotate(node->right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node;}// The following function returns inversion count in arr[]int getInvCount(int arr[], int n){ struct Node *root = NULL; // Create empty AVL Tree int result = 0; // Initialize result // Starting from first element, insert all elements one by // one in an AVL tree. for (int i=0; i<n; i++) // Note that address of result is passed as insert // operation updates result by adding count of elements // greater than arr[i] on left of arr[i] root = insert(root, arr[i], &result); return result;}
BIT basically supports two operations for an array arr[] of size n:
- Sum of elements till arr[i] in O(Log n) time.
- Update an array element in O(Log n) time.
BIT is implemented using an array and works in form of trees. Note that there are two ways of looking at BIT as a tree.
- The sum operation where parent of index x is "x - (x & -x)".
- The update operation where parent of index x is "x + (x & -x)".
We recommend you refer Binary Indexed Tree (BIT) before further reading this post.
Basic Approach using BIT of size Θ(maxElement):
The idea is to iterate the array from n-1 to 0. When we are at i'th index, we check how many numbers less than arr[i] are present in BIT and add it to the result. To get the count of smaller elements, getSum() of BIT is used. In his basic idea, BIT is represented as an array of size equal to maximum element plus one. So that elements can be used as an index.
After that we add current element to to the BIT[] by doing an update operation that updates count of current element from 0 to 1, and therefore updates ancestors of current element in BIT (See update() in BIT for details).
The idea is to iterate the array from n-1 to 0. When we are at i'th index, we check how many numbers less than arr[i] are present in BIT and add it to the result. To get the count of smaller elements, getSum() of BIT is used. In his basic idea, BIT is represented as an array of size equal to maximum element plus one. So that elements can be used as an index.
After that we add current element to to the BIT[] by doing an update operation that updates count of current element from 0 to 1, and therefore updates ancestors of current element in BIT (See update() in BIT for details).
// Returns sum of arr[0..index]. This function assumes
// that the array is preprocessed and partial sums of// array elements are stored in BITree[].int getSum(int BITree[], int index){ int sum = 0; // Initialize result // Traverse ancestors of BITree[index] while (index > 0) { // Add current element of BITree to sum sum += BITree[index]; // Move index to parent node in getSum View index -= index & (-index); } return sum;}// Updates a node in Binary Index Tree (BITree) at given index// in BITree. The given value 'val' is added to BITree[i] and// all of its ancestors in tree.void updateBIT(int BITree[], int n, int index, int val){ // Traverse all ancestors and add 'val' while (index <= n) { // Add 'val' to current node of BI Tree BITree[index] += val; // Update index to that of parent in update View index += index & (-index); }}// Returns inversion count arr[0..n-1]int getInvCount(int arr[], int n){ int invcount = 0; // Initialize result // Find maximum element in arr[] int maxElement = 0; for (int i=0; i<n; i++) if (maxElement < arr[i]) maxElement = arr[i]; // Create a BIT with size equal to maxElement+1 (Extra // one is used so that elements can be directly be // used as index) int BIT[maxElement+1]; for (int i=1; i<=maxElement; i++) BIT[i] = 0; // Traverse all elements from right. for (int i=n-1; i>=0; i--) { // Get count of elements smaller than arr[i] invcount += getSum(BIT, arr[i]-1); // Add current element to BIT updateBIT(BIT, maxElement, arr[i], 1); } return invcount;} |
Time Complexity :- The update function and getSum function runs for O(log(maximumelement)) and we are iterating over n elements. So overall time complexity is : O(nlog(maximumelement)).
Auxiliary space : O(maxElement)
Auxiliary space : O(maxElement)
Better Approach using BIT of size Θ(n):
The problem with the previous approach is that it doesn't work for negative numbers as index cannot be negative. Also by updating the value till maximum element we waste time and space as it is quite possible that we may never use intermediate value. For example, lots of space an time is wasted for an array like {1, 100000}.
The problem with the previous approach is that it doesn't work for negative numbers as index cannot be negative. Also by updating the value till maximum element we waste time and space as it is quite possible that we may never use intermediate value. For example, lots of space an time is wasted for an array like {1, 100000}.
The idea is to convert given array to an array with values from 1 to n and relative order of smaller and greater elements remains
Example :-
arr[] = {7, -90, 100, 1}
It gets converted to,
arr[] = {3, 1, 4 ,2 }
as -90 < 1 < 7 < 100.
We only have to make BIT[] of number of elements instead of maximum element.
Changing element will not have any change in the answer as the greater elements remain greater and at same position
Changing element will not have any change in the answer as the greater elements remain greater and at same position
// Returns sum of arr[0..index]. This function assumes
// that the array is preprocessed and partial sums of// array elements are stored in BITree[].int getSum(int BITree[], int index){ int sum = 0; // Initialize result // Traverse ancestors of BITree[index] while (index > 0) { // Add current element of BITree to sum sum += BITree[index]; // Move index to parent node in getSum View index -= index & (-index); } return sum;}// Updates a node in Binary Index Tree (BITree) at given index// in BITree. The given value 'val' is added to BITree[i] and// all of its ancestors in tree.void updateBIT(int BITree[], int n, int index, int val){ // Traverse all ancestors and add 'val' while (index <= n) { // Add 'val' to current node of BI Tree BITree[index] += val; // Update index to that of parent in update View index += index & (-index); }}// Converts an array to an array with values from 1 to n// and relative order of smaller and greater elements remains// same. For example, {7, -90, 100, 1} is converted to// {3, 1, 4 ,2 }void convert(int arr[], int n){ // Create a copy of arrp[] in temp and sort the temp array // in increasing order int temp[n]; for (int i=0; i<n; i++) temp[i] = arr[i]; sort(temp, temp+n); // Traverse all array elements for (int i=0; i<n; i++) { // lower_bound() Returns pointer to the first element // greater than or equal to arr[i] arr[i] = lower_bound(temp, temp+n, arr[i]) - temp + 1; }}// Returns inversion count arr[0..n-1]int getInvCount(int arr[], int n){ int invcount = 0; // Initialize result // Convert arr[] to an array with values from 1 to n and // relative order of smaller and greater elements remains // same. For example, {7, -90, 100, 1} is converted to // {3, 1, 4 ,2 } convert(arr, n); // Create a BIT with size equal to maxElement+1 (Extra // one is used so that elements can be directly be // used as index) int BIT[n+1]; for (int i=1; i<=n; i++) BIT[i] = 0; // Traverse all elements from right. for (int i=n-1; i>=0; i--) { // Get count of elements smaller than arr[i] invcount += getSum(BIT, arr[i]-1); // Add current element to BIT updateBIT(BIT, n, arr[i], 1); } return invcount;} |
http://algs4.cs.princeton.edu/22mergesort/Inversions.java.html
Read full article from Count Inversions in an array | GeeksforGeeks