https://leetcode.com/problems/minimum-score-triangulation-of-polygon/
Given
N, consider a convex N-sided polygon with vertices labelled A[0], A[i], ..., A[N-1] in clockwise order.
Suppose you triangulate the polygon into
N-2 triangles. For each triangle, the value of that triangle is the product of the labels of the vertices, and the total score of the triangulation is the sum of these values over all N-2 triangles in the triangulation.
Return the smallest possible total score that you can achieve with some triangulation of the polygon.
Example 1:
Input: [1,2,3] Output: 6 Explanation: The polygon is already triangulated, and the score of the only triangle is 6.
Example 2:

Input: [3,7,4,5] Output: 144 Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144. The minimum score is 144.
Example 3:
Input: [1,3,1,4,1,5] Output: 13 Explanation: The minimum score triangulation has score 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.
Note:
3 <= A.length <= 501 <= A[i] <= 100
https://h1ros.github.io/posts/coding/1039-minimum-score-triangulation-of-polygon/
The connected two points in polygon shares one common edge,
these two points must be one and only one triangles.
these two points must be one and only one triangles.
Explanation
dp[i][j] means the minimum score to triangulate A[i] ~ A[j],while there is edge connect
A[i] and A[j].
We enumerate all points
A[k] with i < k < j to form a triangle.
The score of this triangulation is
dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[j] * A[k]
Java, bottom-up:
public int minScoreTriangulation(int[] A) {
int n = A.length;
int[][] dp = new int[n][n];
for (int d = 2; d < n; ++d) {
for (int i = 0; i + d < n; ++i) {
int j = i + d;
dp[i][j] = Integer.MAX_VALUE;
for (int k = i + 1; k < j; ++k)
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[j] * A[k]);
}
}
return dp[0][n - 1];
}
Java, bottom-up, another loop version
public int minScoreTriangulation(int[] A) {
int n = A.length;
int[][] dp = new int[n][n];
for (int j = 2; j < n; ++j) {
for (int i = j - 2; i >= 0; --i) {
dp[i][j] = Integer.MAX_VALUE;
for (int k = i + 1; k < j; ++k)
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[j] * A[k]);
}
}
return dp[0][n - 1];
}
If we pick a side of our polygon, it can form
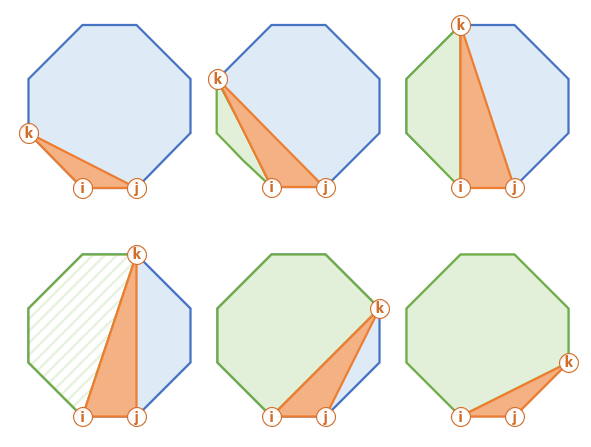
This is how this procedure looks for a sub-polygon (filled with diagonal pattern above).
n - 2 triangles. Each such triangle forms 2 sub-polygons. We can analyze n - 2 triangles, and get the minimum score for sub-polygons using the recursion.
This is how this procedure looks for a sub-polygon (filled with diagonal pattern above).
Top-Down Solution
• Fix one side of the polygon i, j and move k within (i, j).
• Calculate score of the i, k, j "orange" triangle.
• Add the score of the "green" polygon i, k using recursion.
• Add the score of the "blue" polygon k, j using recursion.
• Use memoisation to remember minimum scores for each sub-polygons.
• Calculate score of the i, k, j "orange" triangle.
• Add the score of the "green" polygon i, k using recursion.
• Add the score of the "blue" polygon k, j using recursion.
• Use memoisation to remember minimum scores for each sub-polygons.
int dp[50][50] = {};
int minScoreTriangulation(vector<int>& A, int i = 0, int j = 0, int res = 0) {
if (j == 0) j = A.size() - 1;
if (dp[i][j] != 0) return dp[i][j];
for (auto k = i + 1; k < j; ++k) {
res = min(res == 0 ? INT_MAX : res,
minScoreTriangulation(A, i, k) + A[i] * A[k] * A[j] + minScoreTriangulation(A, k, j));
}
return dp[i][j] = res;
}
Bottom-Up Solution
At this point, it should not be hard to come up with a bottom-up solution. The only trick here is to move
i backward. This ensures "green" and "blue" sub-polygons are processed before calculating min value for the entire polygon. It happens this way naturally with the recursive solution.int minScoreTriangulation(vector<int>& A) {
int dp[50][50] = {};
for (int i = A.size() - 1; i >= 0; --i)
for (int j = i + 1; j < A.size(); ++j)
for (auto k = i + 1; k < j; ++k)
dp[i][j] = min(dp[i][j] == 0 ? INT_MAX : dp[i][j], dp[i][k] + A[i] * A[k] * A[j] + dp[k][j]);
return dp[0][A.size() - 1];
}
Complexity Analysis
Runtime: O(n ^ 3). This can be easily seen from the bottom-up solution.
Memory: O(n ^ 2). We use a square matrix to store DP results
Memory: O(n ^ 2). We use a square matrix to store DP results
https://www.acwing.com/solution/LeetCode/content/2474/
给定
N,想象一个凸 N 边多边形,其顶点按顺时针顺序依次标记为 A[0], A[i], ..., A[N-1]。
假设您将多边形剖分为
N-2 个三角形。对于每个三角形,该三角形的值是顶点标记的乘积,三角剖分的分数是进行三角剖分后所有 N-2 个三角形的值之和。
返回多边形进行三角剖分后可以得到的最低分。
样例
输入:[1,2,3]
输出:6
解释:多边形已经三角化,唯一三角形的分数为 6。

输入:[3,7,4,5]
输出:144
解释:有两种三角剖分,可能得分分别为:3*7*5 + 4*5*7 = 245,或 3*4*5 + 3*4*7 = 144。最低分数为 144。
输入:[1,3,1,4,1,5]
输出:13
解释:最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。
注意
3 <= A.length <= 501 <= A[i] <= 100
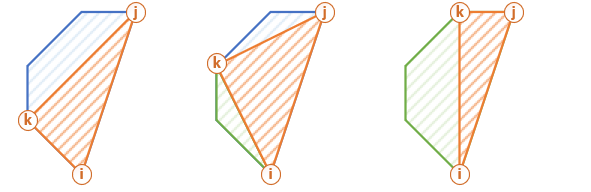
- 我们首先分析一下划分的过程。假设一开始所有点之间都没有连线(包括相邻的点),我们任选两个点 作为初始的点对,将 s 和 t连线。
- 此时整个凸多边形被划分为两段连续的部分。对于其中一部分,任选一个没有被连接的点 u,与 s 和 t 分别连线,组成一个三角形,则 和 可以将那一部分进一步划分。
- 通过这样的分析,我们可以看出,每次划分的都是连续的一段区间,我们从连续的一段区间中找到一个点,将这段连续的区间划分为更小的区间,这显然满足区间动态规划的基本模型。
- 因为图形是环形的,首先考虑将点拷贝一份接到最后,即
A[0], A[1], ..., A[N - 1], A[0], A[1], ..., A[N - 1],共计 个点。设状态 表示划分区间 的最小代价(其中点对 已经连线)。 - 初始值 。转移时,枚举除了 i 和 j 之外的点 k,让 组成一个三角形,即 。
- 找最终答案时,需要枚举初始的连线 ,,找 。
时间复杂度
- 状态数为 ,每次转移需要枚举 个状态,故时间复杂度为 。
空间复杂度
- 需要记录状态,故空间复杂度为 。
- 输入一个整数数组, 数组的index表示一个平面上点的index, 这样就组成一个多边形;
- 然后数组每个元素的值表示这个元素的分数
- 要在这个多边形里面把一些点连起来,组成N-2个三角形
- 每个三角形的分数是a[i] * a[j] * a[k], 整体的分数是所有三角形的分数和
- 问,这个分数和的最小值是多少?
- 这个题目dp的特征也比较明显,但是dp的难度就在于如何定义状态, 从而可以把大问题转换成重叠子问题; 最近的感悟是输入是一维数组的dp通常会比较难,除非题目本身就是简单的一维动态规划, 因为如果输入是二维的,那么通常定义dp[i][j]的状态都会非常直接。 但是如果输入是一维的,通常需要自己想办法定义合理的状态, 形成重叠子问题,但是这个状态的定义有时候会比较难,摸不着套路。
- 比如之前做了312 Burst Balloons, http://www.noteanddata.com/leetcode-312-Burst-Balloons-java-solution-note.html
重点在于如果选择第一步的话,子问题在不停的变换(左右气球发生了变化),从而无法重叠, 但是如果选择最后一步的话, 左右的数都还没有被扎, 因为我们计算是从小距离到大距离开始计算,所以形成了重叠的子问题,这样就可以用动态规划的思路 - 又比如leetcode 1000 Minimum Cost to Merge Stones, http://www.noteanddata.com/leetcode-1000-Minimum-Cost-to-Merge-Stones-java-solution-note.html, 里面通过一个三维的状态数组, 构造了dp[i][j][c], 然后通过两个递推关系,计算了普通c个堆的构造, c-1和1堆,相当于切一刀; 另外把k个合并成一个
dp[i][j][c] = dp[i][t][c-1] + dp[t+1][j][1]
dp[i][j][1] = dp[i][j][k] + sum[i][j] - 和前面两个问题类似, 这里的动态规划也是需要寻找重叠子问题
这里假设dp[i][j]是从i到j的多边形的最小值。 那么,假设中间选一个点是k, 那么可以由i,j,k组成一个三角形,然后左边和右边就会形成重叠的子问题dp[i][k]和dp[k][j], 那么就有递推公式如下
dp[i][j] = min(dp[i][k] + dp[k][j] + a[i] * a[j] * a[k]) - 同时,我们做这个计算需要从小到大计算,所以需要循环距离从小到大, 也就是要计算dp[i][j]的时候,要保证dp[i][k]和dp[k][j]已经计算过了, 这样我们需要d=j-i 然后从小到大循环
- 对边界条件的思考需要自己推理一下, 这里需要防止溢出, 然后其他情况设置默认0就好了
public int minScoreTriangulation(int[] A) { int[][] dp = new int[A.length][A.length]; for(int d = 2; d < A.length; ++d) { for(int i = 0; i+d < A.length; ++i) { int j = i + d; int min = Integer.MAX_VALUE; for(int k = i+1; k < j; ++k) { min = Math.min(min, dp[i][k] + dp[k][j] + A[i] * A[k] * A[j]); } if(min != Integer.MAX_VALUE) { dp[i][j] = min; } } } return dp[0][A.length-1]; }https://blog.csdn.net/Sea_muxixi/article/details/89883775
题意:一个n多边形,如何分成n-2个三角形,使得每个三角形三个点乘积的和最小。
思路:区间dp。
dp[i][j]表示,将[i,j]的点组成的多边形的最小和。
k是(i,j)中的点。
这个多边形可以分成三个部分,多边形[i,k],多边形[k,j],三角形(i,j,k);
假设多边形[i,k],多边形[k,j]已知,遍历这个k,可以到这最小值。
然后可以将问题转化为子问题,求解多边形[i,k],多边形[k,j]的最小值。
有个小坑,这里要记忆化搜索,不然要超时。
https://www.cnblogs.com/seyjs/p/10955757.html
解题思路:这里推荐一本书《趣学算法》,里面有几个专题,讲解也非常有意思。本题对应书中的4.7章:最优三角剖分,解答如下图。

X. DFS+Cache: memoization DP
https://leetcode.com/problems/minimum-score-triangulation-of-polygon/discuss/286767/Java-memoization-DP-solution
https://leetcode.com/problems/minimum-score-triangulation-of-polygon/discuss/286767/Java-memoization-DP-solution
public int minScoreTriangulation(int[] A) {
return dfs(A, 0, A.length - 1, new Integer[A.length][A.length]);
}
int dfs(int[] A, int i, int j, Integer[][] memo) {
if (j < i + 2) return 0; // base case: you can't form a triangle with less than 3 points
if (memo[i][j] != null) return memo[i][j];
int res = Integer.MAX_VALUE;
for (int k = i + 1; k < j; ++k) {
res = Math.min(res, dfs(A, i, k, memo) + dfs(A, k, j, memo) + A[i] * A[k] * A[j]);
}
memo[i][j] = res;
return memo[i][j];
}


