LeetCode 1038 - Binary Search Tree to Greater Sum Tree

Related: same as LeetCode 538 - Convert BST to Greater Tree
https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/

Given the root of a binary search tree with distinct values, modify it so that every node has a new value equal to the sum of the values of the original tree that are greater than or equal to node.val.

As a reminder, a binary search tree is a tree that satisfies these constraints:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

Input: [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Note:

1. The number of nodes in the tree is between 1 and 100.
2. Each node will have value between 0 and 100.
3. The given tree is a binary search tree.

X. Reverse Order Traverse
https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/discuss/286725/JavaC%2B%2BPython-Revered-Inorder-Traversal

We need to do the work from biggest to smallest, right to left.
pre will record the previous value the we get, which the total sum of bigger values.
For each node, we update root.val with root.val + pre.

    int pre = 0;
    public TreeNode bstToGst(TreeNode root) {
        if (root.right != null) bstToGst(root.right);
        pre = root.val = pre + root.val;
        if (root.left != null) bstToGst(root.left);
        return root;
    }

https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/discuss/286906/Java-3-iterative-and-recursive-codes-w-comments-and-explanation.

Method 1:

Iterative version: use stack to pop out the nodes in reversed in order sequence.

Initially, use cur to point to the root,

1. push into Stack the right-most path of current subtree;
2. pop out a node, update sum and the node value;
3. point cur to the node's left child, if any;
   Repeat the above till the stack is empty and cur has no left child.

    public TreeNode bstToGst(TreeNode root) {
        Deque<TreeNode> stk = new ArrayDeque<>();
        TreeNode cur = root;
        int sum = 0;
        while (cur != null || !stk.isEmpty()) {
            while (cur != null) { // save right-most path of the current subtree
                stk.push(cur);
                cur = cur.right;
            }
            cur = stk.pop(); // pop out by reversed in-order.
            sum += cur.val; // update sum.
            cur.val = sum; // update node value.
            cur = cur.left; // move to left branch.
        }    
        return root;
    }

Analysis:

Time & space: O(n).

Method 2:

Recursive version: using a sum TreeNode (more safety) instead of an instance variable.

Obviously, sum updates its value by reversed in-order traversal of nodes.

    public TreeNode bstToGst(TreeNode root) {
        reversedInorder(root, new TreeNode(0));
        return root;
    }
    private void reversedInorder(TreeNode node, TreeNode sum) {
        if (node == null) { return; }
        reversedInorder(node.right, sum);
        sum.val += node.val;
        node.val = sum.val;
        reversedInorder(node.left, sum);
    }

Analysis:

Time: O(n), space: O(n) if considering recursion stack.

Method 3:

Iterative version.

Morris algorithm - for pictures and explanation in details please refer to here.

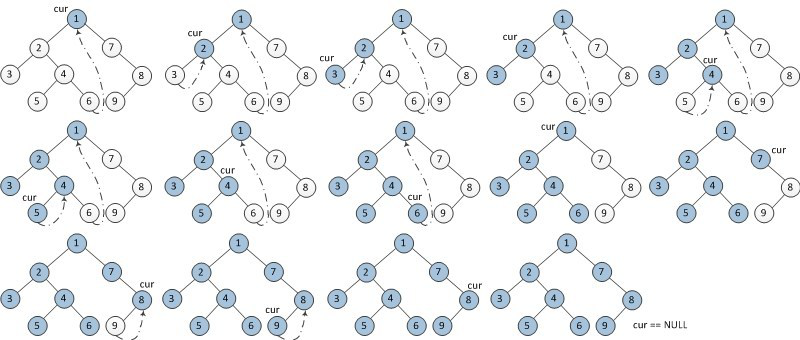
Note: typically the description of Morris algorithm is about in-order traversal, not reversed in-order. So I add comments for the following code to make beginners more comfortable, hopefully.

    public TreeNode convertBST(TreeNode root) {
        TreeNode cur = root;
        int sum = 0;
        while (cur != null) {
            if (cur.right != null) { // traverse right subtree.
                TreeNode leftMost = cur.right;
                while (leftMost.left != null && leftMost.left != cur) { // locate the left-most node of cur's right subtree.
                    leftMost = leftMost.left;
                }
                if (leftMost.left == null) { // never visit the left-most node yet.
                    leftMost.left = cur; // construct a way back to cur.
                    cur = cur.right; // explore right.
                }else { // visited leftMost already, which implies now on way back.
                    leftMost.left = null; // cut off the fabricated link.
                    sum += cur.val; // update sum.
                    cur.val = sum; // update node value.
                    cur = cur.left; // continue on way back.
                }
            }else { // no right child: 1) cur is the right-most of unvisited nodes; 2) must traverse left.
                sum += cur.val; // update sum.
                cur.val = sum; // update node value.
                cur = cur.left; // continue on way back.
            }
        }
        return root;
    }