LeetCode 1036 - Escape a Large Maze

https://xingxingpark.com/Leetcode-1036-Escape-a-Large-Maze/

In a 1 million by 1 million grid, the coordinates of each grid square are (x, y) with 0 <= x, y < 10^6.

We start at the source square and want to reach the target square. Each move, we can walk to a 4-directionally adjacent square in the grid that isn’t in the given list of blocked squares.

Return true if and only if it is possible to reach the target square through a sequence of moves.

Example 1:

Input: blocked = [[0,1],[1,0]], source = [0,0], target = [0,2]
Output: false
Explanation: The target square is inaccessible starting from the source square, because we can’t walk outside the grid.

Example 2:

Input: blocked = [], source = [0,0], target = [999999,999999]
Output: true
Explanation: Because there are no blocked cells, it’s possible to reach the target square.

Note:

1. 0 <= blocked.length <= 200
2. blocked[i].length == 2
3. 0 <= blocked[i][j] < 10^6
4. source.length == target.length == 2
5. 0 <= source[i][j], target[i][j] < 10^6
6. source != target

https://blog.baozitraining.org/2019/05/leetcode-solution-1036-escape-large-maze.html
At first, I am puzzled why this problem would be a hard one. It seems simply applying a BFS would get the answer. So here we go.
  

Brute force, simple BFS

Of course it will hit memory limit because I am allocating a 2-dimensional visited array. Assume boolean is 8 bit -> 1B, 1 Million * 1 Million = 1TB, OMG, immediately using a set instead.

P.S. fun fact, you can use this method to test how much memory leetcode allocate to this problem, you can use binary search and memory is around 300MB

However, this would start hitting Time Limit Exception. Now I begin to notice a few constrains, e.g., the block size is only 200 while the grid is 1M*1M. Simply going from source to target worst case would cause a timeout.

Next thought would be does it help if we sort the block array? While we are doing the BFS, if the block is already larger/smaller than the max/min of the block, we can early stop. However, this won't help if we simply place a block near the target. Also, this would be a nightmare to implement. 

Check block loops on source and target

Following the two hints, it would be natural to come up with this idea. Given such huge contrast between the block size (0,200) and the grid size (1M, 1M), all we need to do is to check if there is any loops built by block on source and target b/c if there is a loop, we cannot explore outside of the loop. However, notice if target and source are in the same loop, then we are fine.

There are two ways to early stop this loop checking. One way is to count the BFS steps, the other way is to follow the hints, given 200 blocks, what's the max area it can cover. Given the length 200, Fig 2 in the below graph can result in the largest area. Therefore, we can early terminate the BFS search once we covered more than 19900 blocks. (We can relax this a bit to 20000, doesn't matter)

• Fig 1 area = 100 * 100 = 10000
• Fig 2 area = 1 + 2 + 3 + ... + 199 = (1+199)*199/2 = 19900
• Fig 3 area = 1 * 200 = 200
• Fig 4 area = 790 (2*Pi*R = 100, thus R = 15.92, Pi * R^2 = 790 )

X. DFS
https://leetcode.com/problems/escape-a-large-maze/discuss/282889/My-Java-DFS-Solution-with-Some-Thoughts-(Triangle-v.s.-14-Circle-in-Pixels)

Note it states blocks.length <= 200. We can make use of it.

Find as many sqaures as possible from source and target individually. If both can reach more than a specified amount of squares (i.e. the largest closed area the block squares and the grid borders can form), it means they can both go beyond the blocks.

Code Updated (as pointed out by @andrew18):
---
You ignore the case that it can move directly from the source to target below the limit of number of moves. Consider the following case:
blocked: [[0,2],[1,0],[1,1]]
source: [0,0]; target: [0,1]

But how can we get the largest closed area? The largest one I can come up with is a 1/4 circle with its arc 200 in length. Then the area is 12,732 roughly.

However, we are facing a pixel problem. It's not a continous line, but is composed by pixels, which don't need to be adjacent to form a line (i.e. two pixels are positioned diagonally). In this case, the circle might not be the largest.

We can come up with another example: the 200-long line in exactly 45 degree which forms a triangle. The line is made up with 200 pixels but actually is 200 * sqrt(2) in length. The square is roughly (200 * sqrt(2)) * (200 * sqrt(2) / 2) / 2 = 20000. The number of accurate pixels is 1 + 2 + ... + 200 = 20100 (we can reduce 200 because they are blocks themselves XD. Then it's actuall 19900).

Let's see the 1/4 circle again. When we are trying to make a circle, we actually make some diagonally positioned pixels become adjacent. This will reduce the area at every step. So the triangle should be the larger one when the pixel count is fixed.

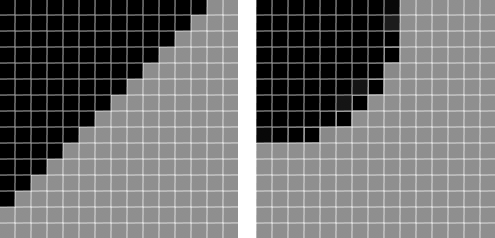
The following image shows the two examples when pixel count of the border is 13.

    final int MAX_VISIT = 20000;
 
    public boolean isEscapePossible(int[][] blocked, int[] source, int[] target) {
        Set<String> blockedSet = new HashSet<>();
        for (int[] point : blocked) {
            blockedSet.add(getKey(point));
        }
        return canVisit(blockedSet, source, getKey(target)) && canVisit(blockedSet, target, getKey(source));
    }
    
    String getKey(int[] point) {
        return point[0] + "," + point[1];
    }
    
    boolean canVisit(Set<String> blocked, int[] source, String targetKey) {
        Set<String> visited = new HashSet<>();
        dfs(blocked, source, targetKey, visited);
        return visited.size() >= MAX_VISIT || visited.contains(targetKey);
    }
    
    void dfs(Set<String> blocked, int[] curr, String targetKey, Set<String> visited) {
        int i = curr[0], j = curr[1];
        if (i < 0 || j < 0 || i >= 1e6 || j >= 1e6) { return; }
        
        String key = getKey(curr);
        if (blocked.contains(key)) { return; }
        if (visited.size() >= MAX_VISIT || visited.contains(targetKey)) { return; }
        
        if (visited.contains(key)) { return; }
        visited.add(key);
        
        for (int[] next : new int[][] {{i-1 ,j}, {i+1, j}, {i, j-1}, {i, j+1}}) {
            dfs(blocked, next, targetKey, visited);
        }
    }

https://leetcode.com/problems/escape-a-large-maze/discuss/282849/Python-BFS-and-DFS-Maximum-Blocked-19900

DFS:

    def isEscapePossible(self, blocked, source, target):
        blocked = set(map(tuple, blocked))

        def dfs(x, y, target, seen):
            if not (0 <= x < 10**6 and 0 <= y < 10**6) or (x, y) in blocked or (x, y) in seen: return False
            seen.add((x, y))
            if len(seen) > 20000 or [x, y] == target: return True
            return dfs(x + 1, y, target, seen) or \
                dfs(x - 1, y, target, seen) or \
                dfs(x, y + 1, target, seen) or \
                dfs(x, y - 1, target, seen)
        return dfs(source[0], source[1], target, set()) and dfs(target[0], target[1], source, set())

Python, BFS:

    def isEscapePossible(self, blocked, source, target):
        blocked = {tuple(p) for p in blocked}

        def bfs(source, target):
            bfs, seen = [source], {tuple(source)}
            for x0, y0 in bfs:
                for i, j in [[0, 1], [1, 0], [-1, 0], [0, -1]]:
                    x, y = x0 + i, y0 + j
                    if 0 <= x < 10**6 and 0 <= y < 10**6 and (x, y) not in seen and (x, y) not in blocked:
                        if [x, y] == target: return True
                        bfs.append([x, y])
                        seen.add((x, y))
                if len(bfs) == 20000: return True
            return False
        return bfs(source, target) and bfs(target, source)

https://blog.baozitraining.org/2019/05/leetcode-solution-1036-escape-large-maze.html

题目给我们一个1百万乘1百万的迷宫，同时告诉你其中一些点是阻隔的，不能通过。问你是否有一条通路可以从点source连接到target。

按照常规思路，我们首先想到的肯定是用DFS或者BFS的方法，从一个点开始，暴力搜索所有能到的点。但是，由于迷宫非常大，这样做的时间复杂度会达到O(10^12)，你提交的解法会 TLE。

我们回头仔细看题目给我们的Note, 发现blocked的长度是有限制的，最多不超过200。这能给我们带来启发。首先，两个点之所以不能联通，一定是因为被blocked中的点分隔开了。那意味着blocked中的点能将迷宫分割成两个部分，每个部分分别包含source和target中的一个点。而因为blocked的点数量不超过200，因此，它所能围城的面积也是有限制的。

我们可以将问题抽象成这样一个数学问题，在一个1000000 \* 1000000的矩形中，用一条长200的线，最多能围出多大的面积？这个问题可以用泛函的知识求解，这里不多做说明。但其实我们利用对称性可以知道，在任意一个角，围出一个弧长200的1/4圆就是最大的面积，也就是4/pi \* 10000。

知道了这个面积，我们只需要对source和target分别做两次BFS。每次BFS，我们设定所搜的次数不超过我们求出的这个最大面积。如果在这些点中找到了target或source,那自然说明有这样一条通路。否则：

1. 如果我们发现BFS在我们设定的搜索次数内，已经完成，那么说明source或者target处于被blocked点和迷宫边界构成的一个封闭区间内，不存在通路。
2. 如果BFS在设定的搜索次数内没有完成，说明并没有这样一个封闭区间能包裹住source或者target,那它们两个点一定是能够连通的。

下图给出target和source别阻隔时，可能的情况。(图片引子Discuss中2017111303的帖子)

1. 由于 block 列表的长度 m 最多只有 200，而网格却有 10^6 x 10^6。如果最终不能从起点到终点，则从起点或终点出发能到达的格子数量不超过 ${\frac{\mathrm{m^}}{\mathrm{2/}}}^2$；如果起点和终点都超过了这么多可达的格子，则一定能从起点到终点。（考虑极端情况，起点在角上，m 个点最多能封闭多少空间）
2. 基于此，我们先从起点开始 BFS，如果过程中遇到了终点或者可达格子个数超过了 m^2/2 个，则返回 true；然后同理再从终点开始 BFS，二者均返回 true 则最终返回 true。

时间复杂度

• 消耗的时间为 BFS 中的可达点数，最多为 $O({\mathrm{m^}}^2)$。

空间复杂度

• BFS 队列需要 $O({\mathrm{m^}}^2)$ 的空间。

https://www.acwing.com/solution/LeetCode/content/1695/

在一个 10^6 x 10^6 的网格中，每个网格块的坐标为 (x, y)，其中 0 <= x, y < 10^6。

我们从源方格 source 开始出发，意图赶往目标方格 target。每次移动，我们都可以走到网格中在四个方向上相邻的方格，只要该方格不在给出的封锁列表 blocked 上。

只有在可以通过一系列的移动到达目标方格时才返回 true。否则，返回 false。

样例

输入：blocked = [[0,1],[1,0]], source = [0,0], target = [0,2]
输出：false
解释：
从源方格无法到达目标方格，因为我们无法在网格中移动。

输入：blocked = [], source = [0,0], target = [999999,999999]
输出：true
解释：
因为没有方格被封锁，所以一定可以到达目标方格。




X. Video
Baozi Training Leetcode 1036 solution: Escape a Large Maze