https://leetcode.com/problems/matrix-cells-in-distance-order/
We are given a matrix with
R rows and C columns has cells with integer coordinates (r, c), where 0 <= r < R and 0 <= c < C.
Additionally, we are given a cell in that matrix with coordinates
(r0, c0).
Return the coordinates of all cells in the matrix, sorted by their distance from
(r0, c0) from smallest distance to largest distance. Here, the distance between two cells (r1, c1) and (r2, c2) is the Manhattan distance, |r1 - r2| + |c1 - c2|. (You may return the answer in any order that satisfies this condition.)
Example 1:
Input: R = 1, C = 2, r0 = 0, c0 = 0 Output: [[0,0],[0,1]] Explanation: The distances from (r0, c0) to other cells are: [0,1]
Example 2:
Input: R = 2, C = 2, r0 = 0, c0 = 1 Output: [[0,1],[0,0],[1,1],[1,0]] Explanation: The distances from (r0, c0) to other cells are: [0,1,1,2] The answer [[0,1],[1,1],[0,0],[1,0]] would also be accepted as correct.
Example 3:
Input: R = 2, C = 3, r0 = 1, c0 = 2 Output: [[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]] Explanation: The distances from (r0, c0) to other cells are: [0,1,1,2,2,3] There are other answers that would also be accepted as correct, such as [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]].
X. BFS
public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {
boolean[][] visited = new boolean[R][C];
int[][] result = new int[R * C][2];
int i = 0;
Queue<int[]> queue = new LinkedList<int[]>();
queue.offer(new int[]{r0, c0});
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int r = cell[0];
int c = cell[1];
if (r < 0 || r >= R || c < 0 || c >= C) {
continue;
}
if (visited[r][c]) {
continue;
}
result[i] = cell;
i++;
visited[r][c] = true;
queue.offer(new int[]{r, c - 1});
queue.offer(new int[]{r, c + 1});
queue.offer(new int[]{r - 1, c});
queue.offer(new int[]{r + 1, c});
}
return result;
}
X. O(n) Java Counting Sort (計數排序) Solution
The max distance is
R + C, and the result array's length is R * C. Since the distance is limited (generally, compared with the cell count), we can use Counting Sort (計數排序) to solve it efficiently.
Time complexity is
O(R * C), i.e. O(n).66 / 66 test cases passed.
Status: Accepted
Runtime: 4 ms
Memory Usage: 38.5 MB
class Solution {
public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {
int[] counter = new int[R + C + 1];
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
int dist = Math.abs(r - r0) + Math.abs(c - c0);
counter[dist + 1] += 1;
}
}
for (int i = 1; i < counter.length; i++) {
counter[i] += counter[i - 1];
}
int[][] ans = new int[R * C][];
for (int r = 0; r < R; r++) {
for (int c = 0; c < C; c++) {
int dist = Math.abs(r - r0) + Math.abs(c - c0);
ans[counter[dist]] = new int[] { r, c };
counter[dist]++;
}
}
return ans;
}X. http://www.noteanddata.com/leetcode-1030-Matrix-Cells-in-Distance-Order-java-solution-note.html
public int[][] allCellsDistOrder(int R, int C, int r0, int c0) { List<int[]> list = new ArrayList<>(); for(int i = 0; i < R; ++i) { for(int j = 0; j < C; ++j) { list.add(new int[]{i,j}); } } Collections.sort(list, new Comparator<int[]>() { public int compare(int[] a, int[] b) { return calcD(a) - calcD(b); } int calcD(int[] a) { return Math.abs(a[0]-r0) + Math.abs(a[1]-c0); } }); int[][] ret = new int[list.size()][2]; for(int i = 0; i < list.size(); ++i) { ret[i] = list.get(i); } return ret; }
https://leetcode.com/problems/matrix-cells-in-distance-order/discuss/278708/O(n)-with-picture
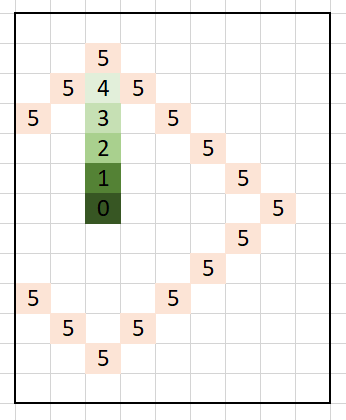
- Increment the distance from 0 till
R + C. - From our point, generate all points with the distance.
- Add valid poits (within our grid) to the result.
The image below demonstrates the generation of points with distance 5:
X. Sorting
https://leetcode.com/problems/matrix-cells-in-distance-order/discuss/278805/Java-Sorting-Solution
public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {
int[][] origin = new int[R * C][2];
for (int i = 0; i < R; i++) {
for (int j = 0; j < C; j++) {
origin[i * C + j] = new int[] {i, j};
}
}
Arrays.sort(origin, new Comparator<int[]>(){
public int compare(int[] a, int[] b) {
return Math.abs(a[0] - r0) + Math.abs(a[1] - c0)
- Math.abs(b[0] - r0) - Math.abs(b[1] - c0);
}
});
return origin;
}https://www.acwing.com/solution/LeetCode/content/1761/
给出 R 行 C 列的矩阵,其中的单元格的整数坐标为 (r, c),满足 0 <= r < R 且 0 <= c < C。
另外,我们在该矩阵中给出了一个坐标为 (r0, c0) 的单元格。
返回矩阵中的所有单元格的坐标,并按到 (r0, c0) 的距离从最小到最大的顺序排,其中,两单元格(r1, c1) 和 (r2, c2) 之间的距离是曼哈顿距离,|r1 - r2| + |c1 - c2|。(你可以按任何满足此条件的顺序返回答案。)
样例
示例 1:
输入:R = 1, C = 2, r0 = 0, c0 = 0
输出:[[0,0],[0,1]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1]
示例 2:
输入:R = 2, C = 2, r0 = 0, c0 = 1
输出:[[0,1],[0,0],[1,1],[1,0]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2]
[[0,1],[1,1],[0,0],[1,0]] 也会被视作正确答案。
示例 3:
输入:R = 2, C = 3, r0 = 1, c0 = 2
输出:[[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2,2,3]
其他满足题目要求的答案也会被视为正确,例如 [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]]。
提示:
1 <= R <= 100
1 <= C <= 100
0 <= r0 < R
0 <= c0 < C
算法1
(枚举+排序)
遍历矩阵,计算每个点到目标点的曼哈顿距离,将结果排序输出。
时间复杂度分析:n表示所有点的个数,排序需要时间复杂度
算法2
(BFS)
从目标点开始BFS,直接加入答案里,就是自动按照曼哈顿距离排序好的结果。
时间复杂度分析:n表示所有点的个数,需要时间复杂度