http://bookshadow.com/weblog/2016/07/07/leetcode-find-k-pairs-with-smallest-sums/
X. Use Priority Queue O(KlogK)
http://www.cnblogs.com/grandyang/p/5653127.html
这种方法我们从0循环到数组的个数和k之间的较小值,这样做的好处是如果k远小于数组个数时,我们不需要计算所有的数字对,而是最多计算k*k个数字对,然后将其都保存在res里,这时候我们给res排序,用我们自定义的比较器,就是和的比较,然后把比k多出的数字对删掉即可
https://discuss.leetcode.com/topic/50885/simple-java-o-klogk-solution-with-explanation
https://discuss.leetcode.com/topic/50529/java-9ms-heap-queue-solution-k-log-k
http://hehejun.blogspot.com/2017/11/leetcodefind-k-pairs-with-smallest-sums.html
如果我们将两个数组展开,可以得到一个2D的matrix。例如[1,2,3]和[1,1,2]。我们可以得到下图:
我们可以看出来,这个matrix从左向右,自上而下是递增的。假设有m行,n列,就可以看做m个长度为n的sorted list,那么这个问题也就转变为merge m sorted list and get first k element,那么很明显我们就可以用priority queue来解。我们先把[0, 0]加入优先队列,每次从队列中取出最小的,如果其下边和右边还有元素就将其推入优先队列,直到得到k个元素。循环只有k次,每次我们取出一个最多推入两个,优先队列初始长度为1,所以队列长度<= k。时间按复杂度O(k),空间复杂度O(klog2k)
https://segmentfault.com/a/1190000008309330
You are given two integer arrays nums1 and nums2 sorted in ascending order and an integer k.
Define a pair (u,v) which consists of one element from the first array and one element from the second array.
Find the k pairs (u1,v1),(u2,v2) ...(uk,vk) with the smallest sums.
Example 1:
Example 2:
Example 3:
给定两个递增有序的整数数组nums1和nums2,以及一个整数k。
定义一个数对(u, v),包含第一个数组中的一个元素以及第二个数组中的一个元素。
寻找和最小的k个这样的数对(u1,v1),(u2,v2) ...(uk,vk)。
https://discuss.leetcode.com/topic/50450/slow-1-liner-to-fast-solutionsX. Use Priority Queue O(KlogK)
http://www.cnblogs.com/grandyang/p/5653127.html
这种方法我们从0循环到数组的个数和k之间的较小值,这样做的好处是如果k远小于数组个数时,我们不需要计算所有的数字对,而是最多计算k*k个数字对,然后将其都保存在res里,这时候我们给res排序,用我们自定义的比较器,就是和的比较,然后把比k多出的数字对删掉即可
https://discuss.leetcode.com/topic/50885/simple-java-o-klogk-solution-with-explanation
https://discuss.leetcode.com/topic/50529/java-9ms-heap-queue-solution-k-log-k
Basic idea: Use min_heap to keep track on next minimum pair sum, and we only need to maintain K possible candidates in the data structure.
Some observations: For every numbers in nums1, its best partner(yields min sum) always strats from nums2[0] since arrays are all sorted; And for a specific number in nums1, its next candidate sould be [this specific number] + nums2[current_associated_index + 1], unless out of boundary;)
Here is a simple example demonstrate how this algorithm works.
The run time complexity is O(kLogk) since que.size <= k and we do at most k loop.
public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<int[]> que = new PriorityQueue<>((a,b)->a[0]+a[1]-b[0]-b[1]);
List<int[]> res = new ArrayList<>();
if(nums1.length==0 || nums2.length==0 || k==0) return res;
for(int i=0; i<nums1.length && i<k; i++) que.offer(new int[]{nums1[i], nums2[0], 0});
while(k-- > 0 && !que.isEmpty()){
int[] cur = que.poll();
res.add(new int[]{cur[0], cur[1]});
if(cur[2] == nums2.length-1) continue;
que.offer(new int[]{cur[0],nums2[cur[2]+1], cur[2]+1});
}
return res;
}http://hehejun.blogspot.com/2017/11/leetcodefind-k-pairs-with-smallest-sums.html
另外一点,如果这道题不是求前k个,而是求第k个,我们还可以用值域的二分法来做。例如,Kth Smallest Element in Sorted Array, Find Kth Smallest Pair Distance
如果我们将两个数组展开,可以得到一个2D的matrix。例如[1,2,3]和[1,1,2]。我们可以得到下图:
我们可以看出来,这个matrix从左向右,自上而下是递增的。假设有m行,n列,就可以看做m个长度为n的sorted list,那么这个问题也就转变为merge m sorted list and get first k element,那么很明显我们就可以用priority queue来解。我们先把[0, 0]加入优先队列,每次从队列中取出最小的,如果其下边和右边还有元素就将其推入优先队列,直到得到k个元素。循环只有k次,每次我们取出一个最多推入两个,优先队列初始长度为1,所以队列长度<= k。时间按复杂度O(k),空间复杂度O(klog2k)
https://segmentfault.com/a/1190000008309330
greedy: 先把一组x里面和另外一组y最小元素的组合放进heap,然后每次poll出和最小的,同时放进去有可能成为第二小的组合,即当前y元素的下一个和x元素的组合。
https://discuss.leetcode.com/topic/51163/java-priorityqueue-9ms-without-helper-class public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) {
List<int[]> res = new LinkedList<>();
if(nums1==null || nums1.length==0 || nums2==null || nums2.length==0) {
return res;
}
// index pair
PriorityQueue<int[]> minQ = new PriorityQueue<>(new Comparator<int[]>(){
public int compare(int[] pair1, int[] pair2) {
return (nums1[pair1[0]]+nums2[pair1[1]])-(nums1[pair2[0]]+nums2[pair2[1]]);
}
});
minQ.offer(new int[]{0, 0});
while (k>0 && !minQ.isEmpty()) {
int[] pair=minQ.poll();
int i = pair[0];
int j = pair[1];
res.add(new int[]{nums1[i], nums2[j]});
k--;
if(j+1<nums2.length) {
minQ.offer(new int[]{i, j+1});
}
if(j==0 && i+1<nums1.length){
minQ.offer(new int[] {i+1, 0}); //\\
}
}
return res;
}
We can use a heap to store
k candidate pairs. For every numbers in nums1, its best partner (yields min sum) always starts from nums2[0] since arrays are all sorted; And for a specific number in nums1, its next candidate should be [this specific number] + nums2[current_partner_index + 1], unless out of boundary for nums2. public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) {
k = Math.min(nums1.length * nums2.length, k);
List<int[]> res = new ArrayList<>(k);
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> (a[0] + a[1]) - (b[0] + b[1]));
int l = 0, r = 0;
for(int i = 0; i < Math.min(k, nums1.length); i++)
q.offer(new int[]{nums1[i], nums2[0], 0});
for(int i = 0; i < k; i++) {
int[] arr = q.poll();
res.add(new int[]{arr[0], arr[1]});
if(arr[2] < nums2.length - 1)
q.offer(new int[]{arr[0], nums2[++arr[2]], arr[2]});
}
return res;
}
X. O(k) solution
https://discuss.leetcode.com/topic/50647/9ms-java-solution-with-explanation/2
https://discuss.leetcode.com/topic/52953/share-my-solution-which-beat-96-42
the basic idea is using a priority queue to store the candidates and pop them out in ascending order.
But, actually you don't need to store all of the pairs at the beginning, do you?
But, actually you don't need to store all of the pairs at the beginning, do you?
Imagine a matrix:
a1 a2 a3
a4 a5 a6
a7 a8 a9
The number in m[i][j] refers to the sum of nums1[i] + nums[j].
When you pop the value in m[0][1] (which is "a2"), actually you only need to put candidates m[1][1] ("a3") and m[0][2] ("a5") to the queue. And at this moment you don't need to care any other candidate.
In this way, the priority queue can be quite short comparing to putting all the pairs in the beginning.
Ok, now is there any thing you need to pay attention to? Yes, please notice there might be duplicates.
"a2" will lead to "a3" and "a5", while "a4" will lead to "a5" and "a7", thus "a5" will be a dup.
"a2" will lead to "a3" and "a5", while "a4" will lead to "a5" and "a7", thus "a5" will be a dup.
How to handle this?
I don't have a very good solution. my current one is to add the first column at the beginning, then each time you pop one item, you just add the one on the right and ignore the one below (since it will be someone else's right unless it's in the first column).
assuming nums1.length == nums2.length == n. time complexity should be klogn. The PQ's maximum size should be a linear function of n, not n^2. Image it is a regular bfs using a queue. The maximum size of PQ happens when all elements are along the diagonal line of matrix, which is sqrt2*n.
-- Uses too much space: visited[][] - use HashSet
I don't have a very good solution. my current one is to add the first column at the beginning, then each time you pop one item, you just add the one on the right and ignore the one below (since it will be someone else's right unless it's in the first column).
use a matrix to represent all combination of pairs from nums1 and nums2. Do a bfs from [0][0]. However, use a PriorityQueue instead of regular queue.
assuming nums1.length == nums2.length == n. time complexity should be klogn. The PQ's maximum size should be a linear function of n, not n^2. Image it is a regular bfs using a queue. The maximum size of PQ happens when all elements are along the diagonal line of matrix, which is sqrt2*n.
-- Uses too much space: visited[][] - use HashSet
final int[][] neighbors = {{0, 1}, {1, 0}};
public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) {
List<int[]> list = new ArrayList<>();
if (nums1 == null || nums2 == null || nums1.length == 0 || nums2.length == 0 || k == 0) {
return list;
}
int m = nums1.length, n = nums2.length;
boolean[][] visited = new boolean[m][n];
Queue<Pair> minHeap = new PriorityQueue<>();
minHeap.offer(new Pair(0, 0, nums1[0] + nums2[0]));
visited[0][0] = true;
while (k > 0 && !minHeap.isEmpty()) {
Pair min = minHeap.poll();
list.add(new int[] {nums1[min.row], nums2[min.col]});
k--;
for (int[] neighbor : neighbors) {
int row1 = min.row + neighbor[0];
int col1 = min.col + neighbor[1];
if (row1 < 0 || row1 == m || col1 < 0 || col1 == n || visited[row1][col1]) {
continue;
}
visited[row1][col1] = true;
minHeap.offer(new Pair(row1, col1, nums1[row1] + nums2[col1]));
}
}
return list;
}
}
class Pair implements Comparable<Pair> {
int row;
int col;
int value;
Pair(int row, int col, int value) {
this.row = row;
this.col = col;
this.value = value;
}
public int compareTo(Pair other) {
return value - other.value;
}
}public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k)
{
List<int[]> result = new LinkedList<int[]>();
if (nums1 == null || nums2 == null || nums1.length == 0 || nums2.length == 0 || k == 0) return result;
PriorityQueue<Triple> queue = new PriorityQueue<Triple>(nums1.length, new Comparator<Triple>() {
public int compare(Triple a, Triple b)
{
return Integer.compare(a.val, b.val);
}
});
// add the first column
for (int i=0; i<nums1.length; i++)
{
queue.add(new Triple(nums1[i]+nums2[0], i, 0));
}
while (k-- > 0 && !queue.isEmpty())
{
Triple current = queue.poll();
result.add(new int[]{nums1[current.one], nums2[current.two]});
// if the current one has a right candidate, add it to the queue.
if (current.two+1 < nums2.length)
queue.add(new Triple(nums1[current.one]+nums2[current.two+1], current.one, current.two+1));
}
return result;
}
// Triple is used to store the sum, the index in nums1 and the index in nums2.
class Triple
{
int val;
int one;
int two;
Triple (int val, int one, int two)
{
this.val = val;
this.one = one;
this.two = two;
}
}array1 = (0,0),(0,1),(0,2),....
array2 = (1,0),(1,1),(1,2),....
....
arrayk = (k-1,0),(k-1,1),(k-1,2),....
So, each time when an array is chosen having the smallest sum, you only move its index to next one of this array.
https://discuss.leetcode.com/topic/53380/o-k-solution
Now that I can find the kth smallest element in a sorted n×n matrix in time O(min(n, k)), I can finally solve this problem in O(k).
The idea:
- If
nums1ornums2are larger thank, shrink them to sizek. - Build a virtual matrix of the pair sums, i.e.,
matrix[i][j] = nums1[i] + nums2[j]. Make it a square matrix by padding with "infinity" if necessary. With "virtual" I mean its entries will be computed on the fly, and only those that are needed. This is necessary to stay within O(k) time. - Find the kth smallest sum
kthSumby using that other algorithm. - Use a saddleback search variation to discount the pairs with sum smaller than
kthSum. After this,ktells how many pairs we need whose sum equalskthSum. - Collect all pairs with sum smaller than
kthSumas well askpairs whose sum equalskthSum.
Each of those steps only takes O(k) time.
The code (minus the code for kthSmallest, which you can copy verbatim from my solution to the other problem):
def kSmallestPairs(self, nums1_, nums2_, k):
# Use at most the first k of each, then get the sizes.
nums1 = nums1_[:k]
nums2 = nums2_[:k]
m, n = len(nums1), len(nums2)
# Gotta Catch 'Em All?
if k >= m * n:
return [[a, b] for a in nums1 for b in nums2]
# Build a virtual matrix.
N, inf = max(m, n), float('inf')
class Row:
def __init__(self, i):
self.i = i
def __getitem__(self, j):
return nums1[self.i] + nums2[j] if self.i < m and j < n else inf
matrix = map(Row, range(N))
# Get the k-th sum.
kthSum = self.kthSmallest(matrix, k)
# Discount the pairs with sum smaller than the k-th.
j = min(k, n)
for a in nums1:
while j and a + nums2[j-1] >= kthSum:
j -= 1
k -= j
# Collect and return the pairs.
pairs = []
for a in nums1:
for b in nums2:
if a + b >= kthSum + (k > 0):
break
pairs.append([a, b])
k -= a + b == kthSum
return pairs
def kthSmallest(self, matrix, k):
# copy & paste from https://discuss.leetcode.com/topic/53126/o-n-from-paper-yes-o-rowsX. O(KlogK)
Don't use PQ
https://discuss.leetcode.com/topic/50527/java-10ms-solution-no-priority-queue
https://discuss.leetcode.com/topic/50632/java-priority-queue-or-without-priority-queue
- With Priority Queue. Scan [k+1, 2K] pair. Heap size is [2, k]. O(klogk) time, O(k) space
- Without Priority Queue. O(N^2) time, O(1) space
用最小堆保存遍历过程中的pairs。
当遍历到(i,j)时,继续往下遍历,相邻的结点是(i+1,j),(i,j+1)
因为是有序数组,这两个pair是较小的,加入堆中。
public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) {
List<int[]> res = new ArrayList<int[]>();
boolean visit[][] = new boolean[nums1.length][nums2.length];
Queue<int[]> heap = new PriorityQueue<int[]>(new Comparator<int[]>(){
public int compare(int[] i, int[] j) {
return (nums1[i[0]] + nums2[i[1]] -( nums1[j[0]] + nums2[j[1]]));
}
});
heap.add(new int[] { 0, 0 });
visit[0][0] = true;
while (!heap.isEmpty() && res.size() < k) {
int d[] = heap.poll();
res.add(new int[] { nums1[d[0]], nums2[d[1]] });
if (d[1] + 1 < nums2.length && visit[d[0]][d[1] + 1] == false) {
heap.add(new int[] { d[0], d[1] + 1 });
visit[d[0]][d[1] + 1] = true;
}
if (d[0] + 1 < nums1.length && visit[d[0]+1][d[1]] == false) {
heap.add(new int[] { d[0]+1, d[1]});
visit[d[0]+1][d[1]] = true;
}
}
return res;
}
最直接的思路是把全部的数都组合一下,然后维护一个大小为k的最大堆 这样复杂度O(m*n*logk)
其实还可以维护一个最小堆,每次取出堆顶的元素,然后把该元素相邻结点加入进去。这样能保证最小。
struct Order {
int sum;
int index1, index2;
Order(int a, int b, int sum) : index1(a), index2(b), sum(sum) {}
bool operator < (const Order& b) const {
return sum > b.sum;
}
};
int dx[] = { 1,0 };
int dy[] = { 0,1 };
class Solution {
public:
vector<pair<int, int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
vector<pair<int, int>> ans;
if (nums1.empty() || nums2.empty()) return ans;
int n = nums1.size(), m = nums2.size();
vector<vector<bool>> vis(n, vector<bool>(m, false));
priority_queue<Order> q;
q.push(Order(0, 0, nums1[0] + nums1[1]));
vis[0][0] = true;
while (k > 0 && !q.empty()) {
Order cur = q.top();
q.pop();
k--;
int x = cur.index1, y = cur.index2;
ans.push_back(make_pair(nums1[x], nums2[y]));
for (int i = 0; i < 2; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx < n && ny < m && !vis[nx][ny]) {
q.push(Order(nx, ny, nums1[nx] + nums2[ny]));
vis[nx][ny] = true;
}
}
}
return ans;
}
};
http://www.2cto.com/px/201607/524030.htmlpublic ListkSmallestPairs(int[] nums1, int[] nums2, int k) { List res = new ArrayList (); boolean visit[][] = new boolean[nums1.length][nums2.length]; Queue heap = new PriorityQueue (new Comparator (){ public int compare(int[] i, int[] j) { return (nums1[i[0]] + nums2[i[1]] -( nums1[j[0]] + nums2[j[1]])); } }); heap.add(new int[] { 0, 0 }); visit[0][0] = true; while (!heap.isEmpty() && res.size() < k) { int d[] = heap.poll(); res.add(new int[] { nums1[d[0]], nums2[d[1]] }); if (d[1] + 1 < nums2.length && visit[d[0]][d[1] + 1] == false) { heap.add(new int[] { d[0], d[1] + 1 }); visit[d[0]][d[1] + 1] = true; } if (d[0] + 1 < nums1.length && visit[d[0]+1][d[1]] == false) { heap.add(new int[] { d[0]+1, d[1]}); visit[d[0]+1][d[1]] = true; } } return res; }
def kSmallestPairs(self, nums1, nums2, k): queue = [] def push(i, j): if i < len(nums1) and j < len(nums2): heapq.heappush(queue, [nums1[i] + nums2[j], i, j]) push(0, 0) pairs = [] while queue and len(pairs) < k: _, i, j = heapq.heappop(queue) pairs.append([nums1[i], nums2[j]]) push(i, j + 1) if j == 0: push(i + 1, 0) return pairs
X. http://www.cnblogs.com/lettuan/p/6207659.html
本题的特点在于两个list nums1和nums2都是已经排序好的。本题如果把所有的(i, j)组合都排序出来,再取其中最小的K个。其实靠后的很多组合根本用不到,所以效率较低,会导致算法超时。为了简便,把nums1和nums2里面的元素写成A1,A2,...,A5, B1,...,B5. 维护一个最小堆。并逐渐往里面push and pop元素。
注意以下几点:1. 如果(Ai, Bj)大于堆顶的元素,那么没有必要把(Ai, Bj)和它之后的元素Push进堆。2. 为了便于管理,解法里其实只维护了一个指针idx2。如果 (A1,B[idx2])已经小于堆顶的元素,那么就把(A1,B[idx2]),...,(A5,B[idx2])全都推到堆里面。
第〇步,把一个最大元素放进堆。注意这一步很重要,否则可能会出现(A1,B2)大于所有(Ai,B1)的情况,也就是第二步中红色箭头大于蓝色箭头的情况始终不会出现,那么如果k足够大,就可能会出现pop一个空堆的bug。
第一步 把所有的(A1,B1),..., (A5,B1)推入堆。也就是把所有的黑色箭头连接的pair都放到堆里。
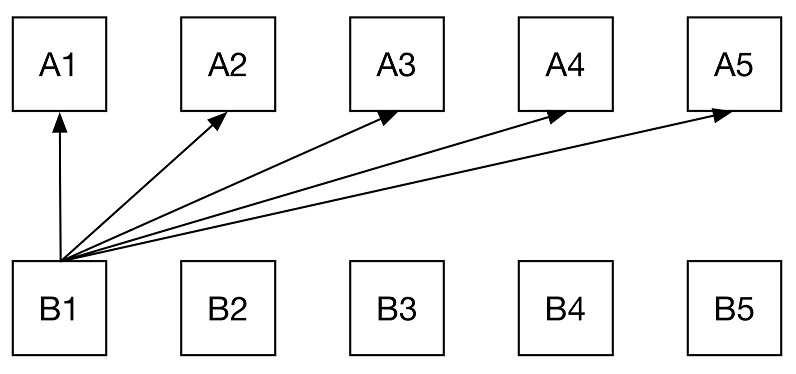
然后在逐个pop堆顶的元素。直到出现(A1,B2)小于堆顶的情况 (红色箭头小于蓝色箭头)。如果出现,把所有的(A1,B2),...,(A5,B2)放进堆。恢复pop堆顶元素,并且开始监视下一个红色箭头(A1,B3)是否小于堆顶的元素。
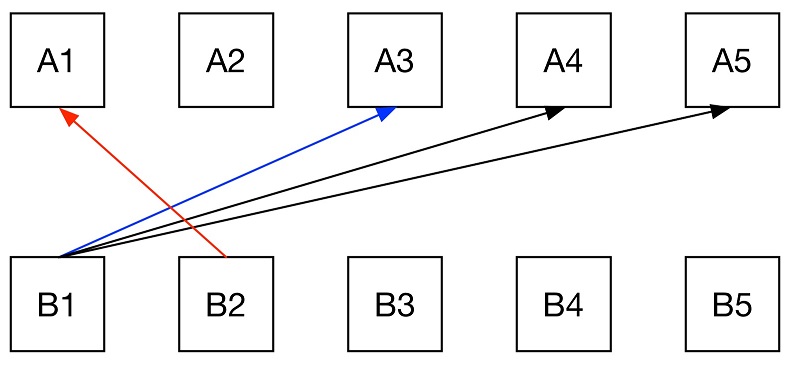
1 def kSmallestPairs(nums1, nums2, k): 8 ans = [] 9 heap = [(0x7FFFFFFF, None, None)] 10 size1, size2 = len(nums1), len(nums2) 11 idx2 = 0 12 while len(ans) < min(k, size1 * size2): 13 if idx2 < size2: 14 sum, i, j = heap[0] 15 if nums2[idx2] + nums1[0] < sum: 16 for idx1 in range(size1): 17 heapq.heappush(heap, (nums1[idx1] + nums2[idx2], idx1, idx2)) 18 idx2 += 1 19 sum, i, j = heapq.heappop(heap) 20 ans.append((nums1[i], nums2[j])) 21 return ans
This problem is similar to Super Ugly Number. The basic idea is using an array to track the index of the next element in the other array.
The best way to understand this solution is using an example such as nums1={1,3,11} and nums2={2,4,8}.
还有一种不需要产生所有的组合, 这种思想有点像寻找第k个丑数, 记录一下nums1中每个数对应nums2中组合的位置. 然后每次找到能够产生最小的组合即可.http://blog.csdn.net/qq508618087/article/details/51864835
这种思想有点像寻找第k个丑数, 记录一下nums1中每个数对应nums2中组合的位置. 然后每次找到能够产生最小的组合即可.
X. https://discuss.leetcode.com/topic/50527/java-10ms-solution-no-priority-queue/2 TODO
X. Brute Force
http://www.cnblogs.com/grandyang/p/5653127.html
https://discuss.leetcode.com/topic/50514/java-brute-force-solution-with-priorityqueue-150ms
Time Complexity: O(mnlogK)
Space: O(K)
Space: O(K)
vector<pair<int, int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) { vector<pair<int, int>> res; for (int i = 0; i < min((int)nums1.size(), k); ++i) { for (int j = 0; j < min((int)nums2.size(), k); ++j) { res.push_back({nums1[i], nums2[j]}); } } sort(res.begin(), res.end(), [](pair<int, int> &a, pair<int, int> &b){return a.first + a.second < b.first + b.second;}); if (res.size() > k) res.erase(res.begin() + k, res.end()); return res; }X.
http://www.cnblogs.com/grandyang/p/5653127.html
vector<pair<int, int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) { vector<pair<int, int>> res; multimap<int, pair<int, int>> m; for (int i = 0; i < min((int)nums1.size(), k); ++i) { for (int j = 0; j < min((int)nums2.size(), k); ++j) { m.insert({nums1[i] + nums2[j], {nums1[i], nums2[j]}}); } } for (auto it = m.begin(); it != m.end(); ++it) { res.push_back(it->second); if (--k <= 0) return res; } return res; }
https://www.geeksforgeeks.org/find-k-pairs-smallest-sums-two-arrays/
Time Complexity : O(k*n1)
http://www.voidcn.com/blog/niuooniuoo/article/p-6091497.html
https://discuss.leetcode.com/topic/50450/slow-1-liner-to-fast-solutions
TODO
https://discuss.leetcode.com/topic/53126/o-n-from-paper-yes-o-rows
X. Follow up:
if there are more arrays then 2, how can we use this approach to solve?

