hihocoder 1154 Spring Outing - Pat - 博客园
You class are planning for a spring outing. people are voting for a destination out of candidate places.
The voting progress is below:
First the class vote for the first candidate place. If more than half of the class agreed on the place, the place is selected. The voting ends.
Otherwise they vote for the second candidate place. If more than half of the class agreed on the place, the place is selected. The voting ends.
Otherwise they vote for the third candidate place in the same way and go on.
If no place is selected at last there will be no spring outing and everybody stays at home.
Before the voting, the Chief Entertainment Officer did a survey, found out every one's preference which can be represented as a permutation of . ( is for staying at home.) For example, when , preference "" means that the first place is his first choice, staying at home is the second choice, the second place is the third choice and the third place is the last choice.
The Chief Entertainment Officer sends the survey results to the class. So everybody knows the others' preferences. Everybody wants his more prefered place to be selected. And they are very smart, they always choose the optimal strategy in the voting progress to achieve his goal.
Can you predict which place will be selected?
The next lines each contain a permutation of ~, representing someone's preference.
For 40% of the data,
For 100% of the data,
http://hihocoder.com/discuss/question/2819/
Read full article from hihocoder 1154 Spring Outing - Pat - 博客园
You class are planning for a spring outing. people are voting for a destination out of candidate places.
The voting progress is below:
First the class vote for the first candidate place. If more than half of the class agreed on the place, the place is selected. The voting ends.
Otherwise they vote for the second candidate place. If more than half of the class agreed on the place, the place is selected. The voting ends.
Otherwise they vote for the third candidate place in the same way and go on.
If no place is selected at last there will be no spring outing and everybody stays at home.
Before the voting, the Chief Entertainment Officer did a survey, found out every one's preference which can be represented as a permutation of . ( is for staying at home.) For example, when , preference "" means that the first place is his first choice, staying at home is the second choice, the second place is the third choice and the third place is the last choice.
The Chief Entertainment Officer sends the survey results to the class. So everybody knows the others' preferences. Everybody wants his more prefered place to be selected. And they are very smart, they always choose the optimal strategy in the voting progress to achieve his goal.
Can you predict which place will be selected?
输入
The first line contains two integers, and , the number of people in your class and the number of candidate places.The next lines each contain a permutation of ~, representing someone's preference.
For 40% of the data,
For 100% of the data,
输出
Output the selected place. Or "otaku" without quotes if no place is selected.样例提示
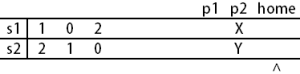
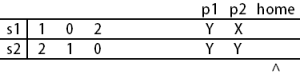
In the sample case, if the second peoson vote against the first place, no place would be selected finally because the first person must vote against the second place for his own interest. Considering staying at home is a worse choice than the first place, the second person's optimal strategy is voting for the first place. So the first place will be selected.- 样例输入
- 2 2 1 0 2 2 1 0
- 样例输出
- 1
对于每一个地点,我们可以把人分成三类:
1、当前地点在这类人的眼里优先级是最高的;
2、当前地点在这类人的眼里优先级不是最高,但是比蹲在家里好;
3、宁愿蹲家里也不去当前地点的人;
1、当前地点在这类人的眼里优先级是最高的;
2、当前地点在这类人的眼里优先级不是最高,但是比蹲在家里好;
3、宁愿蹲家里也不去当前地点的人;
那么当给某个地点投票时,1、3类人的意愿是很明确的,优先级最高的肯定投同意,家里蹲的肯定投反对,剩下的2类人就是要考虑投与不投的,而这类人考虑的因素就是后面能否确定得到【而不是存在】更好的选择。并且我们还知道,如果某个地点的优先级比0还低的话那么这个地点也是肯定被投反对的。
所以剩下的问题就是怎样去求“后面能否确定得到【而不是存在】更好的选择”。先模拟一下样例的选择过程(从后往前推,到达最后一个地点进行投票时,结果是确定的,因为这时只有两个选择了):
1、当对p2投票时,学生s1明显选择家里蹲也不会选择去地点p2
2、因此我们知道了对p2的投票结果,回到p1,如果2投X票的话,那么会造成家里蹲的结果。
由此,我们可以知道,假设某个地点pk一定会通过投票,那么对于pn(n > k)就是不可能被选择到的,因为到达pk时投票结束。
那么对于当前点pi(i < k)的投票,2类人要考虑的是:对于 pk 点,如果pk 优先级高于pi ,那么必定对pi 投反对票,因为过了pi点,下一个会被赞同的点必然是pk点,根据题意每个人尽量想去优先级高的地点。
例如上面的选择过程,对p1进行投票时,我们知道过了p1下一个pk点是home,而对学生s2来说,p1的优先级是高于home的,并且没有其它优先级高于p1的可达点(当然,有的话home就不是pk点了)
而对于最后一个点的投票是确定的,所以从最后的点往前搜索,记录pk点,最后得到的pk点就是问题所求。
https://glatue.wordpress.com/2016/02/25/hihocoder-1154-spring-outing/
N个人选K个地点,每个人都有自己的优先级,还可以选择在家。题目是每个人都事先知道了其他人的选择优先级,问大家都“非常聪明”的情况下,应该怎么选?
此类“参与人都非常聪明”的问题,关键是要找出“不得不”的值。比如Nim游戏,一个人选择了一个值,另一个人必定会根据这个值选一个合适的值,胜负在开始就已经决定了,无论输者选什么,胜者都能够选择一个值来应对输者的选择,使得游戏永远都是自己胜。
此题也要找到这种确定的“不得不”的值。
题解这么说:
假设我们已经进行到了最后一轮,需要对地点m进行投票。这时每个人都知道:如果地点m没有超过半数,那么最终的结果就是宅在家里(地点0)。于是所有认为m比0好的人必然投赞成票,而所有认为0比m好的人必然投反对票。所以如果进入到了最后一轮,那么最终选出的地点是确定的,我们不妨记为result[m]。(如果赞成票多于反对票,那么result[m]=m,否则result[m]=0。对于确定的输入数据,result[m]是唯一确定的。)
此类“参与人都非常聪明”的问题,关键是要找出“不得不”的值。比如Nim游戏,一个人选择了一个值,另一个人必定会根据这个值选一个合适的值,胜负在开始就已经决定了,无论输者选什么,胜者都能够选择一个值来应对输者的选择,使得游戏永远都是自己胜。
此题也要找到这种确定的“不得不”的值。
题解这么说:
假设我们已经进行到了最后一轮,需要对地点m进行投票。这时每个人都知道:如果地点m没有超过半数,那么最终的结果就是宅在家里(地点0)。于是所有认为m比0好的人必然投赞成票,而所有认为0比m好的人必然投反对票。所以如果进入到了最后一轮,那么最终选出的地点是确定的,我们不妨记为result[m]。(如果赞成票多于反对票,那么result[m]=m,否则result[m]=0。对于确定的输入数据,result[m]是唯一确定的。)
现在假设我们进行到倒数第二轮,需要对地点m-1进行投票。根据以上分析,这时每个人都知道:如果地点m-1没有超过半数,那么最终的结果就是result[m]。于是所有认为m-1比result[m]好的人必然投赞成票,而所有认为result[m]比m-1好的人必然投反对票。最终选出的地点也是确定的,我们不妨记为result[m-1]。
以此类推,我们可以求得result[m-2], result[m-3], …, result[2], result[1]。其中result[1]就是本题的答案。
int N, K;int choose(vector<vector<int>> &ranks, int now, int prev){ int cnt = 0; for (int i = 0; i < N; i++) cnt += (ranks[i][now] < ranks[i][prev]); return cnt * 2 <= N ? prev : now;}int main(){ //freopen("t.txt", "r", stdin); cin >> N >> K; vector<vector<int>> ranks(N, vector<int>(K + 1, 0)); for (int i = 0; i < N; i++) for (int j = 0; j < K + 1; j++) { int x; scanf("%d", &x); ranks[i][x] = j; } vector<int> result(K + 2); result[K + 1] = 0; for (int i = K; i >= 1; i--) result[i] = choose(ranks, i, result[i + 1]); if (0 == result[1]) cout << "otaku" << endl; else cout << result[1] << endl; return 0;} |
result = 0
For i = m .. 1
vote = 0
For j = 1 .. n
If (rank[j][i] < rank[j][result]) Then
vote = vote + 1
End If
End For
If (vote > n / 2) Then
result = i
End If
End For
其中
rank[j][i]表示表示第j个人心中,地点i的排名,值越小越靠前;同时把result数组简化为一个变量(这是由于计算result[i]时只需要result[i+1]的值)。