https://en.wikipedia.org/wiki/Weighted_median
For distinct elements
distinct elements  with positive weights
with positive weights  such that
such that  , the weighted median is the element
, the weighted median is the element 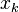 satisfying:
satisfying:  and
and 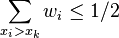
http://blog.csdn.net/sr_19930829/article/details/40793715
https://en.wikipedia.org/wiki/Weighted_median
Weighted median can be computed by sorting the set of numbers and finding the smallest numbers which sums to half the weight of total weight. This algorithm takes time. There is a better approach to find weighted median using a modified selection algorithm
time. There is a better approach to find weighted median using a modified selection algorithm

https://github.com/gzc/CLRS/blob/master/C09-Medians-and-Order-Statistics/problems/weighted_median.py
http://clrs.skanev.com/09/problems/02.html
For
 distinct elements
distinct elements  with positive weights
with positive weights  such that
such that  , the weighted median is the element
, the weighted median is the element 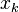 satisfying:
satisfying:  and
and 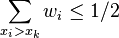
http://blog.csdn.net/sr_19930829/article/details/40793715
For n elements x1, x2, ..., xn with positive integer weights w1, w2, ..., wn. The weighted median is the element xk satisfying
 and
and  , S indicates
, S indicates 
Can you compute the weighted median in O(n) worst-case?
输入
There are several test cases. For each case, the first line contains one integer n(1 ≤ n ≤ 10^7) — the number of elements in the sequence. The following line contains n integer numbers xi (0 ≤ xi ≤ 10^9). The last line contains n integer numbers wi (0 < wi < 10^9).
输出
One line for each case, print a single integer number— the weighted median of the sequence.
示例输入
7 10 35 5 10 15 5 20 10 35 5 10 15 5 20
示例输出
20
提示
The S which indicates the sum of all weights may be exceed a 32-bit integer. If S is 5,  equals 2.5.
equals 2.5.
int n;
struct Node
{
int x,w;
}node[maxn];
bool cmp(Node a,Node b)
{
if(a.x<b.x)
return true;
return false;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
long long sum=0;
for(int i=1;i<=n;i++)
scanf("%d",&node[i].x);
for(int i=1;i<=n;i++)
{
scanf("%d",&node[i].w);
sum+=node[i].w;
}
long double S=sum*0.5;
sort(node+1,node+1+n,cmp);
long long xiao=0,da=0;
int ans;
for(int i=1;i<=n-1;i++)
{
xiao+=node[i].w;
da=sum-xiao-node[i+1].w;
if(xiao<S&&da<=S)
{
ans=node[i+1].x;
break;
}
}
cout<<ans<<endl;
}
return 0;
}
http://mycodebattle.github.io/2015/02/SDUT-2886/LL QuickSort(int l, int r, LL small, LL large){int index = l, pivot = arr[l].X;swap(arr[l], arr[r]);for (int i = l; i < r; i++)if (arr[i].X < pivot) swap(arr[index++], arr[i]);swap(arr[index], arr[r]);LL sm = 0, equ = 0, big = 0;for (int i = l; i <= r; i++){if (arr[i].X < pivot) sm += arr[i].Y;else if (arr[i].X == pivot) equ += arr[i].Y;else big += arr[i].Y;}if ((small+sm)*2 < sum && (large+big)*2 <= sum) return pivot;if ((small+sm)*2 >= sum) return QuickSort(l, index-1, small, large+equ+big);while (index < r && arr[index].X == arr[index+1].X) index++;if ((large+big)*2 > sum) return QuickSort(index+1, r, small+equ+sm, large);}int main(){//ROP;int n;while (~scanf("%d", &n)){sum = 0;for (int i = 0; i < n; i++)scanf("%d", &arr[i].X);for (int i = 0; i < n; i++){scanf("%d", &arr[i].Y);sum += arr[i].Y;}printf("%lld\n", QuickSort(0, n-1, 0, 0));}return 0;}
https://en.wikipedia.org/wiki/Weighted_median
Weighted median can be computed by sorting the set of numbers and finding the smallest numbers which sums to half the weight of total weight. This algorithm takes
 time. There is a better approach to find weighted median using a modified selection algorithm
time. There is a better approach to find weighted median using a modified selection algorithmWeightedMedian(a[1..n], p, r)
//base case for single element
if r = p
return a[p]
//base case for two elements
//make sure we return lower median
if r-p = 1
if a[p].w >= a[r].w
return a[p]
else return a[r]
//partition around pivot r
q = partition(a, p, r)
wl, wg = sum weights of partitions (p, q-1), (q+1, r)
//if partitions are balanced then we are done
if wl and wg both < 1/2
return a[q]
else
//increase pivot weight by the amount of partition we eliminate
if wl > wg
a[q].w += wg
//recurse on pivot inclusively
WeightedMedian(a, p, q)
else
a[q].w += wl
WeightedMedian(a, q, r)
As the recursive call in inclusive of median, recurrence relation is,

Which yields  runtime.
runtime.
https://github.com/gzc/CLRS/blob/master/C09-Medians-and-Order-Statistics/problem.md runtime.
runtime.https://github.com/gzc/CLRS/blob/master/C09-Medians-and-Order-Statistics/problems/weighted_median.py
| |||
| smaller = [item for item in items if item < med] | |||
| larger = [item for item in items if item > med] | |||
| if len(smaller) == n: | |||
| return med | |||
| elif len(smaller) > n: | |||
| return select(smaller, n) | |||
| else: | |||
| return select(list(larger), n - len(smaller) - 1) | |||
| def median(items): | |||
| def median_index(n): | |||
| if n % 2: | |||
| return n // 2 | |||
| else: | |||
| return n // 2 - 1 | |||
| def partition(items, element): | |||
| i = 0 | |||
| for j in range(len(items) - 1): | |||
| if items[j] == element: | |||
| items[j], items[-1] = items[-1], items[j] | |||
| if items[j] < element: | |||
| items[i], items[j] = items[j], items[i] | |||
| i += 1 | |||
| items[i], items[-1] = items[-1], items[i] | |||
| return i | |||
| def select(items, n): | |||
| if len(items) <= 1: | |||
| return items[0] | |||
| medians = [] | |||
| for i in range(0, len(items), 5): | |||
| group = sorted(items[i:i + 5]) | |||
| items[i:i + 5] = group | |||
| median = group[median_index(len(group))] | |||
| medians.append(median) | |||
| pivot = select(medians, median_index(len(medians))) | |||
| index = partition(items, pivot) | |||
| if n == index: | |||
| return items[index] | |||
| elif n < index: | |||
| return select(items[:index], n) | |||
| else: | |||
| return select(items[index + 1:], n - index - 1) | |||
| return select(items[:], median_index(len(items))) | |||
| def weighted_median(items, w_items, start, end): | |||
| def linear_weighted_median(items, start, end): | |||
| med = median(items) | |||
| smaller = [item for item in items if item < med] | |||
| larger = [item for item in items if item > med] | |||
| leftsum = 0 | |||
| rightsum = 0 | |||
| for i in range(len(smaller)): | |||
| leftsum += m[smaller[i]] | |||
| for i in range(len(smaller)): | |||
| rightsum += m[larger[i]] | |||
| print leftsum,rightsum | |||
| if leftsum < 0.5 and rightsum <= 0.5: | |||
| return med | |||
| if leftsum >= 0.5: | |||
| m[med] += rightsum | |||
| smaller.append(med) | |||
| return linear_weighted_median(smaller, start, start+len(smaller)-1) | |||
| else: | |||
| m[med] += leftsum | |||
| larger.insert(0, med) | |||
| return linear_weighted_median(larger, start+len(smaller)+1, end) | |||
| m = dict() | |||
| for i in range(len(items)): | |||
| m[items[i]] = w_items[i] | |||
| return linear_weighted_median(items, start, end) | |||
| weighted_array = [0.3,0.3,0.1,0.05,0.25] | |||
| array = [5,4,0,3,2] | |||
| print weighted_median(array, weighted_array, 0, 4) |