Massive Algorithms: [CC150v5] 9.11 Parenthesize the Expression

[CC150v5] 9.11 Parenthesize the Expression - Shuatiblog.com

[CC150v5] 9.11 Parenthesize the Expression - Shuatiblog.com
Given a boolean expression consisting of the symbols 0, 1, '&', '|', and '^', and a desired boolean result value 'result'.
Now implement a function to count the number of ways of parenthesizing the expression such that it evaluates to 'result'.

https://algorithmsandme.com/boolean-parenthesization-problem/

Complexity of dynamic programming approach to find ways to parenthesize a Boolean expression to evaluate it to True is O(n3). and space complexity is O(n2) .

    public static int calculateNumberOfWays(String operators, String operands){

        int numOperands = operands.length();

        int[][] F = new int[numOperands][numOperands];

        int[][] T = new int [numOperands][numOperands];

        for (int i=0; i<numOperands; i++){

            System.out.println(operands.charAt(i));

            F[i][i] = (operands.charAt(i) == 'F')? 1: 0;

            T[i][i] = (operands.charAt(i) == 'T')? 1: 0;

            System.out.println(T[i][i]);

}

        for (int L=1; L<numOperands; L++) {

            for (int i=0; i<numOperands-L; ++i){

                int j = i+L;

                T[i][j] = F[i][j] = 0;

                for (int k=i; k<j; k++){

                    int totalIK = T[i][k] + F[i][k];

                    int totalKJ = T[k+1][j] + F[k+1][j];

                    if (operators.charAt(k) == '&') {

                        T[i][j] += T[i][k]*T[k+1][j];

                        F[i][j] += (totalIK *totalKJ - T[i][k]*T[k+1][j]);

}

                    if (operators.charAt(k) == '|'){

                        F[i][j] += F[i][k]*F[k+1][j];

                        T[i][j] += (totalIK*totalKJ - F[i][k]*F[k+1][j]);

}

                    if (operators.charAt(k) == '^'){

                        T[i][j] += F[i][k]*T[k+1][j] + T[i][k]*F[k+1][j];

                        F[i][j] += T[i][k]*T[k+1][j] + F[i][k]*F[k+1][j];

}

}

}

}

        for(int i=0; i<numOperands; i++){

            for(int j=0; j<numOperands; j++){

                System.out.println("(" + i + "," + j + ") :"  + T[i][j]);

}

}

        return T[0][numOperands-1];

}

Each parenthesized expression must have an outermost pair of parentheses.
That is, we can iterate through the expression, treating each operator as the first operator to be parenthesized.

So for each operator, we consider is as first operator (to evaluate), and then we shall if the total possible count.

public static int countMyAnswer(String exp, boolean result) {
    if (exp.length() == 1) {
        return convertIntToBool(exp.charAt(0)) == result ? 1 : 0;
    }
    // eg. 1^0|0|1
    // result: true
    int totalCount = 0;
    for (int i = 1; i < exp.length(); i += 2) {

        char op = exp.charAt(i);
        String firstHalf = exp.substring(0, i);
        String secondHalf = exp.substring(i + 1);

        int firstHalfTrue = countMyAnswer(firstHalf, true);
        int firstHalfFalse = countMyAnswer(firstHalf, false);
        int secondHalfTrue = countMyAnswer(secondHalf, true);
        int secondHalfFalse = countMyAnswer(secondHalf, false);

        if (evaluate('0', op, '0') == result) {
            totalCount += firstHalfFalse * secondHalfFalse;
        }
        if (evaluate('0', op, '1') == result) {
            totalCount += firstHalfFalse * secondHalfTrue;
        }
        if (evaluate('1', op, '0') == result) {
            totalCount += firstHalfTrue * secondHalfFalse;
        }
        if (evaluate('1', op, '1') == result) {
            totalCount += firstHalfTrue * secondHalfTrue;
        }
    }
    return totalCount;
}

private static boolean convertIntToBool(char num) {
    if (num == '1') {
        return true;
    } else {
        return false;
    }
}

private static boolean evaluate(char num1, char op, char num2) {
    boolean b1 = convertIntToBool(num1);
    boolean b2 = convertIntToBool(num2);
    if (op == '&') {
        return b1 & b2;
    } else if (op == '|') {
        return b1 | b2;
    } else if (op == '^') {
        return b1 ^ b2;
    }
    System.out.println("Did not found operator " + op);
    return false;
}

https://miafish.wordpress.com/2015/01/03/boolean-parenthesization-problem/
Recursion Solution: we can see this problem as function(expression, result). we go through all the operators in the expression, so the function(expression, result) split into two functions function(expression left, result); function(expression right, result). continue to split it until the length of expression is 1.

        public int GetWaysOfParenthesizeExpressionRecursion(string expression, bool result)
        {
            if (expression.Count() == 1)
            {
                return (expression.Equals("1") && result) || (expression.Equals("0") && !result) ? 1 : 0;
            }

            var count = 0;
            for (var i = 1; i < expression.Count() - 1; i = i + 2)
            {
                var left = expression.Substring(0, i);
                var right = expression.Substring(i + 1);
                switch (expression[i])
                {
                    case '|':
                        {
                            if (result)
                            {
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, true)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, true);
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, true)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, false);
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, false)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, true);
                            }
                            else
                            {
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, false)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, false);
                            }
                        }
                        break;
                    case '&':
                        {
                            if (result)
                            {
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, true)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, true);
                            }
                            else
                            {
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, true)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, false);
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, false)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, true);
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, false)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, false);
                            }
                        }
                        break;
                    case '^':
                        {
                            if (result)
                            {
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, true)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, false);
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, false)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, true);
                            }
                            else
                            {
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, true)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, true);
                                count += this.GetWaysOfParenthesizeExpressionRecursion(left, false)
                                         * this.GetWaysOfParenthesizeExpressionRecursion(right, false);
                            }
                        }
                        break;
                }
            }

            return count;
        }

Dynamic programming Solution: as we found in the recursion solution, there are lots of expressions that we have calculated multiple times. we can use 3 dimensions array to store all the values. DP[expression length][expression length][2 – True or False]

DP[start][end][True or False] – Expression starts at start point, end at end points and desired result is true or false, how many ways we can parenthesize the expression.

so for all DP[start][start][] will depend on it is 1 or 0, if it is 1, DP[start][start][1] = 1; otherwise DP[start][start][0] = 1;

then we use loop to find DP[start][start + 2.4.6…][0 or 1].

For example: 1^0|0|1

initial it would DP[0][0][1] = 1; DP[2][2][0] = 1; DP[4][4][0] = 1; DP[6][6][1] = 1;

then we start to gap 2 values

DP[0][2][0 or 1]; DP[2][4][0 or 1]; DP[4][6][0 or 1] from all the previous values we know

then gap 4 values

DP[0][4][0 or 1]; DP[2][6][0 or 1];

then gap 6 values

DP[0][6][0 or 1] which is what we want.

        public int GetWaysOfParenthesizeExpressionDP(string expression, bool result)
        {
            // dp[start][end][result - False or True]
            var size = expression.Count();
            var dp = new int[size][][];
            for (var i = 0; i < size; i++)
            {
                dp[i] = new int[size][];
                for (var j = 0; j < size; j++)
                {
                    // 0  for false; 1 for true
                    dp[i][j] = new int[2];
                }
            }

            for (var i = 0; i < size; i = i + 2)
            {
                if (expression[i].Equals('1'))
                {
                    dp[i][i][1] = 1;
                }
                else
                {
                    dp[i][i][0] = 1;
                }
            }


            for (var length = 3; length <= size; length = length + 2)
            {
                for (var start = 0; start + length <= size; start = start + 2)
                {
                    for (var k = start + 1; k < start + length; k = k + 2)
                    {
                        var end = start + length - 1;
                        switch (expression[k])
                        {
                            case '|':
                            {
                                dp[start][end][1] += dp[start][k - 1][1] * dp[k + 1][end][1]
                                                          + dp[start][k - 1][0] * dp[k + 1][end][1]
                                                          + dp[start][k - 1][1] * dp[k + 1][end][0];
                                dp[start][end][0] += dp[start][k - 1][0] * dp[k + 1][end][0];
                            }
                                break;
                            case '&':
                            {
                                dp[start][end][1] += dp[start][k - 1][1] * dp[k + 1][end][1];
                                dp[start][end][0] += dp[start][k - 1][0] * dp[k + 1][end][1]
                                                          + dp[start][k - 1][1] * dp[k + 1][end][0]
                                                          + dp[start][k - 1][0] * dp[k + 1][end][0];
                            }
                                break;
                            case '^':
                            {
                                dp[start][end][1] += dp[start][k - 1][1] * dp[k + 1][end][0]
                                                          + dp[start][k - 1][0] * dp[k + 1][end][1];
                                dp[start][end][0] += dp[start][k - 1][1] * dp[k + 1][end][1]
                                                          + dp[start][k - 1][0] * dp[k + 1][end][0];
                            }
                                break;
                        }
                    }
                }
            }


            return dp[0][size - 1][result ? 1 : 0];
        }

With Cache:
int countEval(String s, boolean result, HashMap<String, Integer> memo) {
if (s.length() 0) return 0;
if (s.length() == 1) return stringToBool(s) ==result ? 1 : 0;
if (memo.containsKey(result + s)) return memo.get(result + s);
int ways = 0;
for (int i= 1; 1 < s.length(); i += 2) {
char c = s.charAt(i);
String left = s.substring(0, i);
String right = s.substring(i + 1, s.length());
int leftTrue = countEval(left, true, memo);
int leftFalse = countEval(left, false, memo);
int rightTrue = countEval(right, true, memo);
int rightFalse = countEval(right, false, memo);
int total= (leftTrue + leftFalse) * (rightTrue + rightFalse);
int totalTrue = 0;
if ( C == "^") {
totalTrue = leftTrue * rightFalse + leftFalse * rightTrue;
} else if (c == '&') {
totalTrue = leftTrue * rightTrue;
} el se if (c == '|') {
}
totalTrue = leftTrue * right True + leftFalse * rightTrue +
leftTrue * rightFalse;
int subways = result ? totalTrue total - totalTrue;
ways += subways;
}
memo.put(result + s, ways);
return ways;
}

int countEval(String s, boolean result) {
if (s.length() == 0) return 0;
if (s.length() == 1) return stringToBool(s);

int ways= 0;
for (int i= 1; i < s.length(); i += 2) {
char c = s.charAt(i);
String left= s.substring(0, i);
String right= s.substring(i + 1, s.length());

/* Evaluate each side for each result. */
int leftTrue = countEval(left, true);
int leftFalse countEval(left, false);
int rightTrue = countEval(right, true);
int rightFalse = countEval(right, false);
int total= (leftTrue + leftFalse) * (rightTrue + rightFalse);

int totalTrue = 0;
if (c == '^') { // required : one true and one false
totalTrue = leftTrue * rightFalse + leftFalse * rightTrue;
} else if (c == '&') {
//required: both true
totalTrue = leftTrue * rightTrue;
} else if (c == '|') { // required: anything but both false
totalTrue = leftTrue * rightTrue + leftFalse * rightTrue +
leftTrue * rightFalse;
}

int subways= result ? totalTrue:total - totalTrue;
ways+= subways;
}

return ways;
}

boolean stringToBool(String c) {
return c.equals("l") ? true : false;
}

Our current code is blind to what we do and don't actually need to do and instead just computes all of

the values. This is probably a reasonable tradeoff to make (especially given the constraints of whiteboard coding) as it makes our code substantially shorter and less tedious to write. Whichever approach you make, you should discuss the tradeoffs with your interviewer.

There is one further optimization we can make, but it's far beyond the scope of the interview. There is a closed form expression for the number of ways of parenthesizing an expression,.

It is given by the Catalan numbers, where n is the number of operators:

C (2n),

n - (n+l) !n! We could use this to compute the total ways of evaluating the expression. Then, rather than computing leftTrue and leftFalse, we just compute one of those and calculate the other using the Catalan

numbers. We would do the same thing for the right side.

TODO: http://blog.csdn.net/fightforyourdream/article/details/16983025

http://codinginterview.net/post/given-a-boolean-expression-and-a-desired-result-value-implement-a-function-to-count-the-number-of-ways-of-parenthesizing-the-expression-such-that-it-evaluates-to-this-value

https://github.com/gaylemcd/ctci/blob/master/python/Chapter%209/Question9_11/parenthesizing.py

https://www.geeksforgeeks.org/boolean-parenthesization-problem-dp-37/

Let the input be in form of two arrays one contains the symbols (T and F) in order and other contains operators (&, | and ^}

Examples:

Input: symbol[]    = {T, F, T}
       operator[]  = {^, &}
Output: 2
The given expression is "T ^ F & T", it evaluates true
in two ways "((T ^ F) & T)" and "(T ^ (F & T))"

Let T(i, j) represents the number of ways to parenthesize the symbols between i and j (both inclusive) such that the subexpression between i and j evaluates to true.
$T(i,j)=\sum_{k=i}^{j-1}\begin{Bmatrix} T(i,k)*T(k+1,j) & if&operator&[k]is '\&'\\ Total(i,k)*Total(k+1,j)-F(i,k)*F(k+1,j) &if&operator&[k]&is'|' \\ T(i,k)*F(k+1,j)+F(i,k)*T(k+1,j) &if&operator&[k]&is '\oplus' \end{Bmatrix} Total(i,j)= T(i,j)+F(i,j)$
<!–

–>

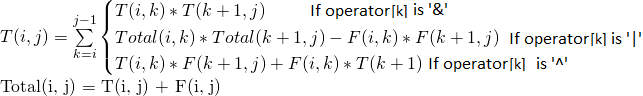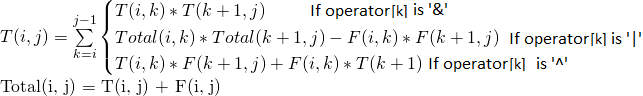Let F(i, j) represents the number of ways to parenthesize the symbols between i and j (both inclusive) such that the subexpression between i and j evaluates to false.

$F(i,j)=\sum_{k=i}^{j-1} \begin{Bmatrix} Total(i,k)*Total(k+1,j)-T(i,k)*T(k+1,j) & if&operator[k]&is'\&'\\ F(i,k)*F(k+1,j) &if&operator[k] &is'|' \\ T(i,k)*T(k+1,j)+F(i,k)*F(k+1,j) &if&operator[k]&is'\oplus' \end{Bmatrix} Total(i,j)=T(i,j)+F(i,j)$
<!—

–>
Base Cases:

T(i, i) = 1 if symbol[i] = 'T' 
T(i, i) = 0 if symbol[i] = 'F' 

F(i, i) = 1 if symbol[i] = 'F' 
F(i, i) = 0 if symbol[i] = 'T'

int countParenth(char symb[], char oper[], int n) 

{ 

    int F[n][n], T[n][n]; 

    // Fill diaginal entries first 

    // All diagonal entries in T[i][i] are 1 if symbol[i] 

    // is T (true).  Similarly, all F[i][i] entries are 1 if 

    // symbol[i] is F (False) 

    for (int i = 0; i < n; i++) 

    { 

        F[i][i] = (symb[i] == 'F')? 1: 0; 

        T[i][i] = (symb[i] == 'T')? 1: 0; 

    } 

    // Now fill T[i][i+1], T[i][i+2], T[i][i+3]... in order 

    // And F[i][i+1], F[i][i+2], F[i][i+3]... in order 

    for (int gap=1; gap<n; ++gap) 

    { 

        for (int i=0, j=gap; j<n; ++i, ++j) 

        { 

            T[i][j] = F[i][j] = 0; 

            for (int g=0; g<gap; g++) 

            { 

                // Find place of parenthesization using current value 

                // of gap 

                int k = i + g; 

                // Store Total[i][k] and Total[k+1][j] 

                int tik = T[i][k] + F[i][k]; 

                int tkj = T[k+1][j] + F[k+1][j]; 

                // Follow the recursive formulas according to the current 

                // operator 

                if (oper[k] == '&') 

                { 

                    T[i][j] += T[i][k]*T[k+1][j]; 

                    F[i][j] += (tik*tkj - T[i][k]*T[k+1][j]); 

                } 

                if (oper[k] == '|') 

                { 

                    F[i][j] += F[i][k]*F[k+1][j]; 

                    T[i][j] += (tik*tkj - F[i][k]*F[k+1][j]); 

                } 

                if (oper[k] == '^') 

                { 

                    T[i][j] += F[i][k]*T[k+1][j] + T[i][k]*F[k+1][j]; 

                    F[i][j] += T[i][k]*T[k+1][j] + F[i][k]*F[k+1][j]; 

                } 

            } 

        } 

    } 

    return T[0][n-1]; 

}

X. https://www.johndcook.com/blog/2013/10/03/parenthesize-expression-catalan/

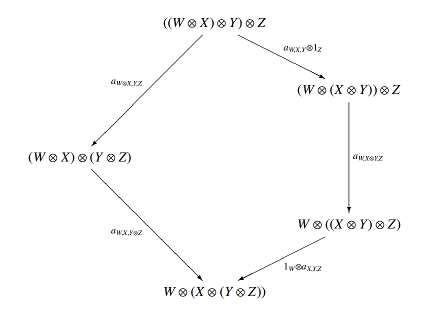
Here’s a pentagonal diagram from a paper by John Baez and Mike Stay. Why is it a pentagon?

There are five ways to parenthesize an expression with four terms, and the diagram is showing how all ways of parenthesizing four terms are related.

How do we know that there are five ways to parenthesize four terms? We could list them, but then how do we know we didn’t leave out a possibility?

It turns out that the number of ways to parenthesize an expression with n+1 terms is Cn, the nth Catalan number. An expression for the Catalan numbers can be derived by starting with a recurrence relation that the numbers must satisfy and then producing their generating function. The end result is the following identity:

$C_n = \frac{1}{n+1}{2n\choose n}$
If we set n = 3, we get C3 = 5, confirming that there are five ways to parenthesize four terms.

The Catalan number pop up in many applications. For example, Richard Stanley has posted a 96-page PDF file of combinatorial problems whose solution involves Catalan numbers.

Here’s an odd observation regarding Catalan numbers. If Cn is an odd Catalan number, then n = 2k – 1. And it appears that if k ≥ 9, the last digit of Cn is always 5, though this has not been proven.

[CC150v5] 9.11 Parenthesize the Expression - Shuatiblog.com

Labels

Popular Posts