Related: Box Stacking Problem
https://leetcode.com/problems/remove-boxes
http://www.lydxlx.net/2017/03/26/first-post/
http://www.cnblogs.com/grandyang/p/6850657.html
在之前帖子Reverse Pairs的讲解中,大神归纳了两种重现模式,我们这里也试着看能不能套用上。对于这种看来看去都没思路的题来说,抽象建模的能力就非常的重要了。对于题目中的具体场景啊,具体代表的东西我们都可忽略不看,这样能帮助我们接近问题的本质,这道题的本质就是一个数组,我们每次消去一个或多个数字,并获得相应的分数,让我们求最高能获得的分数。而之前那道Zuma Game也是给了一个数组,让我们往某个位置加数字,使得相同的数字至少有3个才能消除,二者是不是很像呢,但是其实解法却差别很大。那道题之所以暴力破解没有问题是因为数组的长度和给定的数字个数都有限制,而且都是相对较小的数,那么即便遍历所有情况也不会有太大的计算量。而这道题就不一样了,既然不能暴力破解,那么对于这种玩数组和子数组的题,刷题老司机们都会优先考虑用DP来做吧。既然要玩子数组,肯定要限定子数组的范围,那么至少应该是个二维的dp数组,其中dp[i][j]表示在子数组[i, j]范围内所能得到的最高的分数,那么最后我们返回dp[0][n-1]就是要求的结果。
那么对于这道题来说,无法处理boxes[m, j]区间是因为其缺少了关键信息,我们不知道boxes[m]左边相同数字的个数k,只有知道了这个信息,那么m的位置才有意义,所以我们的dp数组应该是一个三维数组dp[i][j][k],表示区间[i, j]中能获得的最大积分,当boxes[i]左边有k个数字跟其相等,那么我们的目标就是要求dp[0][n-1][0]了,而且我们也能推出dp[i][i][k] = (1+k) * (1+k)这个等式。那么我们来推导重现关系,对于dp[i][j][k],如果我们移除boxes[i],那么我们得到(1+k)*(1+k) + dp[i+1][j][0]。对于上面提到的那种情况,当某个位置m,有boxes[i] == boxes[m]时,我们也应该考虑先移除[i+1,m-1]这部分,我们得到积分dp[i+1][m-1][0],然后再处理剩下的部分,得到积分dp[m][j][k+1],这里k加1点原因是,移除了中间的部分后,原本和boxes[m]不相邻的boxes[i]现在相邻了,又因为二者值相同,所以k应该加1,因为k的定义就是左边相等的数字的个数。讲到这里,那么DP方法最难的递推公式也就得到了,那么代码就不难写了,需要注意的是,这里的C++的写法不能用vector来表示三维数组,好像是内存限制超出,只能用C语言的写法,由于C语言数组的定义需要初始化大小,而题目中说了数组长度不会超100,所以我们就用100来初始化
https://leetcode.com/problems/remove-boxes/discuss/101325/java-dp-memorization-60ms
http://www.codingblog.cn/blog/34458.html
http://blog.csdn.net/yy254117440/article/details/67638980
http://www.codingblog.cn/blog/34458.html
https://mikecoder.github.io/oj-code/2017/05/06/RemoveBoxes/
http://www.cnblogs.com/heisenberg-/p/6789708.html
http://blog.csdn.net/raorang/article/details/72584957
https://leetcode.com/problems/remove-boxes/discuss/101310/Java-top-down-and-bottom-up-DP-solutions
X.
下面这种写法是上面解法的迭代方式,但是却有一些不同,这里我们需要对dp数组的部分值做一些初始化,将每个数字的所有k值的情况的积分都先算出来,然后在整体更新三维dp数组的时候也很有意思,并不是按照原有的顺序更新,而是块更新,先更新dp[1][0][k], dp[2][1][k], dp[3][2][k]....,再更新dp[2][0][k], dp[3][1][k], dp[4][2][k]...., 再更新dp[3][0][k], dp[4][1][k], dp[5][2][k]....,之前好像也有一道是这样区域更新的题
https://leetcode.com/problems/remove-boxes
Given several boxes with different colors represented by different positive numbers.
You may experience several rounds to remove boxes until there is no box left. Each time you can choose some continuous boxes with the same color (composed of k boxes, k >= 1), remove them and get
Find the maximum points you can get.
You may experience several rounds to remove boxes until there is no box left. Each time you can choose some continuous boxes with the same color (composed of k boxes, k >= 1), remove them and get
k*k points.Find the maximum points you can get.
Example 1:
Input:
Input:
[1, 3, 2, 2, 2, 3, 4, 3, 1]Output:
23Explanation:
[1, 3, 2, 2, 2, 3, 4, 3, 1] ----> [1, 3, 3, 4, 3, 1] (3*3=9 points) ----> [1, 3, 3, 3, 1] (1*1=1 points) ----> [1, 1] (3*3=9 points) ----> [] (2*2=4 points)
Note: The number of boxes
X.n would not exceed 100.
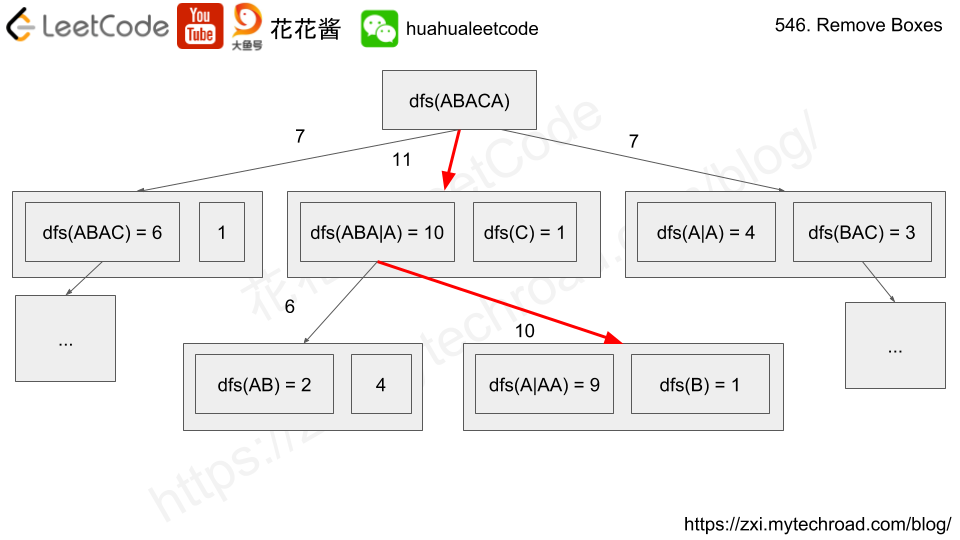
Use dp[l][r][k] to denote the max score of subarray box[l] ~ box[r] with k boxes after box[r] that have the same color as box[r]
box[l], box[l+1], …, box[r], box[r+1], …, box[r+k]
e.g. “CDABACAAAAA”
dp[2][6][4] is the max score of [ABACA] followed by [AAAA]
dp[2][6][3] is the max score of [ABACA] followed by [AAA]
dp[2][6][3] is the max score of [ABACA] followed by [AAA]
base case: l > r, empty array, return 0.
Transition:
dp[l][r][k] = max(dp[l][r-1][0] + (k + 1)*(k + 1), # case 1
dp[l][i][k+1] + dp[i+1][r-1][0]) # case 2
# "ABACA|AAAA"
# case 1: dp("ABAC") + score("AAAAA") drop j and the tail.
# case 2: box[i] == box[r], l <= i < r, try all break points
# max({dp("A|AAAAA") + dp("BAC")}, {dp("ABA|AAAAA") + dp("C")})
Time complexity: O(n^4)
Space complexity: O(n^3)
int removeBoxes(vector<int>& boxes) {
const int n = boxes.size();
m_ = vector<vector<vector<int>>>(n, vector<vector<int>>(n, vector<int>(n)));
return dfs(boxes, 0, n - 1, 0);
}
private:
vector<vector<vector<int>>> m_;
int dfs(const vector<int>& boxes, int l, int r, int k) {
if (l > r) return 0;
if (m_[l][r][k] > 0) return m_[l][r][k];
m_[l][r][k] = dfs(boxes, l, r - 1, 0) + (k + 1) * (k + 1);
for (int i = l; i < r; ++i)
if (boxes[i] == boxes[r])
m_[l][r][k] = max(m_[l][r][k], dfs(boxes, l, i, k + 1) + dfs(boxes, i + 1, r - 1, 0));
return m_[l][r][k];
}
int m[100][100][100];
class Solution {
int removeBoxes(vector<int>& boxes) {
memset(m, 0, sizeof(m));
return dfs(boxes, 0, boxes.size() - 1, 0);
}
int dfs(const vector<int>& boxes, int l, int r, int k) {
if (l > r) return 0;
if (m[l][r][k] > 0) return m[l][r][k];
int rr = r;
int kk = k;
while (l < r && boxes[r - 1] == boxes[r]) {--r; ++k;}
m[l][r][k] = dfs(boxes, l, r - 1, 0) + (k + 1) * (k + 1);
for (int i = l; i < r; ++i)
if (boxes[i] == boxes[r])
m[l][r][k] = max(m[l][r][k], dfs(boxes, l, i, k + 1) + dfs(boxes, i + 1, r - 1, 0));
for (int d = 1; d <= r - rr; ++d)
m[l][r + d][k - d] = m[l][r][k];
return m[l][r][k];
}
Use a HashTable to replace the 3D DP array since the DP array could be sparse when many consecutive boxes are the same color.
int removeBoxes(vector<int>& boxes) {
len_ = vector<int>(boxes.size());
for (int i = 1; i < boxes.size(); ++i)
if (boxes[i] == boxes[i - 1]) len_[i] = len_[i - 1] + 1;
return dfs(boxes, 0, boxes.size() - 1, 0);
}
private:
unordered_map<int, int> m_;
vector<int> len_;
int dfs(const vector<int>& boxes, int l, int r, int k) {
if (l > r) return 0;
k += len_[r];
r -= len_[r];
int key = (l * 100 + r) * 100 + k;
auto it = m_.find(key);
if (it != m_.end()) return it->second;
int& ans = m_[key];
ans = dfs(boxes, l, r - 1, 0) + (k + 1) * (k + 1);
for (int i = l; i < r; ++i)
if (boxes[i] == boxes[r])
ans = max(ans, dfs(boxes, l, i, k + 1) + dfs(boxes, i + 1, r - 1, 0));
return ans;
}
The above DP solution seems to run in time as there are states for and each state roughly takes time in average to transit. However, the bound is not tight, and the tight one is , which can be shown via a more careful analysis.
We cluster into several clusters based on the the value of . Say there are in total clusters, and the -cluster contains indices of . We then have . When we fix a cluster, there can be at most different states involved. Since different clusters are disjoint, the total number of meaningful states is also bounded by .
http://www.cnblogs.com/grandyang/p/6850657.html
在之前帖子Reverse Pairs的讲解中,大神归纳了两种重现模式,我们这里也试着看能不能套用上。对于这种看来看去都没思路的题来说,抽象建模的能力就非常的重要了。对于题目中的具体场景啊,具体代表的东西我们都可忽略不看,这样能帮助我们接近问题的本质,这道题的本质就是一个数组,我们每次消去一个或多个数字,并获得相应的分数,让我们求最高能获得的分数。而之前那道Zuma Game也是给了一个数组,让我们往某个位置加数字,使得相同的数字至少有3个才能消除,二者是不是很像呢,但是其实解法却差别很大。那道题之所以暴力破解没有问题是因为数组的长度和给定的数字个数都有限制,而且都是相对较小的数,那么即便遍历所有情况也不会有太大的计算量。而这道题就不一样了,既然不能暴力破解,那么对于这种玩数组和子数组的题,刷题老司机们都会优先考虑用DP来做吧。既然要玩子数组,肯定要限定子数组的范围,那么至少应该是个二维的dp数组,其中dp[i][j]表示在子数组[i, j]范围内所能得到的最高的分数,那么最后我们返回dp[0][n-1]就是要求的结果。
那么对于dp[i][j]我们想,如果我们移除boxes[i]这个数字,那么总得分应该是1 + dp[i+1][j],但是通过分析题目中的例子,能够获得高积分的trick是,移除某个或某几个数字后,如果能使得原本不连续的相同数字变的连续是坠好的,因为同时移除的数字越多,那么所得的积分就越高。那么假如在[i, j]中间有个位置m,使得boxes[i]和boxes[m]相等,那么我们就不应该只是移除boxes[i]这个数字,而是还应该考虑直接移除[i+1, m-1]区间上的数,使得boxes[i]和boxes[m]直接相邻,那么我们获得的积分就是dp[i+1][m-1],那么我们剩余了什么,boxes[i]和boxes[m, j]区间的数,此时我们无法处理子数组[m, j],因为我们有些信息没有包括在我们的dp数组中,此类的题目归纳为不自己包含的子问题,其解法依赖于一些子问题以外的信息。这类问题通常没有定义好的重现关系,所以不太容易递归求解。为了解决这类问题,我们需要修改问题的定义,使得其包含一些外部信息,从而变成自包含子问题。
int removeBoxes(vector<int>& boxes) { int n = boxes.size(); int dp[100][100][100] = {0}; return helper(boxes, 0, n - 1, 0, dp); } int helper(vector<int>& boxes, int i, int j, int k, int dp[100][100][100]) { if (j < i) return 0; if (dp[i][j][k] > 0) return dp[i][j][k]; int res = (1 + k) * (1 + k) + helper(boxes, i + 1, j, 0, dp); for (int m = i + 1; m <= j; ++m) { if (boxes[m] == boxes[i]) { res = max(res, helper(boxes, i + 1, m - 1, 0, dp) + helper(boxes, m, j, k + 1, dp)); } } return dp[i][j][k] = res; }X. DP 2
https://leetcode.com/problems/remove-boxes/discuss/101325/java-dp-memorization-60ms
When facing this problem, I am keeping thinking how to simulate the case when
boxes[i] == boxes[j] when i and j are not consecutive. It turns out that the dp matrix needs one more dimension to store such state. So we are going to define the state asdp[i][j][k] represents the max points from box[i] to box[j] with k boxes whose values equal to box[i]
The transformation function is as below
dp[i][j][k] = max(dp[i+1][m-1][1] + dp[m][j][k+1]) when box[i] = box[m]
From your explanation
dp[i][j][k] represents the max points from box[i] to box[j] with k boxes whose values equal to box[i]
However, I think dp[i][j][k] should mean the max points from box[i] to box[j] with k boxes of value box[i] merged.
And also the DP
We have two condition
- We choose to merge k boxes
this mean we would have score = dp(i+1, j, 1) + k * k ...............(1)
- We don't merge k boxes
so, we can continue to find box which is the same
this means when we find box m equal to box i, we can have one more box, so k become k + 1
So we have dp(i+1, m-1, 1) + dp (m, j, k + 1) ...............(2)
the first term is the other boxes
and the second term contain information of the same boxes(box[i] or box[m]) we have found till now
dp[i][j][k] = max ((1), (2))
public int removeBoxes(int[] boxes) {
if (boxes == null || boxes.length == 0) {
return 0;
}
int size = boxes.length;
int[][][] dp = new int[size][size][size];
return get(dp, boxes, 0, size-1, 1);
}
private int get(int[][][] dp, int[] boxes, int i, int j, int k) {
if (i > j) {
return 0;
} else if (i == j) {
return k * k;
} else if (dp[i][j][k] != 0) {
return dp[i][j][k];
} else {
int temp = get(dp, boxes, i + 1, j, 1) + k * k;
for (int m = i + 1; m <= j; m++) {
if (boxes[i] == boxes[m]) {
temp = Math.max(temp, get(dp, boxes, i + 1, m - 1, 1) + get(dp, boxes, m, j, k + 1));
}
}
dp[i][j][k] = temp;
return temp;
}
}http://www.codingblog.cn/blog/34458.html
http://blog.csdn.net/yy254117440/article/details/67638980
整体思路类似于分治和记忆化存储
三维dp,直接看下面这种情况:
三维dp,直接看下面这种情况:
- 1
- 1
用dp[i][j][k] 存储可获得的最大分数,其中i是左边界,j是又边界,k是和右边界相等的后缀长度。上面例子如下:
- 1
- 2
- 1
- 2
对于当前左右边界和相应的k值,可以对右边界后k个元素进行merge操作得分:
- 1
- 1
也可以不merge,从左往右如果找到一个值和box[r]相等则将原数组分为两部分求值:
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
http://www.codingblog.cn/blog/34458.html
https://mikecoder.github.io/oj-code/2017/05/06/RemoveBoxes/
Think about using a DP[100][100][100] to store the status that from [left] to [right] we have [k] same numbers in the end.
So, we can find the status transition way:
|
http://blog.csdn.net/raorang/article/details/72584957
memo[l][r][k] = max(memo[l][r][k], dfs(boxes,memo,l,i,k+1) + dfs(boxes,memo,i+1,r-1,0));
意思是在序列的l-r部分后接k长度的 r值序列 所能得到的最大得分。
X.https://leetcode.com/problems/remove-boxes/discuss/101310/Java-top-down-and-bottom-up-DP-solutions
Since the input is an array, let's begin with the usual approach by breaking it down with the original problem applied to each of the subarrays.
Let the input array be
boxes with length n. Define T(i, j) as the maximum points one can get by removing boxes of the subarray boxes[i, j] (both inclusive). The original problem is identified as T(0, n - 1) and the termination condition is as follows:T(i, i - 1) = 0: no boxes so no points.T(i, i) = 1: only one box left so the maximum point is1.
Next let's try to work out the recurrence relation for
T(i, j). Take the first box boxes[i](i.e., the box at index i) as an example. What are the possible ways of removing it? (Note: we can also look at the last box and the analyses turn out to be the same.)
If it happens to have a color that you dislike, you'll probably say "I don't like this box so let's get rid of it now". In this case, you will first get
1 point for removing this poor box. But still you want maximum points for the remaining boxes, which by definition is T(i + 1, j). In total your points will be 1 + T(i + 1, j).
But later after reading the rules more carefully, you realize that you might get more points if this box (
boxes[i]) can be removed together with other boxes of the same color. For example, if there are two such boxes, you get 4 points by removing them simultaneously, instead of 2 by removing them one by one. So you decide to let it stick around a little bit longer until another box of the same color (whose index is m) becomes its neighbor. Note up to this moment all boxes from index i + 1 to index m - 1 would have been removed. So if we again aim for maximum points, the points gathered so far will be T(i + 1, m - 1). What about the remaining boxes?
At this moment, the boxes we left behind consist of two parts: the one at index
i (boxes[i]) and those of the subarray boxes[m, j], with the former bordering the latter from the left. Apparently there is no way applying the definition of the subproblem to the subarray boxes[m, j], since we have some extra piece of information that is not included in the definition. In this case, I shall call that the definition of the subproblem is not self-contained and its solution relies on information external to the subproblem itself.
Another example of problem that does not have self-contained subproblems is leetcode 312. Burst Balloons, where the maximum coins of subarray
nums[i, j] depend on the two numbers adjacent to nums[i] on the left and to nums[j] on the right. So you may find some similarities between these two problems.
Problems without self-contained subproblems usually don't have well-defined recurrence relations, which renders it impossible to be solved recursively. The cure to this issue can sound simple and straightforward: modify the definition of the problem to absorb the external information so that the new one is self-contained.
So let's see how we can redefine
T(i, j) to make it self-contained. First let's identify the external information. On the one hand, from the point of view of the subarray boxes[m, j], it knows nothing about the number (denoted by k) of boxes of the same color as boxes[m]to its left. On the other hand, given this number k, the maximum points can be obtained from removing all these boxes is fixed. Therefore the external information to T(i, j) is this k. Next let's absorb this extra piece of information into the definition of T(i, j) and redefine it as T(i, j, k) which denotes the maximum points possible by removing the boxes of subarray boxes[i, j] with k boxes attached to its left of the same color as boxes[i]. Lastly let's reexamine some of the statements above:- Our original problem now becomes
T(0, n - 1, 0), since there is no boxes attached to the left of the input array at the beginning. - The termination conditions now will be:
a.T(i, i - 1, k) = 0: no boxes so no points, and this is true for anyk(you can interpret it as nowhere to attach the boxes).
b.T(i, i, k) = (k + 1) * (k + 1): only one box left in the subarray but we've already gotkboxes of the same color attached to its left, so the total number of boxes of the same color is(k + 1)and the maximum point is(k + 1) * (k + 1). - The recurrence relation is as follows and the maximum points will be the larger of the two cases:
a. If we removeboxes[i]first, we get(k + 1) * (k + 1) + T(i + 1, j, 0)points, where for the first term, instead of1we again get(k + 1) * (k + 1)points for removingboxes[i]due to the attached boxes to its left; and for the second term there will be no attached boxes so we have the0in this term.
b. If we decide to attachboxes[i]to some other box of the same color, sayboxes[m], then from our analyses above, the total points will beT(i + 1, m - 1, 0) + T(m, j, k + 1), where for the first term, since there is no attached boxes for subarrayboxes[i + 1, m - 1], we havek = 0for this part; while for the second term, the total number of attached boxes for subarrayboxes[m, j]will increase by1because apart from the originalkboxes, we have to account forboxes[i]now, so we havek + 1for this term. But we are not done yet. What if there are multiple boxes of the same color asboxes[i]within subarrayboxes[i + 1, j]? We have to try each of them and choose the one that yields the maximum points. Therefore the final answer for this case will be:max(T(i + 1, m - 1, 0) + T(m, j, k + 1))wherei < m <= j && boxes[i] == boxes[m].
Before we get to the actual code, it's not hard to discover that there is overlapping among the subproblems
T(i, j, k), therefore it's qualified as a DP problem and its intermediate results should be cached for future lookup. Here each subproblem is characterized by three integers (i, j, k), all of which are bounded, i.e, 0 <= i, j, k < n, so a three-dimensional array (n x n x n) will be good enough for the cache.
Finally here are the two solutions, one for top-down DP and the other for bottom-up DP. From the bottom-up solution, the time complexity will be
O(n^4) and the space complexity will be O(n^3)
Finally here are the two solutions, one for top-down DP and the other for bottom-up DP. From the bottom-up solution, the time complexity will be
O(n^4) and the space complexity will be O(n^3).Side notes: In case you are curious, for the problem "leetcode 312. Burst Balloons", the external information to subarray nums[i, j] is the two numbers (denoted as leftand right) adjacent to nums[i] and nums[j], respectively. If we absorb this extra piece of information into the definition of T(i, j), we have T(i, j, left, right)which represents the maximum coins obtained by bursting balloons of subarray nums[i, j] whose two adjacent numbers are left and right. The original problem will be T(0, n - 1, 1, 1) and the termination condition is T(i, i, left, right) = left * right * nums[i]. The recurrence relations will be: T(i, j, left, right) = max(left * nums[k] * right + T(i, k - 1, left, nums[k]) + T(k + 1, j, nums[k], right)) where i <= k <= j (here we interpret it as that the balloon at index kis the last to be burst. Since all balloons can be the last one so we try each case and choose one that yields the maximum coins). For more details, refer to dietpepsi 's postTop-down DP:public int removeBoxes(int[] boxes) {
int n = boxes.length;
int[][][] dp = new int[n][n][n];
return removeBoxesSub(boxes, 0, n - 1, 0, dp);
}
private int removeBoxesSub(int[] boxes, int i, int j, int k, int[][][] dp) {
if (i > j) return 0;
if (dp[i][j][k] > 0) return dp[i][j][k];
int res = (k + 1) * (k + 1) + removeBoxesSub(boxes, i + 1, j, 0, dp);
for (int m = i + 1; m <= j; m++) {
if (boxes[i] == boxes[m]) {
res = Math.max(res, removeBoxesSub(boxes, i + 1, m - 1, 0, dp) + removeBoxesSub(boxes, m, j, k + 1, dp));
}
}
dp[i][j][k] = res;
return res;
}X.
下面这种写法是上面解法的迭代方式,但是却有一些不同,这里我们需要对dp数组的部分值做一些初始化,将每个数字的所有k值的情况的积分都先算出来,然后在整体更新三维dp数组的时候也很有意思,并不是按照原有的顺序更新,而是块更新,先更新dp[1][0][k], dp[2][1][k], dp[3][2][k]....,再更新dp[2][0][k], dp[3][1][k], dp[4][2][k]...., 再更新dp[3][0][k], dp[4][1][k], dp[5][2][k]....,之前好像也有一道是这样区域更新的题
int removeBoxes(vector<int>& boxes) { int n = boxes.size(); int dp[n][n][n] = {0}; for (int i = 0; i < n; ++i) { for (int k = 0; k <= i; ++k) { dp[i][i][k] = (1 + k) * (1 + k); } } for (int t = 1; t < n; ++t) { for (int j = t; j < n; ++j) { int i = j - t; for (int k = 0; k <= i; ++k) { int res = (1 + k) * (1 + k) + dp[i + 1][j][0]; for (int m = i + 1; m <= j; ++m) { if (boxes[m] == boxes[i]) { res = max(res, dp[i + 1][m - 1][0] + dp[m][j][k + 1]); } } dp[i][j][k] = res; } } } return n == 0 ? 0 : dp[0][n - 1][0]; }
首先把连续相同颜色的盒子进行合并,得到数组color以及数组length,分别表示合并后盒子的颜色和长度。
dp[l][r][k]表示第l到第r个合并后的盒子,连同其后颜色为color[r]的长度k一并消去所能得到的最大得分。