Massive Algorithms: LeetCode 156 - Binary Tree Upside Down

LeetCode 156 - Binary Tree Upside Down

Tiger's leetcode solution: Binary Tree Upside Down
Given a binary tree where all the right nodes are either leaf nodes with a sibling (a left node that shares the same parent node) or empty, flip it upside down and turn it into a tree where the original right nodes turned into left leaf nodes. Return the new root.
For example:
Given a binary tree {1,2,3,4,5},

return the root of the binary tree [4,5,2,#,#,3,1].

https://yuanhsh.iteye.com/blog/2170647

Although the code for the top-down approach seems concise, it is actually subtle and there are a lot of hidden traps if you are not careful. The other approach is thinking recursively in a bottom-up fashion. If we reassign the bottom-level nodes before the upper ones, we won’t have to make copies and worry about overwriting something. We know the new root will be the left-most leaf node, so we begin the reassignment here.

http://www.cnblogs.com/grandyang/p/5172838.html
这道题让我们把一棵二叉树上下颠倒一下，而且限制了右节点要么为空要么一定会有对应的左节点。上下颠倒后原来二叉树的最左子节点变成了根节点，其对应的右节点变成了其左子节点，其父节点变成了其右子节点，相当于顺时针旋转了一下。对于一般树的题都会有迭代和递归两种解法，这道题也不例外，那么我们先来看看递归的解法。对于一个根节点来说，我们的目标是将其左子节点变为根节点，右子节点变为左子节点，原根节点变为右子节点，那么我们首先判断这个根节点是否存在，且其有没有左子节点，如果不满足这两个条件的话，直接返回即可，不需要翻转操作。那么我们不停的对左子节点调用递归函数，直到到达最左子节点开始翻转，翻转好最左子节点后，开始回到上一个左子节点继续翻转即可，直至翻转完整棵树

    TreeNode *upsideDownBinaryTree(TreeNode *root) {
        if (!root || !root->left) return root;
        TreeNode *l = root->left, *r = root->right;
        TreeNode *res = upsideDownBinaryTree(l);
        l->left = r;
        l->right = root;
        root->left = NULL;
        root->right = NULL;
        return res;
    }

http://rainykat.blogspot.com/2017/01/leetcodelinkedin-156-binary-tree-upside.html

思路1：Recursion, find the leftmost node as the root. Return repoint each new parent - root.left to previous root and root.right;
Complexity: O(N)time, O(N)space stack

Below is main rotation code of a subtree

        root->left->left = root->right;
    root->left->right = root;
    root->left = NULL;
    root->right = NULL;

The above code can be understood by following diagram –

https://zhuhan0.blogspot.com/2017/05/leetcode-156-binary-tree-upside-down.html

After the flip, root and root.right will become siblings, and the left most child will become the new root. The idea is to traverse the tree to the left. As we traverse, we make root.left the new root, root.right the left child of new root, and root itself the right child of new root.

    public TreeNode upsideDownBinaryTree(TreeNode root) {
        if(root == null || root.left == null)return root;
        TreeNode newRoot = upsideDownBinaryTree(root.left);
        //root.left is newRoot everytime
        root.left.left = root.right;
        root.left.right = root;
        root.left = null;
        root.right = null;
        return newRoot;
    }

X. Recursion 2
http://buttercola.blogspot.com/2015/10/leetcode-binary-tree-upside-down.html
The recursive solution could be bottom-up. Note that we need a parent node to save the node's parent. Also we use the return value just to store the new node.

这个题的关键是反转以后的binary tree 的 root 是以前二叉树的最左边的 leaf node. 利用这个性质，我们先一路走到最左边的那个leaf node, 并且记录一下当前节点和之前的parent node。找到这个节点以后，利用返回值一直把这个点传回来。在back tracking 的过程中，当前root 的 left child 是 parent.right. (注意要判断parent 是否为null)。如果parent == null, root.left = null; 如果没有这一句，树里面就有一个环！！root.right = parent

这个题的思路比较类似reverse linked list in recursive way.

    public TreeNode upsideDownBinaryTree(TreeNode root) {

        if (root == null) {

            return null;

}

        return upsideDownBinaryTreeHelper(root, null);

}

    private TreeNode upsideDownBinaryTreeHelper(TreeNode root, TreeNode parent) {

        if (root == null) {

            return parent;

}

        TreeNode newNode = upsideDownBinaryTreeHelper(root.left, root);

        root.left = parent == null ? null : parent.right;

        root.right = parent;

        return newNode;

}

这个属于自顶向下的方法。需要注意的是在向下走的过程中parent 其实已经被更新了，所以p.left 就不能指向parent.right, 因为 parent.right 已经在向下遍历的过程里面丢了！所以需要保存这个parent.right 这个node.

    public TreeNode upsideDownBinaryTree(TreeNode root) {

        if (root == null) {

            return null;

}

        TreeNode parent = null;

        TreeNode parentRightChild = null;

        TreeNode p = root;

        while (p != null) {

            TreeNode next = p.left;

            p.left = parentRightChild;

            parentRightChild = p.right;

            p.right = parent;

            parent = p;

            p = next;

}

        return parent;

}

http://bangbingsyb.blogspot.com/2014/11/leetcode-binary-tree-upside-down.html
http://www.danielbit.com/blog/puzzle/leetcode/leetcode-binary-tree-upside-down

http://blog.csdn.net/whuwangyi/article/details/43186045
这题有一个重要的限制就是，整个数的任何一个右孩子都不会再生枝节，基本就是一个梳子的形状。对于树类型的题目，首先可以想到一种递归的思路：把左子树继续颠倒，颠倒完后，原来的那个左孩子的左右孩子指针分别指向原来的根节点以及原来的右兄弟节点即可。

public TreeNode UpsideDownBinaryTree(TreeNode root) {
if (root == null)
return null;
TreeNode parent = root, left = root.left, right = root.right;
if (left != null) {
TreeNode ret = UpsideDownBinaryTree(left);
left.left = right;
left.right = parent;
return ret;
}
return root;
}

第二个思路是直接用迭代代替递归，做起来也不麻烦，并且效率会更高，因为省去了递归所用的栈空间。

public TreeNode UpsideDownBinaryTree(TreeNode root) {
TreeNode node = root, parent = null, right = null;
while (node != null) {
TreeNode left = node.left;
node.left = right;
right = node.right;
node.right = parent;
parent = node;
node = left;
}
return parent;
}

第三个思路比较特别，把后续遍历转换成层次遍历。注意由于Java不支持对TreeNode地址传引用，所以这里弄了一个全局变量。另外，类似于对链表的处理，这里我弄了一个dummy node简化对根节点的处理。

private TreeNode out = null;
public TreeNode UpsideDownBinaryTree(TreeNode root) {
TreeNode dummy = new TreeNode(0);
dummy.left = new TreeNode(0);
out = dummy;
postorder(root);
return dummy.right;
}
private void postorder(TreeNode root) {
if (root == null)
return;
postorder(root.left);
postorder(root.right);
if (out.left == null) {
out.left = root;
out.left.left = null;
out.left.right = null;
} else if (out.right == null) {
out.right = root;
out.right.left = null;
out.right.right = null;
}
if (out.left != null && out.right != null)
out = out.right;
}

X.
http://www.voidcn.com/article/p-sbdjxfzs-zo.html

    public TreeNode upsideDownBinaryTree(TreeNode root) {
        if(root == null || (root.left == null && root.right == null)) {
            return root;
        }
        TreeNode newRoot = upsideDown(root, root.left, root.right);
        root.left = null;
        root.right = null;
        return newRoot;
    }
    
    private TreeNode upsideDown(TreeNode root, TreeNode leftChild, TreeNode rightChild) {
        if(leftChild.left == null) {
            leftChild.left = rightChild;
            leftChild.right = root;
            return leftChild;
        }
        TreeNode curLeft = leftChild.left;
        TreeNode curRight = leftChild.right;
        leftChild.left = rightChild;
        leftChild.right = root;
        return upsideDown(leftChild, curLeft, curRight);
    }

X. Not efficient

https://segmentfault.com/a/1190000005772293

啥叫upsidedown?

    a                         b
   / \        ----->         / \
  b   c                     c   a

upsidedown的意思就是把这三个node顺时针换一下位置。
整个树最后的顶点是原树最左的孩子。
假设递归来到了a为root的这一层(如上图左)，a的左边返回了新的树根b，
注意此时b代表一个子树,c也代表一个子树
我们要把b扶持登基为根，然后c和a往哪放呢？b是一颗子树啊，人家已经有左右孩子了，容不下c和a了，分析题目给的例子，题意要把他们放到b的最右的孩子下面
把这个最右的孩子叫做rightMostNode，rightMostNode是个叶子节点没有左右孩子喔，于是我们把c拖家带口(带着他的孩子们)挂在rightMostNode的左边，把a诛九族后(为了避免形成cycle，我们只要a自己，把他的孩子(b和c)都去掉，即重新实例化一个a，左右孩子为Null)挂在他的右边，返回新的根(b的根)即可

    //返回新的树根
    public TreeNode upsideDownBinaryTree(TreeNode root) {
        if (root == null || root.left == null)
            return root;
        TreeNode newRoot = upsideDownBinaryTree(root.left);//新树根在最左
        TreeNode rightMostIterator = newRoot;//找新根的最右，挂两个旋转得来的的孩子
        while (rightMostIterator.right != null) {
            rightMostIterator = rightMostIterator.right;
        }
        rightMostIterator.left = root.right;//原右孩子拖家带口投奔新根的左边
        rightMostIterator.right = new TreeNode(root.val);//原root诛九族去右边
        return newRoot;//返回新根
    }

X. Iterative
http://wlcoding.blogspot.com/2015/03/binary-tree-upside-down.html

public TreeNode UpsideDownBinaryTree(TreeNode root) {
    TreeNode p = root, parent = null, parentRight = null;
    while (p != null) {
        TreeNode left = p.left;
        TreeNode right = p.right;
        p.left = parentRight;
        p.right = parent;
        parent = p;
        parentRight = right;
        p = left;
    }
    return parent;
}

思路2: Iterative, pre is previous root after repoint, use tmp to track the right node of previous root.
Complexity: O(N)time O(1)space

public class Solution {
    public TreeNode upsideDownBinaryTree(TreeNode root) {
        TreeNode cur = root;
        TreeNode pre = null;
        TreeNode tmp = null;
        TreeNode next = null;
        while(cur != null){
            next = cur.left;
            //need tmp to keep the previous right child
            cur.left = tmp;
            tmp = cur.right;
            
            cur.right = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
}

http://www.geeksforgeeks.org/flip-binary-tree/

Given a binary tree, the task is to flip the binary tree towards right direction that is clockwise. See below examples to see the transformation.

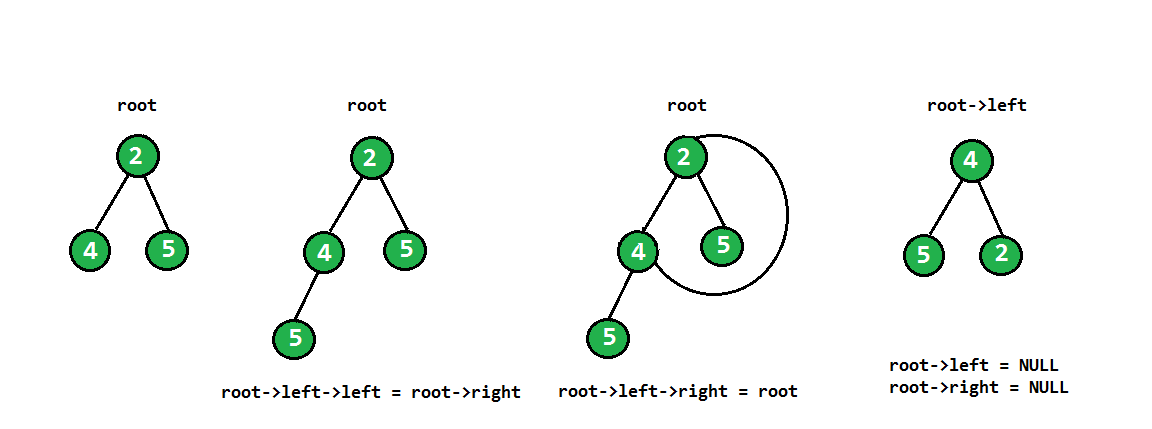
In the flip operation, left most node becomes the root of flipped tree and its parent become its right child and the right sibling become its left child and same should be done for all left most nodes recursively.

Below is main rotation code of a subtree

        root->left->left = root->right;
 root->left->right = root;
 root->left = NULL;
 root->right = NULL;

The above code can be understood by following diagram –

as we are storing root->left in flipped root, flipped subtree gets stored in each recursive call.

Node* flipBinaryTree(Node* root)

{

    // Base cases

    if (root == NULL)

        return root;

    if (root->left == NULL && root->right == NULL)

        return root;

    //  recursively call the same method

    Node* flippedRoot = flipBinaryTree(root->left);

    //  rearranging main root Node after returning

    // from recursive call

    root->left->left = root->right;

    root->left->right = root;

    root->left = root->right = NULL;

    return flippedRoot;

}

// Iterative method to do level order traversal

// line by line

void printLevelOrder(Node *root)

{

    // Base Case

    if (root == NULL)  return;

    // Create an empty queue for level order traversal

    queue<Node *> q;

    // Enqueue Root and initialize height

    q.push(root);

    while (1)

{

        // nodeCount (queue size) indicates number

        // of nodes at current lelvel.

        int nodeCount = q.size();

        if (nodeCount == 0)

            break;

        // Dequeue all nodes of current level and

        // Enqueue all nodes of next level

        while (nodeCount > 0)

{

            Node *node = q.front();

            cout << node->data << " ";

            q.pop();

            if (node->left != NULL)

                q.push(node->left);

            if (node->right != NULL)

                q.push(node->right);

            nodeCount--;

}

        cout << endl;

}

}

Read full article from Tiger's leetcode solution: Binary Tree Upside Down

LeetCode 156 - Binary Tree Upside Down

Labels

Popular Posts