LeetCode 1284 - Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/,,

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbours of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighboors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

Binary matrix is a matrix with all cells equal to 0 or 1 only.

Zero matrix is a matrix with all cells equal to 0.

Example 1:

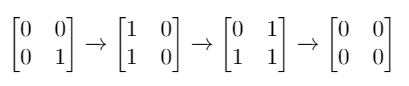
Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We don't need to change it.

Example 3:

Input: mat = [[1,1,1],[1,0,1],[0,0,0]]
Output: 6

Example 4:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix can't be a zero matrix

Constraints:

• m == mat.length
• n == mat[0].length
• 1 <= m <= 3
• 1 <= n <= 3
• mat[i][j] is 0 or 1.

https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/discuss/446306/C%2B%2B-Bit-vector-%2B-Regular-BFS

https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/discuss/446342/JavaPython-3-Convert-matrix-to-int-then-BFS-w-explanation-comments-and-analysis.

Q: Could you please further explain about the logic of transferring the matrix to int?
sum(cell << (i * n + j) for i, row in enumerate(mat) for j, cell in enumerate(row))
I wonder how it works and why it works.

A: For Input: mat = [[0,0],[0,1]], map it to 0b1000, that is, mapping mat[i][j] to the (i * n + j)th bit of an int. specifically,
mat[0][0] = 0, corresponds to 0th bit, which is 0;
mat[0][1] = 0, corresponds to 1st bit, which is 0;
mat[1][0] = 0, corresponds to 2nd bit, which is 0;
mat[1][1] = 1, corresponds to 3rd bit, which is 1;

After mapping, any operations on the binary cells of the mat are equals to the operations on the corresponding bits of the mapped int. That's why it works.

Q: Why do you use "|" to initialize the matrix and use "^" to calculate the next?

A:

1. When using 0 |= b, where b = 0 or 1, the result is b; you can change it to

start  += mat[i][j] << (i * n + j); 

2. Use next ^ 1 << k (where k = i * n + j) to flip kth bit of next, which is equal to flipping the corresponding cell (i, j) in the matrix.

end of Q & A

---

1. Since m < 3, n < 3 are given as constraints, there are at most 9 cells and an int has enough bits to store their values;
2. Map the m * n cells of the initial state of the matrix to the 0 ~ m * n - 1th bits of an int: start;
3. For each one of the m * n bits, flip it and its neighbors, then BFS to check if 0, corresponding to an all 0s matrix, is among the resulting states; if yes, return the minimum steps needed;
4. Use a Set to avoid duplicates;
5. If after the traversal of all states without finding 0, return -1.

    private static final int[] d = {0, 0, 1, 0, -1, 0};
    public int minFlips(int[][] mat) {
        int start = 0, m = mat.length, n = mat[0].length;
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                start |= mat[i][j] << (i * n + j); // convert the matrix to an int.
        Queue<Integer> q = new LinkedList<>(Arrays.asList(start));
        Set<Integer> seen = new HashSet<>(q);
        for (int step = 0; !q.isEmpty(); ++step) {
            for (int sz = q.size(); sz > 0; --sz) {
                int cur = q.poll();
                if (cur == 0) // All 0s matrix found.
                    return step;
                for (int i = 0; i < m; ++i) { // traverse all m * n bits of cur.
                    for (int j = 0; j < n; ++j) {
                        int next = cur;
                        for (int k = 0; k < 5; ++k) { // flip the cell (i, j) and its neighbors.
                            int r = i + d[k], c = j + d[k + 1];
                            if (r >= 0 && r < m && c >= 0 && c < n)
                                next ^= 1 << (r * n + c);
                        }
                        if (seen.add(next)) // seen it before ?
                            q.offer(next); // no, put it into the Queue.
                    }
                }    
            }
        }
        return -1; // impossible to get all 0s matrix.
    }

    def minFlips(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        start = sum(cell << (i * n + j) for i, row in enumerate(mat) for j, cell in enumerate(row))
        dq = collections.deque([(start, 0)])
        seen = {start}
        while dq:
            cur, step = dq.popleft()
            if not cur:
                return step
            for i in range(m):
                for j in range(n):
                    next = cur
                    for r, c in (i, j), (i, j + 1), (i, j - 1), (i + 1, j), (i - 1, j):
                        if m > r >= 0 <= c < n:
                            next ^= 1 << (r * n + c)
                    if next not in seen:
                        seen.add(next)
                        dq.append((next, step + 1))
        return -1

Analysis:
Time & Space: O(2 ^ (m * n))

X.
https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/discuss/446371/Java-Recursion-%2B-Memoization-Explained

Recursion + Memoization

In this problem, we can think in a brute manner first.
We will try to flip the element at each index of the 2D matrix once and let recursion get the answer for the flipped array.

• Now while doing this we need to take care that we don't get trapped in a cycle (I have taken care of it by using a hashset).
• For eg consider the 2D matrix given below.
  [1 0]
  [1 0]
• Initially the call will be made by flipping the (0, 0) indexed element and its neighbors according to what is given in question.
• The 2D matrix changes to :-
  [0 1]
  [0 0]
• Now this configuration of the 2D array will make a recursive call by flipping the element at index (0, 0) and its neighbors. This will again give us an array configuration we had seen before in the same recursive branh (a cycle).
  [1 0]
  [1 0]
• To avoid cycles i have used a set.
  Since the constraints of the problem are very weak, so using a string to memoize the state would not cost much on the runtime though concatenating strings is expensive.
  In this problem I have tried all possibilities of flipping all elements in a 2D array and made recursive calls to the resulting configurations. The recursive branch which brings the minimum no of steps will be a part of the solution.
  In the base case we check if all elements in the array are 0 or not.
  (BFS is another way to come up with a solution in which you will be needing a visited array(to avoid cycle) and a queue).

class Solution {
    
    public static boolean check(int[][] mat, int n, int m){
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(mat[i][j] == 1) return false;
            }
        }
        return true;
    }
    
    public static void flip(int[][] mat, int n, int m, int i, int j){
        mat[i][j] = mat[i][j] ^ 1;
        if(i - 1 >= 0) mat[i - 1][j] = mat[i - 1][j] ^ 1;
        if(j - 1 >= 0) mat[i][j - 1] = mat[i][j - 1] ^ 1;
        if(i + 1 < n) mat[i + 1][j] = mat[i + 1][j] ^ 1;
        if(j + 1 < m) mat[i][j + 1] = mat[i][j + 1] ^ 1;
    }
    
    public static int func(int[][] mat, int n, int m, HashSet<String> set, HashMap<String, Integer> dp){
        if(check(mat, n, m)) return 0;
        String t = "";
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                t += Integer.toString(mat[i][j]);
            }
        }
        
        if(dp.containsKey(t)) return dp.get(t);
        if(set.contains(t)) return Integer.MAX_VALUE;
        
        set.add(t);
        int min = Integer.MAX_VALUE;
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                flip(mat, n, m, i, j);
                int small = func(mat, n, m, set, dp);
                if(small != Integer.MAX_VALUE) min = Math.min(min, 1 + small);
                flip(mat, n, m, i, j);
            }
        }
        set.remove(t);
        dp.put(t, min);
        return min;
    }
    
    public int minFlips(int[][] mat) {
        int n = mat.length, m = mat[0].length;
        HashMap<String, Integer> dp = new HashMap<>();
        int ans = func(mat, n, m, new HashSet<>(), dp);
        return ans == Integer.MAX_VALUE ? -1 : ans;
    }

x. https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/discuss/446456/Beat-100-No-NP-hard-O((nm)3)-linear-algebra-solution

This is a simplified version of a google phone screen posted below:
https://leetcode.com/discuss/interview-question/422725/google-phone-screen-lights-out-puzzle/397815

The simplification here mainly refers to the fairly small constraints. With m and n both <=3, we can come up with brute force exponential solution.

But this is actually not a NP-hard problem in maths. Some good explanation can be found below:
https://www.youtube.com/watch?v=oCHCD_-nhg4
http://mathworld.wolfram.com/LightsOutPuzzle.html

https://www.acwing.com/solution/LeetCode/content/6856/

(枚举第一行) $O(mn\cdot 2^n)$

1. 我们发现，如果确定了第一行（或第一列）反转哪些位置，则之后反转的位置就都可以确定。
2. 假设我们已经反转了第一行的某些位置，我们从第二行开始一直到最后一行，如果发现当前位置的上一行是 1，则当前位置需要进行反转。我们在之后每一行，都去填上一行留下的坑。
3. 最后判断下最后一行是否都已经变成了 0。

时间复杂度

• 仅需要枚举第一行的方案，然后进行整体的判断，故时间复杂度为 $O(mn\cdot 2^n)$。
• 如果列数较小，行数较大，则可以枚举第一列。

空间复杂度

• 需要额外 $O(mn)$ 的空间记录中间过程。

    int minFlips(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();

        const int dx[5] = {0, 0, 1, 0, -1};
        const int dy[5] = {0, 1, 0, -1, 0};

        int ans = m * n + 1;

        for (int S = 0; S < (1 << n); S++) {
            int tot = 0;
            vector<vector<int>> tmp(m, vector<int>(n, 0));

            for (int j = 0; j < n; j++)
                if ((S >> j) & 1) {
                    tot++;

                    for (int k = 0; k < 5; k++) {
                        int tx = 0 + dx[k], ty = j + dy[k];
                        if (tx < 0 || tx >= m || ty < 0 || ty >= n)
                            continue;
                        tmp[tx][ty] ^= 1;
                    }
                }

            for (int i = 1; i < m; i++)
                for (int j = 0; j < n; j++)
                    if (mat[i - 1][j] ^ tmp[i - 1][j]) {
                        tot++;

                        for (int k = 0; k < 5; k++) {
                            int tx = i + dx[k], ty = j + dy[k];
                            if (tx < 0 || tx >= m || ty < 0 || ty >= n)
                                continue;
                            tmp[tx][ty] ^= 1;
                        }
                    }

            bool flag = true;
            for (int j = 0; j < n; j++)
                if (mat[m - 1][j] ^ tmp[m - 1][j]) {
                    flag = false;
                    break;
                }

            if (flag)
                ans = min(ans, tot);
        }

        if (ans == m * n + 1)
            ans = -1;

        return ans;
    }




(暴力枚举) $O(mn\cdot 2^{mn})$

1. 暴力枚举哪些位置需要反转，一共有 $2^{mn}$ 种方案。
2. 对于每种方案，验证最终是否为全 0。
3. 找到反转次数最少的方案。

时间复杂度

• 验证需要 $O(mn)$ 的时间复杂度，故总时间复杂度为 $O(mn\cdot 2^{mn})$。

空间复杂度

• 需要额外 $O(mn)$ 的空间，可以通过恢复现场来省略掉这部分空间

    int minFlips(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();

        const int dx[5] = {0, 0, 1, 0, -1};
        const int dy[5] = {0, 1, 0, -1, 0};

        int ans = m * n + 1;

        for (int S = 0; S < (1 << m * n); S++) {
            int tot = 0;
            vector<vector<int>> tmp(m, vector<int>(n, 0));

            for (int i = 0; i < m * n; i++)
                if ((S >> i) & 1) {
                    tot++;
                    int x = i / n, y = i % n;

                    for (int j = 0; j < 5; j++) {
                        int tx = x + dx[j], ty = y + dy[j];
                        if (tx < 0 || tx >= m || ty < 0 || ty >= n)
                            continue;
                        tmp[tx][ty] ^= 1;
                    }
                }

            bool flag = true;
            for (int i = 0; i < m && flag; i++)
                for (int j = 0; j < n && flag; j++) {
                    if (tmp[i][j] ^ mat[i][j])
                        flag = false;
                }
            if (flag)
                ans = min(ans, tot);
        }
        if (ans == m * n + 1)
            ans = -1;

        return ans;
    }