LeetCode 1259 - Handshakes That Don't Cross

https://algorithm-notes-allinone.blogspot.com/2019/11/leetcode-1259-handshakes-that-dont-cross.html
https://leetcode.com/problems/handshakes-that-dont-cross/description/

You are given an even number of people num_people that stand around a circle and each person shakes hands with someone else, so that there are num_people / 2 handshakes total.

Return the number of ways these handshakes could occur such that none of the handshakes cross.

Since this number could be very big, return the answer mod 10^9 + 7

Example 1:

Input: num_people = 2
Output: 1

Example 2:

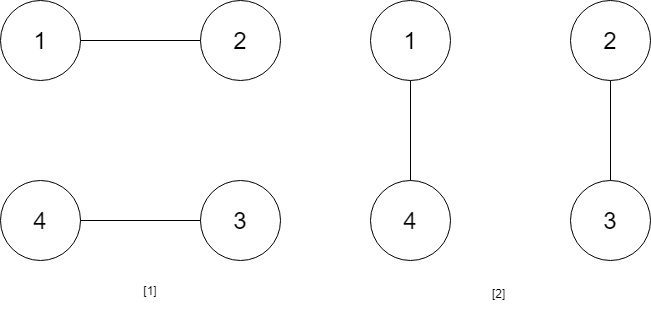
Input: num_people = 4
Output: 2
Explanation: There are two ways to do it, the first way is [(1,2),(3,4)] and the second one is [(2,3),(4,1)].

Example 3:

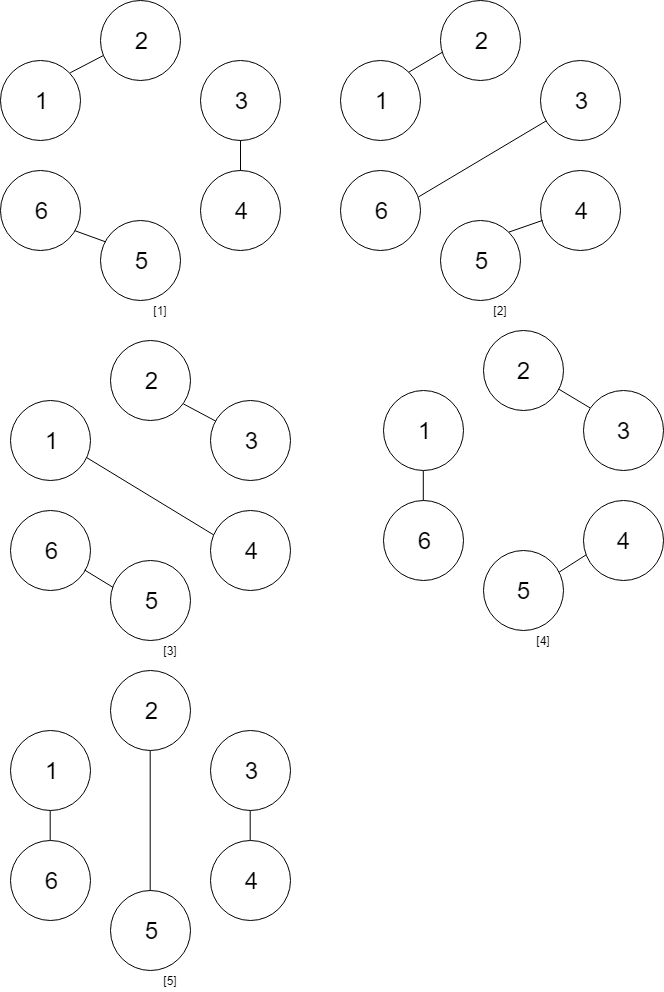
Input: num_people = 6
Output: 5

Example 4:

Input: num_people = 8
Output: 14

Constraints:

• 2 <= num_people <= 1000
• num_people % 2 == 0

This problem can be solved by dp.

Why? because, as shown in the above figures, it can be easily converted to similar questions but with smaller sizes.

Let us use dp[n] to represent the total ways for n people.

The first person can shake hands with the second one, but cannot shake hands with the second one. Why?

Because if the first person connects with the third one, then the second one have to cross the "line" to shake hands with other people.

Thus, if the first person shake hands with the jth person, this essentially divide the original circle into two parts:

one is from i+1 to the j-1 people, and the other is from j+1 to the nth people.

So we need to leave even number of people in both sides.

Thus, dp[n] = dp[0]* dp[n-2] + dp[2]*dp[n-2-2] + ... + dp[j]*dp[n-j-2].

In addition, due to symmetry, we can just calculate half of the circle.

1.     int numberOfWays(int num_people) {
2.         int n = num_people, mod = 1e9+7;
3.         vector<long> dp(n+1, 0);
4.         dp[0] = 1;
5.         for(int i=2; i<=n; i += 2) {
6.             for(int j=0; j<=i-j-2; j += 2) {//calculate half circle
7.                 if(j==i-j-2) dp[i] += dp[j]*dp[i-j-2]%mod;
8.                 else dp[i] += 2*((dp[j]%mod)*(dp[i-j-2]%mod)%mod);
9.                 dp[i] %=mod;
10. }
11.         }
12.         return dp[n];
13.     }

https://www.acwing.com/file_system/file/content/whole/index/content/150818/

(动态规划) $O(n^2)$

1. $f(i)$ 表示 i 个时的方案数，其中 i 为偶数。
2. 初始时 $f(0)=1$，其余为 0。
3. 转移时，枚举第 i 个人和编号为 j 的人握手，其中 j 为奇数，则 $f(i)=f(i)+f(j-1)\ast f(i-j-1)$。这个公式的含义是，如果第 i 个人与第 j 个人握手，则前 $j-1$ 个人的握手问题为子问题，共有 $f(j-1)$ 种方案；[j + 1, i - 1] 为 $i-j-1$ 个人握手的问题，共有 $f(i-j-1)$ 种方案，根据乘法原理和加法原理，对于每个 j，我们需要累加答案 $f(j-1)\cdot f(i-j-1)$。
4. 最终答案为 $f(n)$。

时间复杂度

• 共有 $O(n)$ 个状态，每个状态需要 $O(n)$ 的时间转移，故总时间复杂度为 $O(n^2)$。

空间复杂度

• 需要额外 $O(n)$ 的空间存储状态。

    #define LL long long
    int numberOfWays(int num_people) {
        const int mod = 1000000007;
        vector<int> f(num_people + 1, 0);
        f[0] = 1;

        for (int i = 2; i <= num_people; i += 2)
            for (int j = 1; j < i; j += 2)
                f[i] = (f[i] + (LL)(f[j - 1]) * f[i - j - 1] % mod) % mod;

        return f[num_people];
    }

https://www.cnblogs.com/wowpH/p/11880952.html

先分析一下示例 3，
第 6 个人和第 5 个人握手，圆被分成两部分，一部分是 4 个人，另一部分是 0 个人。0 个人的方案数为 1，4 个人的方案数可以递归计算为 2，所以这种情况有 2 种方案。
第 6 个人和第 3 个人握手，圆被分成两部分，每部分都是 2 个人，2 个人的方案数是 1，所以这种情况有 1 种方案。
第 6 个人和第 1 个人握手，圆被分成两部分，一部分是 0 个人，另一部分是 4 个人，所以这种情况有 2 中方案。
因此 6 个人的时候有 5 种方案数。@wowpH

有 n 个人（n为偶数），如果第 n 个人和第 i （i = n - 1, n - 3, ……，1）个人握手，那么分成的两部分中，一部分有 i - 1 人，另一部分有 n - i - 1 人。这两部分又是一个新的子问题。

所以题目可以采用 动态规划(DP) 来解决。

用大小为 num_people + 1 的 long型一维数组 arr 来保存每种人数时的方案数。公式为：

𝑎𝑟𝑟[𝑛]=⎧⎩⎨⎪⎪1∑𝑖=1𝑛−1(𝑎𝑟𝑟[𝑖−1]∗𝑎𝑟𝑟[𝑛−𝑖−1]) 𝑛=0或𝑛=2 𝑛>2，𝑛为偶数，𝑖为奇数.$$arr[n]=\{\begin{array}{ll}1& n=0或n=2\\ {\displaystyle \sum _{i=1}^{n-1}(arr[i-1]\ast arr[n-i-1])}& n>2，n为偶数，i为奇数\end{array}.$$

private static final int mod = 1000000007; private long[] arr; public int numberOfWays(int num_people) { arr = new long[num_people + 1]; return (int) dp(num_people); } private long dp(int n) { if (n == 0 || n == 2) { return 1; } long ret = 0; for (int i = n - 1; i >= 1; i -= 2) { if (arr[i - 1] == 0) { arr[i - 1] = dp(i - 1); } if (arr[n - i - 1] == 0) { arr[n - i - 1] = dp(n - i - 1); } ret += arr[i - 1] * arr[n - i - 1]; ret %= mod; } return ret; }