LeetCode 1260 - Shift 2D Grid

https://leetcode.com/problems/shift-2d-grid/

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] becomes at grid[i][j + 1].
• Element at grid[i][n - 1] becomes at grid[i + 1][0].
• Element at grid[n - 1][n - 1] becomes at grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1:

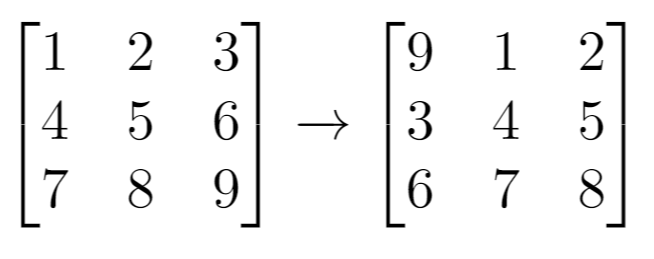
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

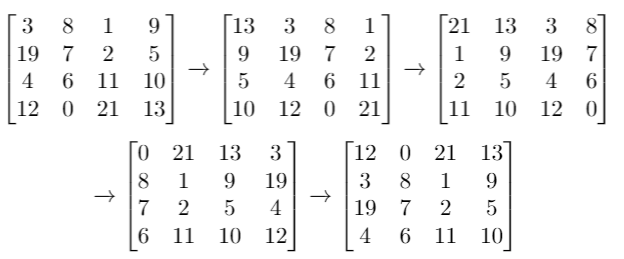
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

https://leetcode.com/problems/shift-2d-grid/discuss/431102/JavaPython-3-2-simple-codes-using-mod-space-O(m-*-n)-and-O(1).

1. Number the cells from 0 to m * n - 1;
2. In case k >= m * n, use k % (m * n) to avoid those whole cycles of m * n operations;

Method 1: space O(m * n)
Since shifting right will put the last k cells in grid on the first k cells, we start from the kth cells from last, the index of which is m * n - k % (m * n).

    public List<List<Integer>> shiftGrid(int[][] grid, int k) {
        int m = grid.length, n = grid[0].length; 
        int start = m * n - k % (m * n);
        LinkedList<List<Integer>> ans = new LinkedList<>();
        for (int i = start; i < m * n + start; ++i) {
            int j = i % (m * n), r = j / n, c = j % n;
            if ((i - start) % n == 0)
                ans.add(new ArrayList<>());
            ans.peekLast().add(grid[r][c]);
        }
        return ans;
    }

    def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        m, n = len(grid), len(grid[0])
        start = m * n - k % (m * n)
        ans = []
        for i in range(start, m * n + start):
            j = i % (m * n)
            r, c =  j // n, j % n
            if not (j - start) % n:
                ans.append([])
            ans[-1].append(grid[r][c]) 
        return ans

---

Method 2: space O(1) - excluding return list

1. Imagine the grid to be a 1-D array of size m * n;
2. reverse the whole array;
3. reverse the first k elements
4. reverse the remaing m * n - k element.

    public List<List<Integer>> shiftGrid(int[][] grid, int k) {
        int m = grid.length, n = grid[0].length;
        k %= m * n;
        reverse(grid, 0, m * n - 1);
        reverse(grid, 0, k - 1);
        reverse(grid, k, m * n - 1);
        List<List<Integer>> ans = new ArrayList<>();
        for (int[] row : grid)
            ans.add(Arrays.stream(row).boxed().collect(Collectors.toList()));
        return ans;
    }
    private void reverse(int[][] g, int lo, int hi) {
        int m = g.length, n = g[0].length;
        while (lo < hi) {
            int r = lo / n, c = lo++ % n, i = hi / n, j = hi-- % n, 
            tmp = g[r][c];
            g[r][c] = g[i][j];
            g[i][j] = tmp;
        }
    }

    def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:

        def reverse(lo: int, hi: int) -> None:
            while lo < hi:
                r, c, i, j = lo // cols, lo % cols, hi // cols, hi % cols
                grid[r][c], grid[i][j] = grid[i][j], grid[r][c]
                lo += 1
                hi -= 1

        rows, cols = len(grid), len(grid[0])
        k %= rows * cols
        reverse(0, rows * cols - 1)
        reverse(0, k - 1)
        reverse(k, rows * cols - 1)
        return grid

https://leetcode.com/problems/shift-2d-grid/discuss/431111/Simple-to-understand-java

  public static List<List<Integer>> shiftGrid(int[][] grid, int k) {
        int[][] temp = new int[grid.length][grid[0].length]; // took temp grid
        int n = grid.length;
        int m = grid[0].length;
        int mod = n * m;
        k = k % mod; // minimize the k value
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int p = j + k; // defines which col
                int r = p / (m); // defines which row
                if (p < m) {
                    temp[i][p] = grid[i][j];
                } else {
                    temp[(i + r) % n][p % m] = grid[i][j];
                }
            }
        }
  // making temp grid into list
        List<List<Integer>> result = new LinkedList<>();
        for (int[] t : temp) {
            LinkedList<Integer> c = new LinkedList<>();
            for (int i : t) {
                c.add(i);
            }
            result.add(c);
        }
        return result;
    }

https://www.cnblogs.com/wentiliangkaihua/p/11886518.html

首先是最小化k，从原理（画个2*2）可以得到k可以优化到k % (n*m).

接下来要确定每个元素要转移到的位置，首先是column因为比较简单，算当前col（j）+ k = p，然后p < m时可以直接转换temp[i][p] = grid[i][j];

如果p>m, column就要再模m，p % m = j。

然后是比较难的row，如果p < m，就可以直接用temp[i][p] = grid[i][j]

如果p>m, 根据题意我们需要把每个第一列的元素下移，最后一个元素登顶,因为最终决定位置的是列，所以最重要加的只有(j+k) / m，最后再+row（i）模n

temp[(i + r) % n][p % m] = grid[i][j];

     public static List<List<Integer>> shiftGrid(int[][] grid, int k) {
            int[][] temp = new int[grid.length][grid[0].length]; // took temp grid
            int n = grid.length;
            int m = grid[0].length;
            int mod = n * m;
            k = k % mod; // minimize the k value
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    int p = j + k; // defines which col
                    int r = p / (m); // defines which row，因为整个process是column在移动所以移动整数倍m是一样的
                    if (p < m) {
                        temp[i][p] = grid[i][j];
                    } else {
                        temp[(i + r) % n][p % m] = grid[i][j];
                    }
                }
            }
            // making temp grid into list
            List<List<Integer>> result = new LinkedList<>();
            for (int[] t : temp) {
                LinkedList<Integer> c = new LinkedList<>();
                for (int i : t) {
                    c.add(i);
                }
                result.add(c);
            }
            return result;
        }

     public static List<List<Integer>> shiftGrid(int[][] grid, int k) {
            int[][] temp = new int[grid.length][grid[0].length]; // took temp grid
            int n = grid.length;
            int m = grid[0].length;
            int mod = n * m;
            k = k % mod; // minimize the k value
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    int p = j + k; // defines which col
                    int r = p / m; // defines which row
                        temp[(i + r) % n][p % m] = grid[i][j]; 
                }
            }
            // making temp grid into list
            List<List<Integer>> result = new LinkedList<>();
            for (int[] t : temp) {
                LinkedList<Integer> c = new LinkedList<>();
                for (int i : t) {
                    c.add(i);
                }
                result.add(c);
            }
            return result;
        }

https://www.acwing.com/file_system/file/content/whole/index/content/151184/

(数学，原地算法) $O(nm)$

1. 使用额外数组的算法很基础，这里考虑不使用额外数组，且只能遍历一次整个数组。
2. 观察从 (0, 0) 位置开始的一次 k 迁移，(0, 0) 被换到 (0, k)，依次类推。如果 k 和 n*m 互质，则所有位置就都换了一次，这样的迁移仅需要常数的空间。
3. 如果 k 和 n*m 不互质，则除了从 (0, 0) 开始后，还需要从 (0, 1)，(0, 2) 等位置开始，一直到 (0, g - 1) 的位置开始迁移，其中 g 为最大公约数。
4. 虽然我们从多个位置开始了迁移，但每个位置的迁移序列都不相同，即每个位置仅会被换一次。

时间复杂度

• 求最大公约数的时间复杂度为 $O(\log (nm))$。
• 每个位置仅会被换一次，故总时间复杂度为 $O(nm)$。

空间复杂度

• 原地算法，只需要常数的额外空间。

    int gcd(int x, int y) {
        while (y) {
            int t = x % y;
            x = y;
            y = t;
        }
        return x;
    }

    vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
        int n = grid.size(), m = grid[0].size();
        int g = gcd(k, n * m);

        for (int s = 0; s < g; s++) {
            int x = s / m, y = s % m;
            int tmp = grid[x][y];

            while (1) {
                int nx = x, ny = y - k;
                while (ny < 0) {
                    nx = (nx - 1 + n) % n;
                    ny += m;
                }
                grid[x][y] = grid[nx][ny];
                if (nx == s / m && ny == s % m) {
                    grid[x][y] = tmp;
                    break;
                }
                x = nx; y = ny;
            }
        }

        return grid;
    }




https://zxi.mytechroad.com/blog/simulation/leetcode-1260-shift-2d-grid/

Solution 2: Rotate

Shift k times is equivalent to flatten the matrix and rotate by -k or (m*n – k % (m * n)).

Time complexity: O(m*n)

Space complexity: O(m*n)

  vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {  

    const int n = grid.size();

    const int m = grid[0].size();

    k = m * n - k % (m*n);

    vector<int> g;

    for (int i = 0; i < n; ++i)

      g.insert(end(g), begin(grid[i]), end(grid[i]));

    rotate(begin(g), begin(g) + k, end(g));

    auto it = begin(g);

    for (int i = 0; i < n; ++i)

      for (int j = 0; j < m; ++j)

        grid[i][j] = *it++;

    return grid;

  }

O(1) space in-place rotation

  MatrixIterator(vector<vector<int>>& data, int index = 0) :

    data_(data),

    index_(index) {}

  

  MatrixIterator& operator++() {

    ++index_;

    return *this;

  }  

  

  MatrixIterator& operator--() {

    --index_;

    return *this;

  }

  

  MatrixIterator operator +(int dis) const {

    return MatrixIterator(data_, index_ + dis);

  }

  

  MatrixIterator operator -(int dis) const {

    return MatrixIterator(data_, index_ - dis);

  }

  

  bool operator==(const MatrixIterator& o) const {

    return data_ == o.data_ && index_ == o.index_;

  }    

  

  bool operator!=(const MatrixIterator& o) const {

    return data_ != o.data_ || index_ != o.index_;

  }

  

  ptrdiff_t operator-(const MatrixIterator& o) const {

    return index_ - o.index_;

  }

  

  MatrixIterator& operator=(const MatrixIterator& o) {

    data_ = o.data_;

    index_ = o.index_;

    return *this;

  }

  

  int& operator*() {

    if (index_ <= 0) {

      return data_[0][0];

    } else if (index_ >= m() * n()) {

      return data_.back().back();

    } else {

      return data_[index_ / m()][index_ % m()];

    }

  }

  

private:

  int n() const { return data_.size(); }

  int m() const { return n() == 0 ? 0 : data_[0].size(); }  

  vector<vector<int>>& data_;

  int index_;

};

 

namespace std {

  template<>

  struct iterator_traits<MatrixIterator> {

    typedef ptrdiff_t                  difference_type;

    typedef int                        value_type;

    typedef int*                       pointer;

    typedef int&                       reference;

    typedef random_access_iterator_tag iterator_category;

  };

}

 

class Solution {

public:

  vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {  

    const int n = grid.size();

    const int m = grid[0].size();

    k = m * n - k % (m*n);

    MatrixIterator it(grid);

    rotate(it, it + k, it + m * n);

    return grid;

  }

Solution 1: Simulation

Simulate the shift process for k times.

Time complexity: O(k*n*m)

Space complexity: O(1) in-place

  vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {

    const int n = grid.size();

    const int m = grid[0].size();

    while (k--) {

      int last = grid[n - 1][m - 1];

      for (int i = n - 1; i >= 0; --i)

        for (int j = m - 1; j >= 0; --j) {          

          if (i == 0 && j == 0)

            grid[i][j] = last;

          else if (j == 0)

            grid[i][j] = grid[i - 1][m - 1];

          else

            grid[i][j] = grid[i][j - 1];

        }

      }

    return grid;

    }