Massive Algorithms: LeetCode 652 - Find Duplicate Subtrees

LeetCode 652 - Find Duplicate Subtrees

https://leetcode.com/problems/find-duplicate-subtrees/description/

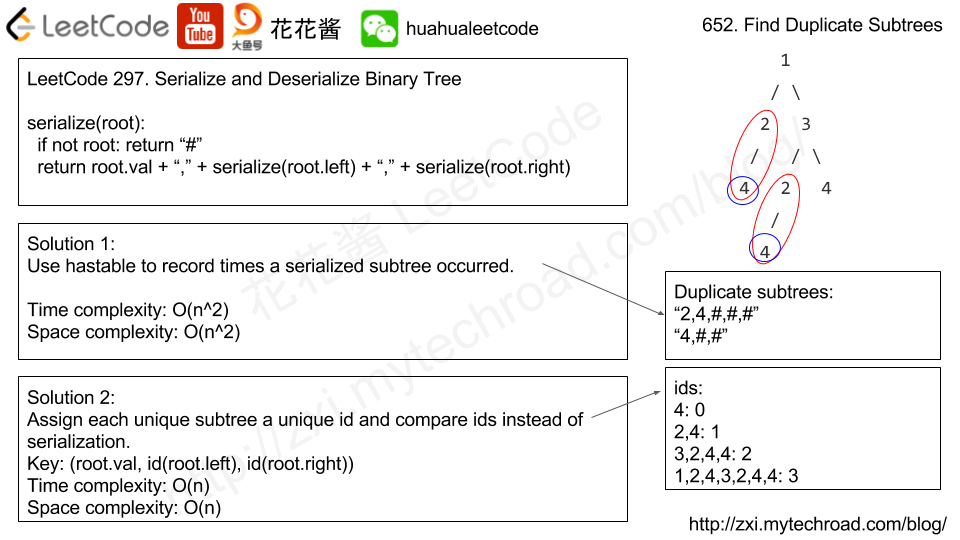
Given a binary tree, return all duplicate subtrees. For each kind of duplicate subtrees, you only need to return the root node of any oneof them.

Two trees are duplicate if they have the same structure with same node values.

Example 1:

The following are two duplicate subtrees:

      2
     /
    4

and

Therefore, you need to return above trees' root in the form of a list.

https://zxi.mytechroad.com/blog/tree/leetcode-652-find-duplicate-subtrees/

  // key -> [id, count]

  Map<Long, int[]> counts = new HashMap<>();

  List<TreeNode> ans = new ArrayList<>();

  public List<TreeNode> findDuplicateSubtrees(TreeNode root) {    

    getId(root);

    return ans;

}

  private int getId(TreeNode root) {

    if (root == null) return 0;

    long key = ((long)root.val) << 32 | getId(root.left) << 16 | getId(root.right);

    int[] id_count = counts.get(key);

    if (id_count == null) {

      id_count = new int[]{counts.size() + 1, 1};

      counts.put(key, id_count);

    } else if (++id_count[1] == 2) {

      ans.add(root);

}

    return id_count[0];

}

X.

https://leetcode.com/articles/find-duplicate-subtrees/

Time Complexity: O(N^2), where NN is the number of nodes in the tree. We visit each node once, but each creation of serial may take O(N)O(N) work.

Space Complexity: O(N^2) the size of count.
https://discuss.leetcode.com/topic/97584/java-concise-postorder-traversal-solution

public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
    List<TreeNode> res = new LinkedList<>();
    postorder(root, new HashMap<>(), res);
    return res;
}

public String postorder(TreeNode cur, Map<String, Integer> map, List<TreeNode> res) {
    if (cur == null) return "#";  
    String serial = cur.val + "," + postorder(cur.left, map, res) + "," + postorder(cur.right, map, res);
    if (map.getOrDefault(serial, 0) == 1) res.add(cur);
    map.put(serial, map.getOrDefault(serial, 0) + 1);
    return serial;
}

X.
https://leetcode.com/problems/find-duplicate-subtrees/discuss/106016/O(n)-time-and-space-lots-of-analysis
https://discuss.leetcode.com/topic/97625/o-n-time-and-space-lots-of-analysis
Approach #2: Unique Identifier [Accepted]

Intuition

Suppose we have a unique identifier for subtrees: two subtrees are the same if and only if they have the same id.

Then, for a node with left child id of x and right child id of y, (node.val, x, y) uniquely determines the tree.

Algorithm

If we have seen the triple (node.val, x, y) before, we can use the identifier we've remembered. Otherwise, we'll create a new one.

Time Complexity: $O(N)$ , where $N$ is the number of nodes in the tree. We visit each node once.
Space Complexity: $O(N)$ . Every structure we use is using $O(1)$ storage per node.

int t;

Map<String, Integer> trees;

Map<Integer, Integer> count;

List<TreeNode> ans;

public List<TreeNode> findDuplicateSubtrees(TreeNode root) {

t = 1;

trees = new HashMap();

count = new HashMap();

ans = new ArrayList();

lookup(root);

return ans;

}

public int lookup(TreeNode node) {

if (node == null)

return 0;

String serial = node.val + "," + lookup(node.left) + "," + lookup(node.right);

int uid = trees.computeIfAbsent(serial, x -> t++);

count.put(uid, count.getOrDefault(uid, 0) + 1);

if (count.get(uid) == 2)

ans.add(node);

return uid;

}

https://leetcode.com/problems/find-duplicate-subtrees/discuss/106030/Python-O(N)-Merkle-Hashing-Approach

e'll assign every subtree a unique merkle hash. You can find more information about Merkle tree hashing here: https://discuss.leetcode.com/topic/88520/python-straightforward-with-explanation-o-st-and-o-s-t-approaches

def findDuplicateSubtrees(self, root):
    from hashlib import sha256
    def hash_(x):
        S = sha256()
        S.update(x)
        return S.hexdigest()

    def merkle(node):
        if not node:
            return '#'
        m_left = merkle(node.left)
        m_right = merkle(node.right)
        node.merkle = hash_(m_left + str(node.val) + m_right)
        count[node.merkle].append(node)
        return node.merkle

    count = collections.defaultdict(list)
    merkle(root)
    return [nodes.pop() for nodes in count.values() if len(nodes) >= 2]

X. O(N^2)
https://leetcode.com/articles/find-duplicate-subtrees/

We can serialize each subtree. For example, the tree

can be represented as the serialization 1,2,#,#,3,4,#,#,5,#,#, which is a unique representation of the tree.

Perform a depth-first search, where the recursive function returns the serialization of the tree. At each node, record the result in a map, and analyze the map after to determine duplicate subtrees.

Time Complexity: $O(N^2)$ , where $N$ is the number of nodes in the tree. We visit each node once, but each creation of serial may take $O(N)$ work.
Space Complexity: $O(N^2)$ , the size of count

Map<String, Integer> count;

List<TreeNode> ans;

public List<TreeNode> findDuplicateSubtrees(TreeNode root) {

count = new HashMap();

ans = new ArrayList();

collect(root);

return ans;

}

public String collect(TreeNode node) {

if (node == null)

return "#";

String serial = node.val + "," + collect(node.left) + "," + collect(node.right);

count.put(serial, count.getOrDefault(serial, 0) + 1);

if (count.get(serial) == 2)

ans.add(node);

return serial;

}

https://discuss.leetcode.com/topic/97592/verbose-java-solution-tree-traversal

    Map<String, TreeNode> map = new HashMap<>();
    
    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
        List<TreeNode> result = new ArrayList<>();
        if (root == null) return result;
        
        traverse(first(root));
        
        for (TreeNode node : map.values()) {
            if (node != null) {
                result.add(node);
            }
        }
        
        return result;
    }
    
    private TreeNode first(TreeNode root) {
        if (root == null) return null;
        if (root.left != null && root.right != null) return root;
        if (root.left != null) return first(root.left);
        return first(root.right);
    }
    
    private void traverse(TreeNode root) {
        if (root == null) return;
        
        String s = path(root);
        if (map.containsKey(s)) {
            map.put(s, root);
        }
        else {
            map.put(s, null);
        }
        
        traverse(root.left);
        traverse(root.right);
    }
    
    private String path(TreeNode root) {
        if (root == null) return "#";
        return root.val + "," + path(root.left) + "," + path(root.right);
    }

https://www.geeksforgeeks.org/check-binary-tree-contains-duplicate-subtrees-size-2/

While the worst case performance of Approach 1 might be O(N^2), maybe it might help to point out that the average performace (both time and space) would be O(N Log N)

The easiest proof of this is by comparing it to merge sort. Despite each recursion doing O(N) work, thanks to the number of recursions being capped at Log N, the time complexity works out to be O(N Log N).

The exact same argument holds here. On an average, the height of the tree will be Log N (worst case would be where it's essentially a linked list which will lead to N^2). Both the amount of work done in serialising and the space used at each level can be represented as:

(2-1) * (N/2) + (4-1) * (N/4) + (8-1) * (N/8) + ... (N-1) * 1

Where (2-1), (4-1)... is the number of nodes being serialised at each level, and N/2, N/4... is the number of nodes at that level. If we ignore the -1s to simplify this, it simply boils down to:

2*(N/2) + 4*(N/4) + ... Log N times (since Log N is the average height)
or simply put, average performance is O(N Log N)

On a similar note, Approach 2's complexity is not strictly O(N), but somewhere between O(N) and O(N Log N), but should not get any worse than that.

If say N were close to int.MaxValue (or really even long.MaxValue depending on how generically we're analysing this), then uids assigned will necessarily have to span the whole range from 0 to MaxValue. With each iteration, uid is serialised, and the length of a serialised number is proportional to log N (strictly speaking in base 10, but that can be considered a constant and ignored). With a large enough N, a non-trivial number of recursions will have to stringify uids that get larger and larger, pushing the performance to O(N Log N)

TODO: https://leetcode.com/problems/find-duplicate-subtrees/discuss/106016/O(n)-time-and-space-lots-of-analysis

LeetCode 652 - Find Duplicate Subtrees

Labels

Popular Posts