Set Cover Problem | Set 1 (Greedy Approximate Algorithm) - GeeksforGeeks
Given a universe U of n elements, a collection of subsets of U say S = {S1, S2…,Sm} where every subset Si has an associated cost. Find a minimum cost subcollection of S that covers all elements of U.
Another example: Consider General Motors needs to buy a certain amount of varied supplies and there are suppliers that offer various deals for different combinations of materials (Supplier A: 2 tons of steel + 500 tiles for $x; Supplier B: 1 ton of steel + 2000 tiles for $y; etc.). You could use set covering to find the best way to get all the materials while minimizing cost
Source: http://math.mit.edu/~goemans/18434S06/setcover-tamara.pdf
http://ideone.com/hUY3Am
https://en.wikipedia.org/wiki/Set_cover_problem
Given a set of elements 
(called the universe) and a collection 
of 
sets whose union equals the universe, the set cover problem is to identify the smallest sub-collection of whose union equals the universe. For example, consider the universe 
and the collection of sets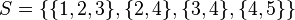 
. Clearly the union of is 
. However, we can cover all of the elements with the following, smaller number of sets: 
.
There is a greedy algorithm for polynomial time approximation of set covering that chooses sets according to one rule: at each stage, choose the set that contains the largest number of uncovered elements.
Read full article from Set Cover Problem | Set 1 (Greedy Approximate Algorithm) - GeeksforGeeks
Given a universe U of n elements, a collection of subsets of U say S = {S1, S2…,Sm} where every subset Si has an associated cost. Find a minimum cost subcollection of S that covers all elements of U.
Let U be the universe of elements, {S1, S2, … Sm} be collection of subsets of U and Cost(S1), C(S2), … Cost(Sm) be costs of subsets.
1) Let I represents set of elements included so far. Initialize I = {}
2) Do following while I is not same as U.
a) Find the set Si in {S1, S2, ... Sm} whose cost effectiveness is
smallest, i.e., the ratio of cost C(Si) and number of newly added
elements is minimum.
Basically we pick the set for which following value is minimum.
Cost(Si) / |Si - I|
b) Add elements of above picked Si to I, i.e., I = I U Si
Set Cover is NP-Hard:
There is no polynomial time solution available for this problem as the problem is a known NP-Hard problem. There is a polynomial time Greedy approximate algorithm, the greedy algorithm provides a Logn approximate algorithm.
There is no polynomial time solution available for this problem as the problem is a known NP-Hard problem. There is a polynomial time Greedy approximate algorithm, the greedy algorithm provides a Logn approximate algorithm.
2-Approximate Greedy Algorithm:
Let U be the universe of elements, {S1, S2, … Sm} be collection of subsets of U and Cost(S1), C(S2), … Cost(Sm) be costs of subsets.
Let U be the universe of elements, {S1, S2, … Sm} be collection of subsets of U and Cost(S1), C(S2), … Cost(Sm) be costs of subsets.
1) Let I represents set of elements included so far. Initialize I = {}
2) Do following while I is not same as U.
a) Find the set Si in {S1, S2, ... Sm} whose cost effectiveness is
smallest, i.e., the ratio of cost C(Si) and number of newly added
elements is minimum.
Basically we pick the set for which following value is minimum.
Cost(Si) / |Si - I|
b) Add elements of above picked Si to I, i.e., I = I U Si
Another example: Consider General Motors needs to buy a certain amount of varied supplies and there are suppliers that offer various deals for different combinations of materials (Supplier A: 2 tons of steel + 500 tiles for $x; Supplier B: 1 ton of steel + 2000 tiles for $y; etc.). You could use set covering to find the best way to get all the materials while minimizing cost
Source: http://math.mit.edu/~goemans/18434S06/setcover-tamara.pdf
http://ideone.com/hUY3Am
public static void main(final String[] args) {
final Set<Integer> unv = new HashSet<>();
unv.add(1);
unv.add(2);
unv.add(3);
unv.add(4);
unv.add(5);
final Set<Integer> s1 = new HashSet<>();
s1.add(4);
s1.add(1);
s1.add(3);
final Set<Integer> s2 = new HashSet<>();
s2.add(2);
s2.add(5);
final Set<Integer> s3 = new HashSet<>();
s3.add(1);
s3.add(4);
s3.add(3);
s3.add(2);
final Set sets[] = {s1, s2, s3};
final Map<Set, Integer> costs = new HashMap<>();
costs.put(s1, 5);
costs.put(s2, 10);
costs.put(s3, 30);
System.out.println(minCostCollection(unv, sets, costs, new ArrayList<Set>(), sets.length - 1));
}
public static int minCostCollection(final Set<Integer> unv, final Set<Integer>[] sets,
final Map<Set, Integer> costs, final List<Set> list, final int pos) {
if (unv.size() == 0) {
int cost = 0;
for (final Set s : list) {
cost = cost + costs.get(s);
}
return cost;
}
if (pos < 0) {
return Integer.MAX_VALUE;
}
final Set<Integer> unvCopy = new HashSet<>(unv);
final List<Set> list1 = new ArrayList<>(list);
list.add(sets[pos]);
for (final Integer elem : sets[pos]) {
unv.remove(elem);
}
final int cost1 = minCostCollection(unv, sets, costs, list, pos - 1);
final int cost2 = minCostCollection(unvCopy, sets, costs, list1, pos - 1);
return Math.min(cost1, cost2);
}
http://math.mit.edu/~goemans/18434S06/setcover-tamara.pdfhttps://en.wikipedia.org/wiki/Set_cover_problem
The set cover problem is a classical question in combinatorics, computer science and complexity theory. It is one of Karp's 21 NP-complete problems shown to be NP-complete in 1972.
(called the universe) and a collection of sets whose union equals the universe, the set cover problem is to identify the smallest sub-collection of whose union equals the universe. For example, consider the universe and the collection of sets 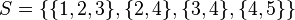. Clearly the union of is . However, we can cover all of the elements with the following, smaller number of sets: .There is a greedy algorithm for polynomial time approximation of set covering that chooses sets according to one rule: at each stage, choose the set that contains the largest number of uncovered elements.
Read full article from Set Cover Problem | Set 1 (Greedy Approximate Algorithm) - GeeksforGeeks
