LeetCode 11 - Container With Most Water
LeetCode 42 - Trapping Rain Water
https://leetcode.com/problems/trapping-rain-water-ii/
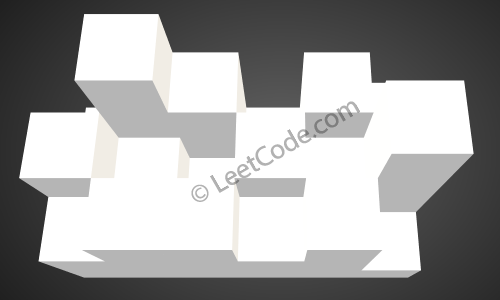
The above image represents the elevation map
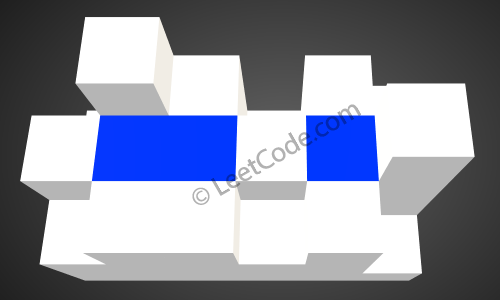
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.
X. BFS + PriorityQueue
https://zhuanlan.zhihu.com/p/33590149
https://github.com/shawnfan/LintCode/blob/master/Java/Trapping%20Rain%20Water%20II.java
https://discuss.leetcode.com/topic/60371/java-version
http://yuancrackcode.com/2015/10/21/trapping-rain-water-ii/
http://www.cnblogs.com/easonliu/p/4743644.html
http://wxx5433.github.io/trapping-rain-water.html
Thoughts: same idea as the trap Rain Water I.
Since this is not 1-way run through a 1D array (2D array can go 4 directions...), need to mark visted spot.
Use PriorityQueue, sort lowest on top, because the lowest surroundings determines the best we can get.
Bukkit theory: the lowest bar determines the height of the bukkit water. So, we always process the lowest first.
Therefore, we use a min-heap, a natural order priorityqueue based on height.
Note: when adding a new block into the queue, comparing with the checked origin, we still want to add the higher height into queue.
(The high bar will always exist and hold the bukkit.)
Step:
1. Create Cell (x,y,h)
2. Priorityqueue on Cell of all 4 borders
3. Process each element in queue, and add surrounding blocks into queue.
4. Mark checked block
O(mn*(logm+logn)) time
O(mn) space
用PriorityQueue把选中的height排序。为走位,create class Cell {x,y, height}.
注意几个理论:
1. 从matrix四周开始考虑,发现matrix能Hold住的水,取决于height低的block。
2. 必须从外围开始考虑,因为水是被包裹在里面,外面至少需要现有一层。
以上两点就促使我们用min-heap: 也就是natural order的PriorityQueue<Cell>.
process的时候,画个图也可以搞清楚,就是四个方向都走走,用curr cell的高度减去周围cell的高度。 若大于零,那么就有积水。
每个visited的cell都要mark. 去到4个方向的cell,加进queue里面继续process.
这里,有一点,和trapping water I 想法一样。刚刚从外围,只是能加到跟外围cell高度一致的水平面。往里面,很可能cell高度变化。
这里要附上curr cell 和 move-to cell的最大高度。
https://discuss.leetcode.com/topic/60418/java-solution-using-priorityqueue
http://bookshadow.com/weblog/2016/09/25/leetcode-trapping-rain-water-ii/
X.
https://discuss.leetcode.com/topic/60387/alternative-approach-using-dijkstra-in-o-rc-max-log-r-log-c-time
https://discuss.leetcode.com/topic/60693/why-reinvent-the-wheel-an-easy-understood-commented-solution-based-on-trapping-rain-1/
LeetCode 42 - Trapping Rain Water
https://leetcode.com/problems/trapping-rain-water-ii/
Given an
m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.
Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.
Example:
Given the following 3x6 height map: [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ] Return 4.

The above image represents the elevation map
[[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.
https://zhuanlan.zhihu.com/p/33590149
第一题是Leetcode 407. Trapping Rain Water II. 这道题的简单版本是Leetcode 42. Trapping Rain Water. 42的代码可以看这个discussion。下面简单说一下407的解法,思路来源于这个discussion。
对于一维来说,当我们从两个端点往中间走的时候,水位一定是单调不递减的。因为[x1, x2]之间的水位,一定是大于等于min(height[x1], height[x2])的。如果x1, x2之间有更低的bar,则不影响水位,如果有更高的bar,那么只会让水位上涨。因此当我们从两头往中间走的时候,可以一直更新当前的水位,并且计算当前经过的位置所能积蓄的水量。
对于二维来说,一个重要的注意点就是我们不再是从两个端点走,而是要更新一二维平面里的边界,而且这个边界不一定是标准的矩形,而可能是任意的多边形。因此我们每次都要找到当前边界里最低的那个点X,依据X的高度更新水位高度,并且找到它周围没有被计算过的邻居。这些邻居具备两个特质:1.他们如果可以储水,那么水位的高度一定是当前水位的高度。2. 将X移出边界后,这些邻居成为了新的边界的一部分。对于如何找当前边界里高度最低的点,我们可以将边界里的所有点都保存一个priority_queue中。看一下hermits的代码。
https://github.com/shawnfan/LintCode/blob/master/Java/Trapping%20Rain%20Water%20II.java
https://discuss.leetcode.com/topic/60371/java-version
http://yuancrackcode.com/2015/10/21/trapping-rain-water-ii/
http://www.cnblogs.com/easonliu/p/4743644.html
http://wxx5433.github.io/trapping-rain-water.html
Thoughts: same idea as the trap Rain Water I.
Since this is not 1-way run through a 1D array (2D array can go 4 directions...), need to mark visted spot.
Use PriorityQueue, sort lowest on top, because the lowest surroundings determines the best we can get.
Bukkit theory: the lowest bar determines the height of the bukkit water. So, we always process the lowest first.
Therefore, we use a min-heap, a natural order priorityqueue based on height.
Note: when adding a new block into the queue, comparing with the checked origin, we still want to add the higher height into queue.
(The high bar will always exist and hold the bukkit.)
Step:
1. Create Cell (x,y,h)
2. Priorityqueue on Cell of all 4 borders
3. Process each element in queue, and add surrounding blocks into queue.
4. Mark checked block
O(mn*(logm+logn)) time
O(mn) space
用PriorityQueue把选中的height排序。为走位,create class Cell {x,y, height}.
注意几个理论:
1. 从matrix四周开始考虑,发现matrix能Hold住的水,取决于height低的block。
2. 必须从外围开始考虑,因为水是被包裹在里面,外面至少需要现有一层。
以上两点就促使我们用min-heap: 也就是natural order的PriorityQueue<Cell>.
process的时候,画个图也可以搞清楚,就是四个方向都走走,用curr cell的高度减去周围cell的高度。 若大于零,那么就有积水。
每个visited的cell都要mark. 去到4个方向的cell,加进queue里面继续process.
这里,有一点,和trapping water I 想法一样。刚刚从外围,只是能加到跟外围cell高度一致的水平面。往里面,很可能cell高度变化。
这里要附上curr cell 和 move-to cell的最大高度。
https://discuss.leetcode.com/topic/60418/java-solution-using-priorityqueue
Your idea is interesting because it maintains a boundary.
This solution is also correct because of the invariant: the boundary is always in the queue.
One tricky case that this solution handles very well is :
9 9 9 9 9 9 8 9 9 9 9
9 0 0 0 0 0 1 0 0 0 9
9 0 0 0 0 0 0 0 0 0 9
9 0 0 0 0 0 0 0 0 0 9
9 9 9 9 9 9 9 9 9 9 9
9 0 0 0 0 0 1 0 0 0 9
9 0 0 0 0 0 0 0 0 0 9
9 0 0 0 0 0 0 0 0 0 9
9 9 9 9 9 9 9 9 9 9 9
After you process 8, the downward 1 will be replaced as 8, instead of 1 as height.
- You could write
compareTomethod in Cell, In this way, you don't need to writecomparemethod for PriorityQueue.
public class Cell {
int row;
int col;
int height;
public Cell(int row, int col, int height) {
this.row = row;
this.col = col;
this.height = height;
}
}
public int trapRainWater(int[][] heights) {
if (heights == null || heights.length == 0 || heights[0].length == 0)
return 0;
PriorityQueue<Cell> queue = new PriorityQueue<>(1, new Comparator<Cell>(){
public int compare(Cell a, Cell b) {
return a.height - b.height;
}
});
int m = heights.length;
int n = heights[0].length;
boolean[][] visited = new boolean[m][n];
// Initially, add all the Cells which are on borders to the queue.
for (int i = 0; i < m; i++) {
visited[i][0] = true;
visited[i][n - 1] = true;
queue.offer(new Cell(i, 0, heights[i][0]));
queue.offer(new Cell(i, n - 1, heights[i][n - 1]));
}
for (int i = 0; i < n; i++) {
visited[0][i] = true;
visited[m - 1][i] = true;
queue.offer(new Cell(0, i, heights[0][i]));
queue.offer(new Cell(m - 1, i, heights[m - 1][i]));
}
// from the borders, pick the shortest cell visited and check its neighbors:
// if the neighbor is shorter, collect the water it can trap and update its height as its height plus the water trapped
// add all its neighbors to the queue.
int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int res = 0;
while (!queue.isEmpty()) {
Cell cell = queue.poll();
for (int[] dir : dirs) {
int row = cell.row + dir[0];
int col = cell.col + dir[1];
if (row >= 0 && row < m && col >= 0 && col < n && !visited[row][col]) {
visited[row][col] = true;
res += Math.max(0, cell.height - heights[row][col]);
queue.offer(new Cell(row, col, Math.max(heights[row][col], cell.height)));
}
}
}
return res;
}http://bookshadow.com/weblog/2016/09/25/leetcode-trapping-rain-water-ii/
记矩形的高度、宽度分别为m, n,令二维数组peakMap[i][j] = ∞,表示矩形区域最多可以达到的水面高度
将矩形的四条边中的各点坐标加入队列q,并将各点对应的高度赋值给peakMap相同坐标
每次从q中弹出队头元素x, y,探索其上、下、左、右四个方向nx, ny:
尝试用max(peakMap[x][y], heightMap[nx][ny]) 更新 peakMap[nx][ny] 的当前值(取两者中的较小值)
X.
蓄积雨水的单元格存在两种情况:
1. 单元格的高度严格小于其上、下、左、右方向的4个单元格高度
2. 单元格的高度小于或等于其上、下、左、右方向的4个单元格高度
对于情况1,可以利用“木桶原理”将其高度调整为四周单元格中的最小高度
对于情况2,可以通过DFS,寻找与其邻接的等高节点的四周高度的最小值
private int m, n;
private int[][] heightMap;
private int dx[] = {1, 0, -1, 0};
private int dy[] = {0, 1, 0, -1};
private class Pair {
public int x, y;
public Pair(int x, int y) {
this.x = x;
this.y = y;
}
public int hashCode() {
return x + y;
}
public boolean equals(Object o) {
if (o instanceof Pair) {
Pair p = (Pair)o;
return x == p.x && y == p.y;
}
return false;
}
}
public int trapRainWater(int[][] heightMap) {
this.heightMap = heightMap;
m = heightMap.length;
n = m == 0 ? 0 : heightMap[0].length;
int sum0 = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sum0 += heightMap[i][j];
}
}
LinkedList<Pair> queue = new LinkedList<Pair>();
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (minNeighborHeight(i, j) >= heightMap[i][j]) {
queue.add(new Pair(i, j));
}
}
}
while (!queue.isEmpty()) {
Pair head = queue.removeFirst();
int i = head.x, j = head.y;
HashSet<Pair> vs = new HashSet<Pair>();
vs.add(head);
int minh = solve(i, j, vs);
if (minh > heightMap[i][j]) {
queue.add(head);
for (Pair e : vs) {
heightMap[e.x][e.y] = minh;
}
}
}
int sum1 = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sum1 += heightMap[i][j];
}
}
return sum1 - sum0;
}
private int minNeighborHeight(int i, int j) {
int minh = Integer.MAX_VALUE;
for (int k = 0; k < dx.length; k++) {
int di = i + dx[k];
int dj = j + dy[k];
minh = Math.min(minh, heightMap[di][dj]);
}
return minh;
}
private int solve(int i, int j, HashSet<Pair> vs) {
int height = heightMap[i][j];
if (i == 0 || j == 0 || i == m - 1 || j == n - 1) {
return height;
}
int minh = minNeighborHeight(i, j);
if (minh != height) {
return minh;
}
minh = Integer.MAX_VALUE;
for (int k = 0; k < dx.length; k++) {
int di = i + dx[k];
int dj = j + dy[k];
Pair pair = new Pair(di, dj);
if (vs.contains(pair)) {
continue;
}
if (heightMap[di][dj] == height) {
vs.add(pair);
minh = Math.min(minh, solve(di, dj, vs));
} else {
minh = Math.min(minh, heightMap[di][dj]);
}
}
return minh;
}https://discuss.leetcode.com/topic/60387/alternative-approach-using-dijkstra-in-o-rc-max-log-r-log-c-time
This problem can also be solved in a more general approach way using Dijkstra.
Construct a graph
V = all cells plus a dummy vertex,
If
Add an edge with zero weight from any boundary cell to the dummy vertex
G = (V, E) as follows:V = all cells plus a dummy vertex,
v, corresponding to the outside region.If
cell(i, j) is adjacent to cell(i', j'), then add an direct edge from (i, j) to (i', j') with weight height(i', j').Add an edge with zero weight from any boundary cell to the dummy vertex
v.
The weight of a path is defined as the weight of the heaviest edge along it. Then, for any cell
(i, j), the height of water it can save is equal to the weight, denoted by dist(i, j), of the shortest path from (i, j) to v. (If the weight is less than or equal to height(i, j), no water can be accumulated at that particular position.)
We want to compute the
dist(i, j) for all pairs of (i, j). Here, we have multiple sources and one destination, but this problem essentially can be solved using one pass of Dijkstra algorithm if we reverse the directions of all edges. The graph is sparse, i.e., there are O(rc) edges, resulting an O(rc log(rc)) = O(rc max(log r, log c)) runtime and using O(rc) space.
Basically, for each single cell, we need to know that for all the possible paths to outside world (where the water will escape to), what is the minimum of all path's weight, and the path's weight should be defined as the highest height value along the path.
int[] dx = {0, 0, 1, -1};
int[] dy = {1, -1, 0, 0};
List<int[]>[] g;
int start;
private int[] dijkstra() {
int[] dist = new int[g.length];
Arrays.fill(dist, Integer.MAX_VALUE / 2);
dist[start] = 0;
TreeSet<int[]> tree = new TreeSet<>((u, v) -> u[1] == v[1] ? u[0] - v[0] : u[1] - v[1]);
tree.add(new int[]{start, 0});
while (!tree.isEmpty()) {
int u = tree.first()[0], d = tree.pollFirst()[1];
for (int[] e : g[u]) {
int v = e[0], w = e[1];
if (Math.max(d, w) < dist[v]) {
tree.remove(new int[]{v, dist[v]});
dist[v] = Math.max(d, w);
tree.add(new int[]{v, dist[v]});
}
}
}
return dist;
}
public int trapRainWater(int[][] a) {
if (a == null || a.length == 0 || a[0].length == 0) return 0;
int r = a.length, c = a[0].length;
start = r * c;
g = new List[r * c + 1];
for (int i = 0; i < g.length; i++) g[i] = new ArrayList<>();
for (int i = 0; i < r; i++)
for (int j = 0; j < c; j++) {
if (i == 0 || i == r - 1 || j == 0 || j == c - 1) g[start].add(new int[]{i * c + j, 0});
for (int k = 0; k < 4; k++) {
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < r && y >= 0 && y < c) g[i * c + j].add(new int[]{x * c + y, a[i][j]});
}
}
int ans = 0;
int[] dist = dijkstra();
for (int i = 0; i < r; i++)
for (int j = 0; j < c; j++) {
int cb = dist[i * c + j];
if (cb > a[i][j]) ans += cb - a[i][j];
}
return ans;
}Basic physics:
Unlike bricks, water flows to wherever it could.
i.e we can't have the follwoing config made with water, but can do it with bricks
000
010
000
In the case above, if the "1" is built with water, that water can't stay. It needs to be spilled!
2 steps Algorithm:
1. Since we know how to trap rain water in 1d, we can just transfor this 2D problem into 2 1D problems
we go row by row, to calculate each spot's water
we go column by column, to calculate each spot's water
2. Then, here comes the meat,
For every spot that gets wet, from either row or column calculation, the water can possibly spill.
We need to check the water height aganist it's 4 neighbors.
If the water height is taller than any one of its 4 neightbors, we need to spill the extra water.
If we spill any water from any slot, then its 4 neightbors needs to check themselves again.
For example, if we spill some water in the current slot b/c its bottm neighbor's height, current slot's top neighbor's height might need to be updated again.
we keep checking until there is no water to be spilled.
*/
public class Solution {
public int trapRainWater(int[][] heightMap) {
/*FIRST STEP*/
if(heightMap.length == 0) return 0;
int[][] wetMap = new int[heightMap.length][heightMap[0].length];
int sum = 0;
/*row by row*/
for(int i = 1; i < wetMap.length - 1; i++){
wetMap[i] = calculate(heightMap[i]);
}
/*column by column*/
for(int i = 1; i < heightMap[0].length - 1; i++){
int[] col = new int[heightMap.length];
for(int j = 0; j < heightMap.length; j++){
col[j] = heightMap[j][i];
}
int[] colResult = calculate(col);
/*update the wetMap to be the bigger value between row and col, later we can spill, don't worry*/
for(int j = 0; j < heightMap.length; j++){
wetMap[j][i] = Math.max(colResult[j], wetMap[j][i]);
sum += wetMap[j][i];
}
}
/*SECOND STEP*/
boolean spillWater = true;
int[] rowOffset = {-1,1,0,0};
int[] colOffset = {0,0,1,-1};
while(spillWater){
spillWater = false;
for(int i = 1; i < heightMap.length - 1; i++){
for(int j = 1; j < heightMap[0].length - 1; j++){
/*If this slot has ever gotten wet, exammine its 4 neightbors*/
if(wetMap[i][j] != 0){
for(int m = 0; m < 4; m++){
int neighborRow = i + rowOffset[m];
int neighborCol = j + colOffset[m];
int currentHeight = wetMap[i][j] + heightMap[i][j];
int neighborHeight = wetMap[neighborRow][neighborCol] +
heightMap[neighborRow][neighborCol];
if(currentHeight > neighborHeight){
int spilledWater = currentHeight - Math.max(neighborHeight, heightMap[i][j]);
wetMap[i][j] = Math.max(0, wetMap[i][j] - spilledWater);
sum -= spilledWater;
spillWater = true;
}
}
}
}
}
}
return sum;
}
/*Nothing interesting here, the same function for trapping water 1*/
private int[] calculate (int[] height){
int[] result = new int[height.length];
Stack<Integer> s = new Stack<Integer>();
int index = 0;
while(index < height.length){
if(s.isEmpty() || height[index] <= height[s.peek()]){
s.push(index++);
}else{
int bottom = s.pop();
if(s.size() != 0){
for(int i = s.peek() + 1; i < index; i++){
result[i] += (Math.min(height[s.peek()], height[index]) - height[bottom]);
}
}
}
}
return result;
}