Massive Algorithms: LeetCode 391

http://bookshadow.com/weblog/2016/08/28/leetcode-perfect-rectangle/

Given N axis-aligned rectangles where N > 0, determine if they all together form an exact cover of a rectangular region.

Each rectangle is represented as a bottom-left point and a top-right point. For example, a unit square is represented as [1,1,2,2]. (coordinate of bottom-left point is (1, 1) and top-right point is (2, 2)).

Example 1:

rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [3,2,4,4],
  [1,3,2,4],
  [2,3,3,4]
]

Return true. All 5 rectangles together form an exact cover of a rectangular region.

Example 2:

rectangles = [
  [1,1,2,3],
  [1,3,2,4],
  [3,1,4,2],
  [3,2,4,4]
]

Return false. Because there is a gap between the two rectangular regions.

Example 3:

rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [1,3,2,4],
  [3,2,4,4]
]

Return false. Because there is a gap in the top center.

Example 4:

rectangles = [
  [1,1,3,3],
  [3,1,4,2],
  [1,3,2,4],
  [2,2,4,4]
]

Return false. Because two of the rectangles overlap with each other.

X.
http://www.cnblogs.com/grandyang/p/5825619.html

这道题是LeetCode第二周编程比赛的压轴题目，然而我并没有做出来，我想了两种方法都无法通过OJ的大数据集合，第一种方法是对于每一个矩形，我将其拆分为多个面积为1的单位矩形，然后以其左下方的点为标记，用一个哈希表建立每一个单位矩形和遍历到的矩形的映射，因为每个单位矩形只能属于一个矩形，否则就会有重叠，我感觉这种思路应该没错，但是由于把每一个遍历到的矩形拆分为单位矩形再建立映射很费时间，尤其是当矩形很大的时候，TLE就很正常了，后来我试的第二种方法是对于遍历到的每个矩形都和其他所有矩形检测一遍是否重叠，这种方法也是毫无悬念的TLE。

博主能力有限，只能去论坛中找各位大神的解法，发现下面两种方法比较fancy，也比较好理解。首先来看第一种方法，这种方法的设计思路很巧妙，利用了mask，也就是位操作Bit Manipulation的一些技巧，下面这张图来自这个帖子：

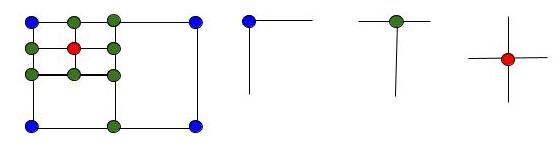
所有的矩形的四个顶点只会有下面蓝，绿，红三种情况，其中蓝表示该顶点周围没有其他矩形，T型的绿点表示两个矩形并排相邻，红点表示四个矩形相邻，那么在一个完美矩形中，蓝色的点只能有四个，这是个很重要的判断条件。我们再来看矩形的四个顶点，我们按照左下，左上，右上，右下的顺序来给顶点标号为1，2，4，8，为啥不是1，2，3，4呢，我们注意它们的二进制1(0001)，2(0010)，4(0100)，8(1000)，这样便于我们与和或的操作，我们还需要知道的一个判定条件是，当一个点是某一个矩形的左下顶点时，这个点就不能是其他矩形的左下顶点了，这个条件对于这四种顶点都要成立，那么对于每一个点，如果它是某个矩形的四个顶点之一，我们记录下来，如果在别的矩形中它又是相同的顶点，那么直接返回false即可，这样就体现了我们标记为1，2，4，8的好处，我们可以按位检查1。如果每个点的属性没有冲突，那么我们来验证每个点的mask是否合理，通过上面的分析，我们知道每个点只能是蓝，绿，红三种情况的一种，其中蓝的情况是mask的四位中只有一个1，分别就是1(0001)，2(0010)，4(0100)，8(1000)，而且蓝点只能有四个；那么对于T型的绿点，mask的四位中有两个1，那么就有六种情况，分别是12(1100), 10(1010), 9(1001), 6(0110), 5(0101), 3(0011)；而对于红点，mask的四位都是1，只有一种情况15(1111)，那么我们可以通过直接找mask是1，2，4，8的个数，也可以间接通过找不是绿点和红点的个数，看是否是四个。最后一个判定条件是每个矩形面积累加和要等于最后的大矩形的面积，那么大矩形的面积我们通过计算最小左下点和最大右上点来计算出来即可，参见代码如下：

https://leetcode.com/problems/perfect-rectangle/discuss/87181/Really-Easy-Understanding-Solution(O(n)-Java)

The right answer must satisfy two conditions:

the large rectangle area should be equal to the sum of small rectangles
count of all the points should be even, and that of all the four corner points should be one

https://discuss.leetcode.com/topic/55997/short-java-solution-with-explanation-updated

If all rectangles can form an exact rectangular area, they should follow these conditions:

The sum of area of all small rectangles should equal to the area of large rectangle.
At any position except outer four corners, the amount of overlapping corners should be even (2, 4).
Corners that overlap at the same point should be different type (top-left, top-right, bottom-left, bottom-right).

So, I used

Four int variables to record the boundaries of large rectangle and then calculate the area.
A hashmap that maps corner with its type.
Four numbers (1, 2, 4, 8) to represent four types of corner. Then use bit manipulation to modify and check.

O(n) time complexity, O(n) space, 112 ms run time.

    Map<String, Integer> map = new HashMap<String, Integer>();
    public boolean isRectangleCover(int[][] rectangles) {
        if (rectangles.length == 0 || rectangles[0].length == 0) return false;
        int lx = Integer.MAX_VALUE, ly = lx, rx = Integer.MIN_VALUE, ry = rx, sum = 0;
        for (int[] rec : rectangles) {
            lx = Math.min(lx, rec[0]);
            ly = Math.min(ly, rec[1]);
            rx = Math.max(rx, rec[2]);
            ry = Math.max(ry, rec[3]);
            sum += (rec[2] - rec[0]) * (rec[3] - rec[1]);
            //bottom-left
            if (overlap(rec[0] + " " + rec[1], 1)) return false;
            //top-left
            if (overlap(rec[0] + " " + rec[3], 2)) return false;
            //bottom-right
            if (overlap(rec[2] + " " + rec[1], 4)) return false;
            //top-right
            if (overlap(rec[2] + " " + rec[3], 8)) return false;
        }
        int count = 0;
        Iterator<Integer> iter = map.values().iterator();
        while (iter.hasNext()) {
            Integer i = iter.next();
            if (i != 15 && i != 12 && i != 10 && i != 9 && i != 6 && i != 5 && i != 3) count++;
        }
        return count == 4 && sum == (rx - lx) * (ry - ly);
    }
    
    private boolean overlap(String corner, Integer type) {
        Integer temp = map.get(corner);
        if (temp == null) temp = type;
        else if ((temp & type) != 0) return true;
        else temp |= type;
        map.put(corner, temp);
        return false;
    }

参考LeetCode Discuss：https://discuss.leetcode.com/topic/55870/share-my-solutions-for-contest-2/2

首先求出所有矩形中横纵坐标的最小/最大值，记为left, right, bottom, top

遍历rectangles，记当前矩形为rect，其左、下、右、上坐标分别为l, b, r, t，则矩形的宽度w = r - l；高度h = t - b

利用数组heights记录矩形左、右边界的高度：

heights[l] += h

heights[r] -= h

利用数组widths记录矩形下、上边界的宽度：

widths[b] += w

widths[t] -= w

从left至right遍历一遍heights数组，检查相邻的height是否相等，并进行累加

从bottom至top遍历一遍widths数组，检查相邻的width是否相等，并进行累加

最后检查上述两个步骤的累加值是否等于(top - bottom) * (right - left)

def isRectangleCover(self, rectangles): """ :type rectangles: List[List[int]] :rtype: bool """ left = min(x[0] for x in rectangles) bottom = min(x[1] for x in rectangles) right = max(x[2] for x in rectangles) top = max(x[3] for x in rectangles) heights = collections.defaultdict(int) widths = collections.defaultdict(int) for rect in rectangles: l, b, r, t = rect h, w = t - b, r - l heights[l] += h heights[r] -= h widths[b] += w widths[t] -= w hSum = heights[left] for x in range(left + 1, right): heights[x] += heights[x - 1] if heights[x] != heights[x - 1]: return False hSum += heights[x] wSum = widths[bottom] for x in range(bottom + 1, top): widths[x] += widths[x - 1] if widths[x] != widths[x - 1]: return False wSum += widths[x] return hSum == wSum == (top - bottom) * (right - left)

https://discuss.leetcode.com/topic/56052/really-easy-understanding-solution-o-n-java

The right answer must satisfy two conditions:

the large rectangle area should be equal to the sum of small rectangles
count of all the points should be even, and that of all the four corner points should be one

For those who are concerned with the validity of the two conditions, here is a quick proof.

Proof to condition 1 is straightforward so I will focus on condition 2. First by observation we know it holds true for a perfect rectangle (consider how many small rectangles can overlap at a particular point: the number has to be even except for the four corner points of the prefect rectangle). The real question is whether it can also be true for some non-perfect rectangle.

Let's begin with the question: what will a non-perfect rectangle look like? Of course it can look like rather complicated but here is a simple way to define it: any non-perfect rectangle can be obtained by a sequence of adding or removing rectangular parts from its perfect counterpart (the order for adding or removing does not matter here). If condition 1 is held true, the non-perfect rectangle must be built by both adding and removing small rectangles such that the total area of added rectangles compensates those of removed.

Without loss of generality, let's focus on the first rectangle (denoted as FR) that is being removed (i.e., we have perfect rectangle before removing it). FR has four corner points. Before removing it, each corner points will appear even times. After it's gone, all the four corner points will appear odd times. To make condition 2 hold true, for each of these four points, we have to either add or remove a rectangle such that each of them will once again appear even times. The key here is that the total number of rectangles added or removed is at least two, since the added or removed rectangles cannot overlap with FR, therefore each added or removed rectangle can contain at most two of the four corner points of FR.

Now we have at least two extra rectangles (either added or removed), with a total of eight corner points. Four of those points coincide with the four corner points of FR. What about the other four points? For each of these points, if it belongs to a rectangle that is being removed, then before removing, it must appear even times and after removing, it will appear odd times. If it belongs to a rectangle that is being added, depending on whether it coincides with any point in the perfect rectangle, its number of appearance will still be odd (appear once if does not coincide with any point, odd if it does since the original number of appearance before adding is even). In either case (adding or removing rectangle), there is no way to keep the number of appearance of all points even, therefore condition 2 cannot be true for non-perfect rectangles.

I think this is a flavor of the Packing Problem which I believe what applications are using (for example) to fit horizontal and vertical photos side by side on your rectangle phone

public boolean isRectangleCover(int[][] rectangles) {

        if (rectangles.length == 0 || rectangles[0].length == 0) return false;

        int x1 = Integer.MAX_VALUE;
        int x2 = Integer.MIN_VALUE;
        int y1 = Integer.MAX_VALUE;
        int y2 = Integer.MIN_VALUE;
        
        HashSet<String> set = new HashSet<String>();
        int area = 0;
        
        for (int[] rect : rectangles) {
            x1 = Math.min(rect[0], x1);
            y1 = Math.min(rect[1], y1);
            x2 = Math.max(rect[2], x2);
            y2 = Math.max(rect[3], y2);
            
            area += (rect[2] - rect[0]) * (rect[3] - rect[1]);
            
            String s1 = rect[0] + " " + rect[1];
            String s2 = rect[0] + " " + rect[3];
            String s3 = rect[2] + " " + rect[3];
            String s4 = rect[2] + " " + rect[1];
            
            if (!set.add(s1)) set.remove(s1);
            if (!set.add(s2)) set.remove(s2);
            if (!set.add(s3)) set.remove(s3);
            if (!set.add(s4)) set.remove(s4);
        }
        
        if (!set.contains(x1 + " " + y1) || !set.contains(x1 + " " + y2) || !set.contains(x2 + " " + y1) || !set.contains(x2 + " " + y2) || set.size() != 4) return false;
        
        return area == (x2-x1) * (y2-y1);
    }

http://blog.csdn.net/mebiuw/article/details/52354018
* 核心思想就是:能够正好围成一个矩形的情况就是: * 有且只有: * - 最左下最左上最右下最右上的四个点只出现过一次,其他肯定是成对出现的(保证完全覆盖) * - 上面四个点围成的面积,正好等于所有子矩形的面积之和(保证不重复)

public boolean isRectangleCover(int[][] rectangles) { int left = Integer.MAX_VALUE; int right = Integer.MIN_VALUE; int top = Integer.MIN_VALUE; int bottom = Integer.MAX_VALUE; int n = rectangles.length; HashSet<String> flags = new HashSet<String>(); int totalArea = 0; for(int i=0;i<n;i++){ left = Math.min(left,rectangles[i][0]); bottom = Math.min(bottom,rectangles[i][1]); right = Math.max(right,rectangles[i][2]); top = Math.max(top,rectangles[i][3]); totalArea += (rectangles[i][3]-rectangles[i][1])*(rectangles[i][2]-rectangles[i][0]); String pointLT = rectangles[i][0] + " "+ rectangles[i][3]; String pointLB = rectangles[i][0] + " "+ rectangles[i][1]; String pointRT = rectangles[i][2] + " "+ rectangles[i][3]; String pointRB = rectangles[i][2] + " "+ rectangles[i][1]; if (!flags.contains(pointLT)) flags.add(pointLT); else flags.remove(pointLT); if (!flags.contains(pointLB)) flags.add(pointLB); else flags.remove(pointLB); if (!flags.contains(pointRT)) flags.add(pointRT); else flags.remove(pointRT); if (!flags.contains(pointRB)) flags.add(pointRB); else flags.remove(pointRB); } if(flags.size()==4 && flags.contains(left+" "+top) && flags.contains(left+" "+bottom) && flags.contains(right+" "+bottom) && flags.contains(right+" "+top)){ return totalArea == (right - left) * (top - bottom); } return false; }

http://www.guoting.org/leetcode/leetcode-391-perfect-rectangle/
http://www.voidcn.com/blog/corpsepiges/article/p-6194803.html

1.我们都知道,一个矩形是由四个顶点组成的,如果让许多个小矩形能够拼接成一个大矩形,那么除了大矩形四个顶点的坐标之外,其它的坐标应该都出现两次,这样才能保证完全覆盖

2.光满足第一点还不可以,比如题目中的Example 4,虽然满足条件一,但是出现了重复,所以需要满足下面的一点:大矩形的面积应该是所有小矩形的面积之和

所以,需要判断题目中给定的坐标能不能满足以上两点,满足的话,就可以构成一个矩形。

    public boolean isRectangleCover(int[][] rectangles) {
        if(rectangles==null||rectangles.length==0) return false;
        int x1=Integer.MAX_VALUE,x2=Integer.MIN_VALUE,y1=Integer.MAX_VALUE,y2=Integer.MIN_VALUE;
        Set<String> set=new HashSet<>();
        int area=0;
        for(int[] rect:rectangles){
            x1=Math.min(x1,rect[0]);
            y1=Math.min(y1,rect[1]);
            x2=Math.max(x2,rect[2]);
            y2=Math.max(y2,rect[3]);

            area+=(rect[2]-rect[0])*(rect[3]-rect[1]);

            String s1=rect[0]+" "+rect[1];
            String s2=rect[0]+" "+rect[3];
            String s3=rect[2]+" "+rect[1];
            String s4=rect[2]+" "+rect[3];

            if(set.contains(s1))
                set.remove(s1);
            else
                set.add(s1);

            if(set.contains(s2))
                set.remove(s2);
            else
                set.add(s2);

            if(set.contains(s3))
                set.remove(s3);
            else
                set.add(s3);

            if(set.contains(s4))
                set.remove(s4);
            else
                set.add(s4);
        }
        if(!set.contains(x1+" "+y1)||!set.contains(x1+" "+y2)||!set.contains(x2+" "+y1)||!set.contains(x2+" "+y2)||set.size()!=4) return false;
        return area==(x2-x1)*(y2-y1);
    }

Best: https://discuss.leetcode.com/topic/55923/o-n-solution-by-counting-corners-with-detailed-explaination

The following code passes through not only the OJ but also various test cases others have pointed out.

Idea

Consider how the corners of all rectangles appear in the large rectangle if there's a perfect rectangular cover.
Rule 1: The local shape of the corner has to follow one of the three following patterns

Corner of the large rectangle (blue): it occurs only once among all rectangles
T-junctions (green): it occurs twice among all rectangles
Cross (red): it occurs four times among all rectangles

Rule 2: A point can only be the top-left corner of at most one sub-rectangle. Similarly it can be the top-right/bottom-left/bottom-right corner of at most one sub-rectangle. Otherwise overlaps occur.

Proof of correctness

Obviously, any perfect cover satisfies the above rules. So the main question is whether there exists an input which satisfy the above rules, yet does not compose a rectangle.

First, any overlap is not allowed based on the above rules because

aligned overlap like [[0, 0, 1, 1], [0, 0, 2, 2]] are rejected by Rule 2.
unaligned overlap will generate a corner in the interior of another sub-rectangle, so it will be rejected by Rule 1.

Second, consider the shape of boundary for the combined shape. The cross pattern does not create boundary. The corner pattern generates a straight angle on the boundary, and the T-junction generates a straight border.
So the shape of the union of rectangles has to be rectangle(s).

Finally, if there are more than two non-overlapping rectangles, at least 8 corners will be found, and cannot be matched to the 4 bounding box corners (be reminded we have shown that there is no chance of overlapping).
So the cover has to be a single rectangle if all above rules are satisfied.

Algorithm

Step1: Based on the above idea we maintain a mapping from (x, y)->mask by scanning the sub-rectangles from beginning to end.
- (x, y) corresponds to corners of sub-rectangles
- mask is a 4-bit binary mask. Each bit indicates whether there have been a sub-rectangle with a top-left/top-right/bottom-left/bottom-right corner at (x, y). If we see a conflict while updating mask, it suffice to return a false during the scan.
- In the meantime we obtain the bounding box of all rectangles (which potentially be the rectangle cover) by getting the upper/lower bound of x/y values.
Step 2: Once the scan is done, we can just browse through the unordered_map to check the whether the mask corresponds to a T junction / cross, or corner if it is indeed a bounding box corner.
(note: my earlier implementation uses counts of bits in mask to justify corners, and this would not work with certain cases as @StefanPochmann points out).

Complexity

The scan in step 1 is O(n) because it loop through rectangles and inside the loop it updates bounding box and unordered_map in O(1) time.

Step2 visits 1 corner at a time with O(1) computations for at most 4n corners (actually much less because either corner overlap or early stopping occurs). So it's also O(n).

    public boolean isRectangleCover(int[][] rectangles) {
        int left = Integer.MAX_VALUE, down = Integer.MAX_VALUE;
        int right = Integer.MIN_VALUE, up = Integer.MIN_VALUE;
        
        Map<Integer, HashMap<Integer, Integer>> map = new HashMap<>();
        for (int i = 0; i < rectangles.length; i++) {
            left = Math.min(left, rectangles[i][0]);
            down = Math.min(down, rectangles[i][1]); 
            right = Math.max(right, rectangles[i][2]);
            up = Math.max(up, rectangles[i][3]);
            if (!helper(map, rectangles[i][0], rectangles[i][1], 1)) return false;
            if (!helper(map, rectangles[i][2], rectangles[i][1], 2)) return false;
            if (!helper(map, rectangles[i][2], rectangles[i][3], 4)) return false;
            if (!helper(map, rectangles[i][0], rectangles[i][3], 8)) return false;
        }
        
        for (Integer x : map.keySet()) {
            for (Integer y : map.get(x).keySet()) {
                Integer v = map.get(x).get(y);
                if ((x == left || x == right) && (y == up || y == down)) {
                    if (v != 1 && v != 2 && v != 4 && v != 8) return false;
                } else {
                    if (v != 3 && v != 6 && v != 9 && v != 12 && v != 15) return false;
                }
            }
        }
        
        return true;
    }
    private boolean helper(Map<Integer, HashMap<Integer, Integer>> map, int x, int y, int pos) {
        if (!map.containsKey(x)) map.put(x, new HashMap<>());
        if (!map.get(x).containsKey(y)) map.get(x).put(y, 0);
        if ((map.get(x).get(y) & pos) != 0) return false;
        map.get(x).put(y, map.get(x).get(y) | pos);
        
        return true;
    }

http://www.cnblogs.com/dongling/p/5831106.html

刚开始想到的一个方法是先遍历所有的矩形，找出最小的(leftMost,bottomMost)和最大的(rightMost,topMost),这是所有矩形所可能覆盖的最大的区域。然后定义一个二维数组：

int[][] area = new int[topMost-bottomMost][rightMost-leftMost],

再遍历一次所有的矩形，对矩形 rect,做如下判断：

int totalArea=0;
for(int[] rect:rectangles){
    for(int i=rect[1]-bottomMost;i<rect[3]-bottomMost;i++){
        for(int j=rect[0]-leftMost;j<rect[2]-leftMost;j++){
            totalArea++;
            if(area[i][j]>=1){//说明出现了重叠覆盖区域
                return false;
            }
            else{
                area[i][j]++;
            }
    } 
}

当遍历完所有矩形后，首先判断

if(totalArea!=(rightMost-leftMost)*(topMost-bottomMost)){
    return false;
}

因为如果要实现完全覆盖，必须有 totalArea=(rightMost-leftMost)*(topMost-bottomMost).

满足了相等条件后,再判断是否area[][]数组中所有的数据均为1----是，则说明最大覆盖区域中的每个小单元均被覆盖了一次，满足条件，返回 true；否，则说明有的区域没有覆盖到，返回 false。

上述算法的思想是正确的，但是当输入数据量覆盖面积较大时，会出现 Memory Exceeded 的错误。考虑使用一个 bit 来表示一个单元面积，结果出现了 Time Limit Exceeded 的错误。

最终考虑使用如下算法思想：

任意一个矩形均有4个顶点，当出现Perfect Rectangle时，在最大覆盖矩形内部，所有其它矩形的任意一个顶点均会出现偶数次（因为一个矩形旁边应当有一个或三个矩形和它紧密相连，那么这个相接的顶点就出现了偶数次）。所以，可以构建一个HashSet set,以一个矩形的四个顶点的(x,y)坐标构造字符串 (x+","+y),以该字符串做键值，当set中不存在该键值时，则存入该键值；当set中存在该键值时，则删除该键值；最终set中应该只剩下四个键，这四个键即是最大覆盖矩形的四个顶点。

Java 算法实现如下(并不正确)：

public class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        if(rectangles.length==0||rectangles[0].length==0){
            return false;
        }
        else{
            HashSet<String>set=new HashSet<>();
            int leftMost=Integer.MAX_VALUE;
            int bottomMost=Integer.MAX_VALUE;
            int rightMost=Integer.MIN_VALUE;
            int topMost=Integer.MIN_VALUE;
            int x1,y1,x2,y2;
            for(int[] rect:rectangles){
                x1=rect[0];
                y1=rect[1];
                x2=rect[2];
                y2=rect[3];
                //记录最靠边界的点的坐标
                if(x1<leftMost){
                    leftMost=x1;
                }
                if(y1<bottomMost){
                    bottomMost=y1;
                }
                if(x2>rightMost){
                    rightMost=x2;
                }
                if(y2>topMost){
                    topMost=y2;
                }
                //由当前考察的矩形的四个顶点的坐标构成的键值
                String key1=x1+","+y1;
                String key2=x1+","+y2;
                String key3=x2+","+y1;
                String key4=x2+","+y2;
                //删除那些出现了偶数次的键值
                if(set.contains(key1)){
                    set.remove(key1);
                }
                else{
                    set.add(key1);
                }
                
                if(set.contains(key2)){
                    set.remove(key2);
                }
                else{
                    set.add(key2);
                }
                
                if(set.contains(key3)){
                    set.remove(key3);
                }
                else{
                    set.add(key3);
                }
                
                if(set.contains(key4)){
                    set.remove(key4);
                }
                else{
                    set.add(key4);
                }
            }
            String key1=leftMost+","+bottomMost;
            String key2=leftMost+","+topMost;
            String key3=rightMost+","+bottomMost;
            String key4=rightMost+","+topMost;
            if(set.size()!=4||!set.contains(key1)||
                    !set.contains(key2)||!set.contains(key3)||
                    !set.contains(key4)){
                return false;
            }
            else{
                return true;
            }
        }
    }
}

结果出现如下错误：

如上数据所示，[0,0,3,3] 为最大覆盖矩形，两个[1,1,2,2]又都在其内部，且互相抵消掉了，所以该输入数据成功地避开了所有的检测，返回了不正确的答案 true。改正方法是添加一个 long area 数据用以记录所有矩形的总面积，检测 area 是否和 (rightMost-leftMost)*(topMost-bottomMost)相等，若不等，则说明没有完全覆盖或者出现了重叠覆盖，返回 false；若相等，则做进一步判断。新代码如下：

Java算法实现：

public class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        if(rectangles.length==0||rectangles[0].length==0){
            return false;
        }
        else{
            HashSet<String>set=new HashSet<>();
            int leftMost=Integer.MAX_VALUE;
            int bottomMost=Integer.MAX_VALUE;
            int rightMost=Integer.MIN_VALUE;
            int topMost=Integer.MIN_VALUE;
            int x1,y1,x2,y2;
            long area=0;
            for(int[] rect:rectangles){
                x1=rect[0];
                y1=rect[1];
                x2=rect[2];
                y2=rect[3];
                area+=(x2-x1)*(y2-y1);//累积记录已遍历的矩形的面积
                //记录最靠边界的点的坐标
                if(x1<leftMost){
                    leftMost=x1;
                }
                if(y1<bottomMost){
                    bottomMost=y1;
                }
                if(x2>rightMost){
                    rightMost=x2;
                }
                if(y2>topMost){
                    topMost=y2;
                }
                if(area>(rightMost-leftMost)*(topMost-bottomMost)){
                    //目前遍历的矩形的面积已经大于了所能覆盖的面积，则一定存在了重叠
                    return false;
                }
                //由当前考察的矩形的四个顶点的坐标构成的键值
                String key1=x1+","+y1;
                String key2=x1+","+y2;
                String key3=x2+","+y1;
                String key4=x2+","+y2;
                //totalCouverCount用以记录是否出现了某个矩形完全覆盖了之前的某个矩形
                //删除那些出现了偶数次的键值
                if(set.contains(key1)){
                    set.remove(key1);
                }
                else{
                    set.add(key1);
                }
                
                if(set.contains(key2)){
                    set.remove(key2);
                }
                else{
                    set.add(key2);
                }
                
                if(set.contains(key3)){
                    set.remove(key3);
                }
                else{
                    set.add(key3);
                }
                
                if(set.contains(key4)){
                    set.remove(key4);
                }
                else{
                    set.add(key4);
                }
            }
            
            if(area!=(rightMost-leftMost)*(topMost-bottomMost)){//说明没有完全覆盖或出现了重叠覆盖
                return false;
            }
            
            String key1=leftMost+","+bottomMost;
            String key2=leftMost+","+topMost;
            String key3=rightMost+","+bottomMost;
            String key4=rightMost+","+topMost;
            if(set.size()!=4||!set.contains(key1)||
                    !set.contains(key2)||!set.contains(key3)||
                    !set.contains(key4)){
                return false;
            }
            else{
                return true;
            }
        }
    }
}

https://discuss.leetcode.com/topic/55944/o-n-log-n-sweep-line-solution

Standard sweep line solution.
Basic idea:
Sort by x-coordinate.
Insert y-interval into TreeSet, and check if there are intersections.
Delete y-interval.



this way first to sort x-coordinate in order to handle rectangle from left to right
when the time is same then sort by the rect[0], why do like this?

this situation happens in like top-right in 4th and bottom-left in 5th point in the below picture.


Because we want to handle rectangle from left to right and every handle process there is only one rectangle in the vertical range, when handle 5th rectangle 4th rect should be removed, handle 2th rect 1th rect should be removed. So we need sort by rect[0] when time is same.

After the traversal sequence is set by PriorityQueue, we use the treeSet to judge two rect is intersections or not, and we can see every handle process, the yRange should equal the high of the largest rectangle outside if it is true.





For example, so basically we have three rects: Rect 1 (1, 1, 3, 3); Rect2 (1, 3, 3, 4); and Rect3 (2, 3, 3, 4). Rect3 intersects with Rect2 obviously.

So what the tree set does is that, when the sweep line goes to the time 2 (x = 2), the tree set still contains Rect2(1, 3, 3, 4) because the right time event (time=3) has not been polled from the priority queue. which means the shaded area is kind of like a horizontal blocking space (x >= 2, 3 <= y <= 4) whenever the new rect is not on the shaded area's bottom left or top right, there is an intersection.

And the set.add() will return false when the compare func returns 0.


public class Event implements Comparable<Event> {
 int time;
 int[] rect;

 public Event(int time, int[] rect) {
  this.time = time;
  this.rect = rect;
 }
 
 public int compareTo(Event that) {
  if (this.time != that.time) return this.time - that.time;
  else return this.rect[0] - that.rect[0];
 }
}

public boolean isRectangleCover(int[][] rectangles) {
 PriorityQueue<Event> pq = new PriorityQueue<Event> ();
        // border of y-intervals
 int[] border= {Integer.MAX_VALUE, Integer.MIN_VALUE};
 for (int[] rect : rectangles) {
  Event e1 = new Event(rect[0], rect);
  Event e2 = new Event(rect[2], rect);
  pq.add(e1);
  pq.add(e2);
  if (rect[1] < border[0]) border[0] = rect[1];
  if (rect[3] > border[1]) border[1] = rect[3];
 }
 TreeSet<int[]> set = new TreeSet<int[]> (new Comparator<int[]> () {
  @Override
                // if two y-intervals intersects, return 0
  public int compare (int[] rect1, int[] rect2) {
   if (rect1[3] <= rect2[1]) return -1;
   else if (rect2[3] <= rect1[1]) return 1;
   else return 0;
  }
 });
 int yRange = 0;
 while (!pq.isEmpty()) {
  int time = pq.peek().time;
  while (!pq.isEmpty() && pq.peek().time == time) {
   Event e = pq.poll();
   int[] rect = e.rect;
   if (time == rect[2]) {
    set.remove(rect);
    yRange -= rect[3] - rect[1];
   } else {
    if (!set.add(rect)) return false;
    yRange += rect[3] - rect[1];
   }
  }
                // check intervals' range
  if (!pq.isEmpty() && yRange != border[1] - border[0]) {
                        return false;
   //if (set.isEmpty()) return false;
   //if (yRange != border[1] - border[0]) return false;
  }
 }
 return true;
}
https://segmentfault.com/a/1190000006739199

== Wrong answer, doesn't work
ERROR: [[0,0,1,1],[0,1,3,2],[1,0,2,2]] expected false but return true

    public boolean isRectangleCover(int[][] A) {
        int m = A.length;
        int minlbrow = Integer.MAX_VALUE, minlbcol = Integer.MAX_VALUE, maxrurow = 0, maxrucol = 0;
        for (int i = 0; i < m; i++) {
            minlbrow = Math.min(minlbrow, A[i][1]);
            minlbcol = Math.min(minlbcol, A[i][0]);
            maxrurow = Math.max(maxrurow, A[i][3]);
            maxrucol = Math.max(maxrucol, A[i][2]);
        }
        int[] largest = {minlbrow, minlbcol, maxrurow, maxrucol};
        int alarge = area(largest);
        int asum = 0;
        for (int i = 0; i < m; i++) {
            asum += area(A[i]);
        }
        return asum == alarge;
    }
    public int area(int[] a) {
        if (a.length != 4) return 0;
        return (a[2]-a[0]) * (a[3]-a[1]);
    }

LeetCode 391 - Perfect Rectangle

Idea

Proof of correctness

Algorithm

Complexity

Labels

Popular Posts