https://leetcode.com/problems/matchsticks-to-square/
https://leetcode.com/articles/matchsticks-to-square/
X.
https://leetcode.com/problems/matchsticks-to-square/discuss/95729/Java-DFS-Solution-with-Explanation
Sorting the input array
This is a NP problem. Time complexity should be O(4 ^ n), n is the length of array.
First Optimization:
In the recurrence relation above, we concluded that if
Sorting the input array
https://leetcode.com/problems/matchsticks-to-square/discuss/95746/C%2B%2B-bit-masking-%2B-DP-solution-with-detailed-comments
The bitmasking technique may look sophisticated but the idea is actually pretty straightforward because it uses brute force with some optimizations. A bitmask is used as a representation of a subset. For example if nums = {1,1,2,2,2}, then a bitmask = 01100 represents the subset {1,2}.
https://discuss.leetcode.com/topic/72125/java-dfs-dp-solution
http://www.cnblogs.com/grandyang/p/6238425.html
其实这题还有迭代的方法,很巧妙的利用到了位操作的特性,前面的基本求和跟判断还是一样,然后建立一个变量all,初始化为(1 << n) - 1,这是什么意思呢,all其实是一个mask,数组中有多少个数字,all就有多少个1,表示全选所有的数字,然后变量target表示一条边的长度。我们建立两个一位向量masks和validHalf,其中masks保存和target相等的几个数字位置的mask,validHalf保存某个mask是否是总和的一半。然后我们从0遍历到all,实际上就是遍历所有子数组,然后我们根据mask来计算出子数组的和,注意这里用了15,而不是32,因为题目中说了数组元素个数不会超过15个。我们算出的子数组之和如果等于一条边的长度target,我们遍历masks数组中其他等于target的子数组,如果两个mask相与不为0,说明有公用的数字,直接跳过;否则将两个mask或起来,说明我们当前选的数字之和为数组总和的一半,更新validHalf的对应位置,然后我们通过all取出所有剩下的数组,并在validHalf里查找,如果也为true,说明我们成功的找到了四条边
def makesquare(self, nums): """ :type nums: List[int] :rtype: bool """ if sum(nums) % 4: return False self.q = sum(nums) / 4 self.dp = collections.defaultdict(lambda: collections.defaultdict()) return self.solve(nums, 4) def solve(self, nums, part): total = sum(nums) if part == 1: return total == self.q size = len(nums) if size < part or total % part: return False tnums = tuple(nums) if part in self.dp[tnums]: return self.dp[tnums][part] for x in range(1, (1 << size) - 1): left, right = [], [] for y in range(size): if x & (1 << y): left.append(nums[y]) else: right.append(nums[y]) if sum(left) != self.q: continue if self.solve(right, part - 1): self.dp[tnums][part] = True return True self.dp[tnums][part] = False return False
X.
https://discuss.leetcode.com/topic/72103/simple-recursion-java-solution-66ms
http://blog.jerkybible.com/2016/12/30/LeetCode-473-Matchsticks-to-Square/
X. DP
https://leetcode.com/articles/matchsticks-to-square/
Remember the story of Little Match Girl? By now, you know exactly what matchsticks the little match girl has, please find out a way you can make one square by using up all those matchsticks. You should not break any stick, but you can link them up, and each matchstick must be used exactly one time.
Your input will be several matchsticks the girl has, represented with their stick length. Your output will either be true or false, to represent whether you can save this little girl or not.
Example 1:
Example 2:
Note:
- The length sum of the given matchsticks is in the range of
0to10^9. - The length of the given matchstick array will not exceed
15.
https://leetcode.com/articles/matchsticks-to-square/
This problem boils down to splitting an array of integers into subsets where all of these subsets are:mutually exclusive i.e. no specific element of the array is shared by any two of these subsets, and have the same sum which is equal to the side of our square.
We know that we will have different subsets. The sum of elements of these subsets would be . If the sum if not divisible by , that implies that subsets of equal value are not possible and we don't need to do any further processing on this.
The only question that remains now for us to solve is:
what subset a particular element belongs to?
If we are able to figure that out, then there's nothing else left to do. But, since we can't say which of the subsets would contain a particular element, we try out all the options.
X. DFS
It is possible that a matchstick can be a part of any of the 4 sides of the resulting square, but which one of these choices leads to an actual square is something we don't know.
This means that for every matchstick in our given array, we have different options each representing the side of the square or subset that this matchstick can be a part of.
We try out all of them and keep on doing this recursively until we exhaust all of the possibilities or until we find an arrangement of our matchsticks such that they form the square.
Algorithm
- As discussed previously, we will follow a recursive, depth first approach to solve this problem. So, we have a function that takes the current matchstick index we are to process and also the number of sides of the square that are completely formed till now.
- If all of the matchsticks have been used up and 4 sides have been completely formed, that implies our square is completely formed. This is the base case for the recursion.
- For the current matchstick we have 4 different options. This matchstick at can be a part of any of the sides of the square. We try out the 4 options by recursing on them.
- If any of these recursive calls returns , then we return from there, else we return
This solution is very slow as is. However, we can speed it up considerably by a small trick and that is to
sort our matchsticks sizes in reverse order before processing them recursively.
The reason for this is that if there is no solution, trying a longer matchstick first will get to negative conclusion earlier.
e.g. . In this case we can have a square of size 5 but the largest side 8 doesn't fit in anywhere i.e. cannot be a part of any of the sides (because we can't break matchsticks according to the question) and hence we can simply return without even considering the remaining matchsticks.
Complexity Analysis
- Time Complexity : because we have a total of sticks and for each one of those matchsticks, we have different possibilities for the subsets they might belong to or the side of the square they might be a part of.
public List<Integer> nums;
public int[] sums;
public int possibleSquareSide;
public Solution() {
this.sums = new int[4];
}
// Depth First Search function.
public boolean dfs(int index) {
// If we have exhausted all our matchsticks, check if all sides of the square
// are of equal length
if (index == this.nums.size()) {
return sums[0] == sums[1] && sums[1] == sums[2] && sums[2] == sums[3];
}
// Get current matchstick.
int element = this.nums.get(index);
// Try adding it to each of the 4 sides (if possible)
for (int i = 0; i < 4; i++) {
if (this.sums[i] + element <= this.possibleSquareSide) {
this.sums[i] += element;
if (this.dfs(index + 1)) {
return true;
}
this.sums[i] -= element;
}
}
return false;
}
public boolean makesquare(int[] nums) {
// Empty matchsticks.
if (nums == null || nums.length == 0) {
return false;
}
// Find the perimeter of the square (if at all possible)
int L = nums.length;
int perimeter = 0;
for (int i = 0; i < L; i++) {
perimeter += nums[i];
}
this.possibleSquareSide = perimeter / 4;
if (this.possibleSquareSide * 4 != perimeter) {
return false;
}
// Convert the array of primitive int to ArrayList (for sorting).
this.nums = Arrays.stream(nums).boxed().collect(Collectors.toList());
Collections.sort(this.nums, Collections.reverseOrder());
return this.dfs(0);
}
https://leetcode.com/problems/matchsticks-to-square/discuss/95752/Java-DFS-solution-with-various-optimizations-(sorting-sequential-partition-DP)
For better description of the problem, let's reformulate it in the following symbolic way:
Given an array
nums with n elements, let T(i, s1, s2, s3, s4) denote whether we can partition the subarray nums[0, i](both inclusive) into four disjoint groups such that the sum of elements in the j-th group is sj, with j = 1, 2, 3, 4.
With this definition, our original problem will be
T(n - 1, side, side, side, side) where side is the side length of the square.
To solve for
T(i, s1, s2, s3, s4), note that the last element of the subarray nums[0, i] (which is nums[i]) must belong to one of the disjoint groups, therefore we have the following recurrence relation:T(i, s1, s2, s3, s4) = T(i - 1, s1 - nums[i], s2, s3, s4) ||
T(i - 1, s1, s2 - nums[i], s3, s4) ||
T(i - 1, s1, s2, s3 - nums[i], s4) ||
T(i - 1, s1, s2, s3, s4 - nums[i])
The interpretation is as follows: if
nums[i] belongs to the j-th group, we subtract it from sj, then recursively solve for the subproblem with reduced array size and modified group sum. However, we do not know which group it belongs to beforehand, therefore each of the groups will be examined until we either hit the right group or determine that no partition is possible. Also note that if all elements in the input array are positive, an element cannot fall into a group with a group sum smaller than the element itself, i.e., nums[i] cannot belong to the j-th group if nums[i] > sj.
The termination condition for the recursion is when the subarray is empty, i.e.,
https://discuss.leetcode.com/topic/72107/java-dfs-solution-with-explanationi = -1, at which time we will check whether the sum of each group is zero. If so, a partition is found and return true; otherwise no partition is possible and return false.
According to https://en.wikipedia.org/wiki/Partition_problem, the partition problem (or number partitioning) is the task of deciding whether a given multiset
S of positive integers can be partitioned into two subsets S1 and S2 such that the sum of the numbers in S1 equals the sum of the numbers in S2. The partition problem is NP-complete.
When I trying to think how to apply dynamic programming solution of above problem to this one (difference is divid
The length sum of the given matchsticks is in the range of
The length of the given matchstick array will not exceed
S into 4 subsets), I took another look at the constraints of the problem:The length sum of the given matchsticks is in the range of
0 to 10^9.The length of the given matchstick array will not exceed
15.
Sounds like the input will not be very large... Then why not just do DFS? In fact, DFS solution passed judges.
public boolean makesquare(int[] nums) {
if (nums == null || nums.length < 4) return false;
int sum = 0;
for (int num : nums) sum += num;
if (sum % 4 != 0) return false;
return dfs(nums, new int[4], 0, sum / 4);
}
private boolean dfs(int[] nums, int[] sums, int index, int target) {
if (index == nums.length) {
if (sums[0] == target && sums[1] == target && sums[2] == target) {
return true;
}
return false;
}
for (int i = 0; i < 4; i++) {
if (sums[i] + nums[index] > target) continue;
sums[i] += nums[index];
if (dfs(nums, sums, index + 1, target)) return true;
sums[i] -= nums[index];
}
return false;
}https://leetcode.com/problems/matchsticks-to-square/discuss/95729/Java-DFS-Solution-with-Explanation
Sorting the input array
DESC will make the DFS process run much faster. Reason behind this is we always try to put the next matchstick in the first subset. If there is no solution, trying a longer matchstick first will get to negative conclusion earlier. Following is the updated code. Runtime is improved from more than 1000ms to around 40ms. A big improvement public boolean makesquare(int[] nums) {
if (nums == null || nums.length < 4) return false;
int sum = 0;
for (int num : nums) sum += num;
if (sum % 4 != 0) return false;
Arrays.sort(nums);
reverse(nums);
return dfs(nums, new int[4], 0, sum / 4);
}
private boolean dfs(int[] nums, int[] sums, int index, int target) {
if (index == nums.length) {
if (sums[0] == target && sums[1] == target && sums[2] == target) {
return true;
}
return false;
}
for (int i = 0; i < 4; i++) {
if (sums[i] + nums[index] > target) continue;
sums[i] += nums[index];
if (dfs(nums, sums, index + 1, target)) return true;
sums[i] -= nums[index];
}
return false;
}This is a NP problem. Time complexity should be O(4 ^ n), n is the length of array.
First Optimization:
each matchstick must be used exactly one time.
The description says we need to use every single match exactly once, so we can get the length of each side of the square if there is one.
if the current length is larger than target length, we don't need to go any further.
if the current length is larger than target length, we don't need to go any further.
if (sidesLength[i] + matches[index] > target) continue; by adding this line of code into dfs function, solution get TLE at 147th test case.Second Optimization:
After reading the description again, I realize that the length of a single match can be very long. If they put long ones after short ones, it will take a long time before my algorithm return false.
So I sort all the matches to avoid the worst case:
So I sort all the matches to avoid the worst case:
sort(nums.begin(), nums.end(), [](const int &l, const int &r){return l > r;});. After putting this line before my algorithm, solution passed all cases and beats 50% solutions. I saw someone's algorithm is amazingly fast, they even make me reconsider wether the problem is NP or not.Third Optimization:
Because their solutions is so fast, I need think about if I can use DP to solve the problem. It turns out that it's still a NP problem, which makes happy again. But I can actually use the concept of DP in optimization: if I have checked the same length before, why do I need to bother checking again?
Although we only have 4 sides in a square, we can still check if we have encountered the same length with the current match. After I add this to my code:
Although we only have 4 sides in a square, we can still check if we have encountered the same length with the current match. After I add this to my code:
int j = i;
while (--j >= 0)
if (sidesLength[i] == sidesLength[j])
break;
if (j != -1) continue; bool dfs(vector<int> &sidesLength,const vector<int> &matches, int index, const int target) {
if (index == matches.size())
return sidesLength[0] == sidesLength[1] && sidesLength[1] == sidesLength[2] && sidesLength[2] == sidesLength[3];
for (int i = 0; i < 4; ++i) {
if (sidesLength[i] + matches[index] > target) // first
continue;
int j = i;
while (--j >= 0) // third
if (sidesLength[i] == sidesLength[j])
break;
if (j != -1) continue;
sidesLength[i] += matches[index];
if (dfs(sidesLength, matches, index + 1, target))
return true;
sidesLength[i] -= matches[index];
}
return false;
}
bool makesquare(vector<int>& nums) {
if (nums.size() < 4) return false;
int sum = 0;
for (const int val: nums) {
sum += val;
}
if (sum % 4 != 0) return false;
sort(nums.begin(), nums.end(), [](const int &l, const int &r){return l > r;}); // second
vector<int> sidesLength(4, 0);
return dfs(sidesLength, nums, 0, sum / 4);
} bool makesquare(vector<int>& nums) {
if(nums.size() < 4) return false;
int sum=0;
for(auto a:nums)
sum+=a;
//If each side is not integer
if(sum%4 != 0) return false;
int side = sum/4;
//Optimize :Reverse sort so that bigger numbers get rejected early on in the expansion tree
sort(nums.begin(),nums.end(), greater<int>() );
//Optimize: If any match is bigger than the expected side
for(auto a:nums)
if(a>side) return false;
vector<int> sides(4,0);
return dfs(nums,sides,0,side);
}
bool dfs(vector<int>& match,vector<int>& sides,int index,int side){
if(index==match.size())
return allSidesEqual(sides);
for(int i=0;i<4;i++)
{
//Optimize 1:
if(sides[i]+match[index]>side)
continue;
//Optimize 2:
if(seenBefore(sides,i))
continue;
sides[i]+=match[index];
if(dfs(match,sides,index+1,side)) return true;
sides[i]-=match[index];
}
return false;
}
inline bool allSidesEqual(const vector<int>& sides){
return sides[0]==sides[1] && sides[1]==sides[2] && sides[2]==sides[3];
}
inline bool seenBefore(const vector<int>& sides,int i){
return i==0 ? false:
i==1 ? sides[1]==sides[0] :
i==2 ? sides[2]==sides[1] || sides[2]==sides[0] :
i==3 ? sides[3]==sides[2] || sides[3]==sides[1] || sides[3]==sides[0] : false;
}
vector<int> nums2; //过滤后的数字,都是小于side的
int len2; // nums的长度
int side; // 边长
int cnt; // 还差 cnt个side长, len2必须大于等于cnt
// 最终需要使得,sums[0] sums[1] ... sums[cnt-1]的值都为side,并且把nums2[]里面的数都使用到
bool dfs(vector<int> &sums, int index)
{
if(index > len2)
return false;
if(index == len2) // index == len2说明所有的数都用完了,那么需要判断了
{
bool flag = true;
for(int i=0;i<cnt;i++)
{
if(sums[i] != side)
{
flag = false;
break;
}
}
return flag;
}
// 对于nums2[index],可以往sums[0],sums[1] ... sums[cnt]中的任何一个塞,需要判重
for(int i=0;i<cnt;i++)
{
if(nums2[index] + sums[i] <= side) //控制sums[i] <= side
{
// 这里必须判断当 两个sum相同时,nums2[index]放入一个就行了,因为放入另外一个跟前一个的搜索是一样的
// 这样会造成重复的搜索,从而超时
// 这个是常用的剪枝操作
if(i > 0 && sums[i] == sums[i-1])
continue;
sums[i] += nums2[index];
// dfs
if(dfs(sums,index + 1))
return true;
sums[i] -= nums2[index]; //回溯
}
}
return false;
}
bool makesquare(vector<int>& nums) {
int len = nums.size();
if(len < 4)
return false;
int he = 0;
for(int i=0;i<len;i++)
he += nums[i];
if(he % 4 != 0)
return false;
side = he / 4; // 边长
// 过滤并判断
nums2.clear();
cnt = 4;
for(int i=0;i<len;i++)
{
if(nums[i] > side)
{
return false;
}else if(nums[i] == side)
{
cnt --;
}else{
nums2.push_back(nums[i]);
}
}
len2 = nums2.size();
if(cnt == 0 && len2 == 0)
return true;
if(cnt == 0 && len2 > 0)
return false;
if(len2 < cnt)
return false;
// 问题转换
if(len2 > 1)
sort(nums2.begin(), nums2.end());
vector<int> sums(cnt,0);
// 可以使用 1,1,2,2,3,3,4的数据 对dfs就行debug观察每一步的操作
return dfs(sums, 0);
//return false;
}
http://code.bitjoy.net/2017/06/10/leetcode-matchsticks-to-square/
第(1)个剪枝策略的含义是先对所有火柴棒的长度从大到小排序,为什么从大到小排序呢,因为我们的dfs过程中的for循环总是首先尝试把每根火柴棒放到第一个组份中,如果本身无解,则从小到大的策略会慢慢累积和,直到最后加上很长的火柴棒才会发现不满足if语句无解;而如果从大到小排序的话,一开始的累加和就很大,如果无解,则很快能发现不满足if。
第(2)个剪枝策略的含义是只有当把这根火柴棒加到这个组份中不会超过预定的edge,才把它加入,然后递归。这个很显然的。
第(3)个剪枝策略参考讨论区,如果递归的时候发现某一个组份当前的和等于之前某个组份的和,因为之前那个组份已经递归过了,所以本质上这次递归会和上次递归一样,可以continue掉。
In the recurrence relation above, we concluded that if
nums[i] > sj, it cannot belong to the j-th group, which implies we needn't even bother to try that case. This condition is most likely to be met if we always choose the maximum element that is currently available in the subarray. Also note that the order of elements does not matter in the partition of the array. Therefore we can sort the input array in ascending order before rushing into DFS. Sorting the input array
DESC will make the DFS process run much faster. Reason behind this is we always try to put the next matchstick in the first subset. If there is no solution, trying a longer matchstick first will get to negative conclusion earlier. Following is the updated code. Runtime is improved from more than 1000ms to around 40ms. A big improvement. public boolean makesquare(int[] nums) {
if (nums == null || nums.length < 4) return false;
int sum = 0;
for (int num : nums) sum += num;
if (sum % 4 != 0) return false;
Arrays.sort(nums);
reverse(nums);
return dfs(nums, new int[4], 0, sum / 4);
}
private boolean dfs(int[] nums, int[] sums, int index, int target) {
if (index == nums.length) {
if (sums[0] == target && sums[1] == target && sums[2] == target) {
return true;
}
return false;
}
for (int i = 0; i < 4; i++) {
if (sums[i] + nums[index] > target) continue;
sums[i] += nums[index];
if (dfs(nums, sums, index + 1, target)) return true;
sums[i] -= nums[index];
}
return false;
}
private void reverse(int[] nums) {
int i = 0, j = nums.length - 1;
while (i < j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
i++; j--;
}
}https://leetcode.com/problems/matchsticks-to-square/discuss/95746/C%2B%2B-bit-masking-%2B-DP-solution-with-detailed-comments
The bitmasking technique may look sophisticated but the idea is actually pretty straightforward because it uses brute force with some optimizations. A bitmask is used as a representation of a subset. For example if nums = {1,1,2,2,2}, then a bitmask = 01100 represents the subset {1,2}.
Time and space complexity look a bit prohibitive though, especially these 3 lines -
vector<bool> validHalfSubsets(1<<n, false);
...
for (int mask = 0; mask <= all; mask++)
...
for (int usedMask : usedMasks)
bool makesquare(vector<int>& nums) {
int n = nums.size();
long sum = accumulate(nums.begin(), nums.end(), 0l);
if (sum % 4)
return false;
long sideLen = sum / 4;
// need to solve the problem of partitioning nums into four equal subsets each having
// sum equal to sideLen
vector<int> usedMasks;
// validHalfSubsets[i] == true iff the subset represented by bitmask i
// has sum == 2*sideLen, AND the subset represented by i can be further partitioned into
// two equal subsets. See below for how it is used.
vector<bool> validHalfSubsets(1<<n, false);
// E.g., if n = 5, (1 << 5 - 1) = 11111 represents the whole set
int all = (1 << n) - 1;
// go through all possible subsets each represented by a bitmask
for (int mask = 0; mask <= all; mask++) {
long subsetSum = 0;
// calculate the sum of this subset
for (int i = 0; i < 32; i++) {
if ((mask >> i) & 1)
subsetSum += nums[i];
}
// if this subset has what we want
if (subsetSum == sideLen) {
for (int usedMask : usedMasks) {
// if this mask and usedMask are mutually exclusive
if ((usedMask & mask) == 0) {
// then they form a valid half subset whose sum is 2 * sideLen,
// that can be further partitioned into two equal subsets (usedMask and mask)
int validHalf = usedMask | mask;
validHalfSubsets[validHalf] = true;
// if in the past we concluded that the other half is also a valid
// half subset, DONE!
if (validHalfSubsets[all ^ validHalf])
return true;
}
}
usedMasks.push_back(mask);
}
}
return false;
} Map<Integer, Boolean> map = new HashMap();
public boolean makesquare(int[] nums) {
int sum = 0;
for (int num : nums) sum += num;
if (sum % 4 != 0 || sum == 0) return false;
sum >>>= 2;
Arrays.sort(nums);
return canMatch(nums, sum, 0, 0, 0);
}
private boolean canMatch(int[] nums, int target, int sum, int vis, int count) {
if (count == 4) return true;
if (map.containsKey(vis)) return map.get(vis);
for (int i = 0; i < nums.length; i++) {
if ((vis >>> i & 1) == 1 || sum + nums[i] > target) continue;
if (sum + nums[i] == target)
if (canMatch(nums, target, 0, vis ^ (1 << i), count + 1)) {
map.put(vis, true);
return true;
}
if (canMatch(nums, target, sum + nums[i], vis ^ (1 << i), count)) {
map.put(vis, true);
return true;
}
}
map.put(vis, false);
return false;
}
DP, you can say this is DP, but it's actually more like 2^n exponential time brute force. Although it's exponential, as wiki says, it still pass OJ, and relatively fast because of the small data, which is less than 15.
This solution is inspired by a ACM dashen. )
public boolean makesquare(int[] nums) {
int sum = 0, n = nums.length;
for (int num : nums) sum += num;
if (sum == 0 || n == 0 || (sum & 0b11) != 0) return false;
sum >>>= 2;
boolean[] dp = new boolean[1 << n];
List<Integer> parts = new ArrayList();
int all = (1 << n) - 1; // all possible choices
// try all choices, 1 mask is 1 choice
// time complexity O(2^n)
for (int mask = 0; mask <= all; mask++) {
int tmp = 0;
for (int i = 0; i < n; i++) { // retrieve "1", choose num at i
if (((mask >>> i) & 1) == 1)
tmp += nums[i];
}
if (tmp == sum) { // check whether it is valid
for (int x : parts) {
// check whether the new choice is conflit with others
if ((mask & x) == 0) {
// if there is an exist mask x has no conflit with current mask
// mark their combination "mask1 + mask2" as true
dp[mask | x] = true;
// check whether there is another "mask3 + mask4" is valid
// if there is, return true
if (dp[all ^ (mask | x)]) {
return true;
}
}
}
// record every kinds of equal-to-sum combination
parts.add(mask);
}
}
return false;
}
http://www.cnblogs.com/grandyang/p/6238425.html
其实这题还有迭代的方法,很巧妙的利用到了位操作的特性,前面的基本求和跟判断还是一样,然后建立一个变量all,初始化为(1 << n) - 1,这是什么意思呢,all其实是一个mask,数组中有多少个数字,all就有多少个1,表示全选所有的数字,然后变量target表示一条边的长度。我们建立两个一位向量masks和validHalf,其中masks保存和target相等的几个数字位置的mask,validHalf保存某个mask是否是总和的一半。然后我们从0遍历到all,实际上就是遍历所有子数组,然后我们根据mask来计算出子数组的和,注意这里用了15,而不是32,因为题目中说了数组元素个数不会超过15个。我们算出的子数组之和如果等于一条边的长度target,我们遍历masks数组中其他等于target的子数组,如果两个mask相与不为0,说明有公用的数字,直接跳过;否则将两个mask或起来,说明我们当前选的数字之和为数组总和的一半,更新validHalf的对应位置,然后我们通过all取出所有剩下的数组,并在validHalf里查找,如果也为true,说明我们成功的找到了四条边
bool makesquare(vector<int>& nums) { if (nums.empty() || nums.size() < 4) return false; int sum = accumulate(nums.begin(), nums.end(), 0); if (sum % 4 != 0) return false; int n = nums.size(), all = (1 << n) - 1, target = sum / 4; vector<int> masks, validHalf(1 << n, false); for (int i = 0; i <= all; ++i) { int curSum = 0; for (int j = 0; j <= 15; ++j) { if ((i >> j) & 1) curSum += nums[j]; } if (curSum == target) { for (int mask : masks) { if ((mask & i) != 0) continue; int half = mask | i; validHalf[half] = true; if (validHalf[all ^ half]) return true; } masks.push_back(i); } } return false; }http://bookshadow.com/weblog/2016/12/18/leetcode-matchsticks-to-square/
记忆化搜索
利用辅助数组dp[i][j]记录是否可以用火柴棍数组i,拼接成j条长度相等的边。
def makesquare(self, nums): """ :type nums: List[int] :rtype: bool """ if sum(nums) % 4: return False self.q = sum(nums) / 4 self.dp = collections.defaultdict(lambda: collections.defaultdict()) return self.solve(nums, 4) def solve(self, nums, part): total = sum(nums) if part == 1: return total == self.q size = len(nums) if size < part or total % part: return False tnums = tuple(nums) if part in self.dp[tnums]: return self.dp[tnums][part] for x in range(1, (1 << size) - 1): left, right = [], [] for y in range(size): if x & (1 << y): left.append(nums[y]) else: right.append(nums[y]) if sum(left) != self.q: continue if self.solve(right, part - 1): self.dp[tnums][part] = True return True self.dp[tnums][part] = False return False
X.
https://discuss.leetcode.com/topic/72103/simple-recursion-java-solution-66ms
Since it is square, the basic idea is get width of each side(total 4 sides) and use recursive way to figure out which group each matchstick belongs.
public boolean makesquare(int[] nums) {
Long sum=0l;
for(int x:nums){
sum=sum+x;
}
if(sum%4!=0||nums.length<4) return false;
long width=(sum/4);
Arrays.sort(nums);
long sum1=0,sum2=0,sum3=0,sum4=0;
return helper(nums,nums.length-1,sum1,sum2,sum3,sum4,width);
}
public boolean helper(int[] a, int i,long sum1,long sum2,long sum3,long sum4, long width){
if(sum1>width||sum2>width||sum3>width||sum4>width) return false;
if(i==-1){
if(sum1==width&&sum2==width&&sum3==width&&sum4==width) return true;
else return false;
}
//check a[i] belonging to side1,side2,side3,side4
return helper(a,i-1,sum1+a[i],sum2,sum3,sum4,width)||
helper(a,i-1,sum1,sum2+a[i],sum3,sum4,width)||
helper(a,i-1,sum1,sum2,sum3+a[i],sum4,width)||
helper(a,i-1,sum1,sum2,sum3,sum4+a[i],width);
}if (sum % 4 != 0) {return false;}int average = (int) sum / 4;if (nums[nums.length - 1] > average) {return false;}
X. DP
https://leetcode.com/articles/matchsticks-to-square/
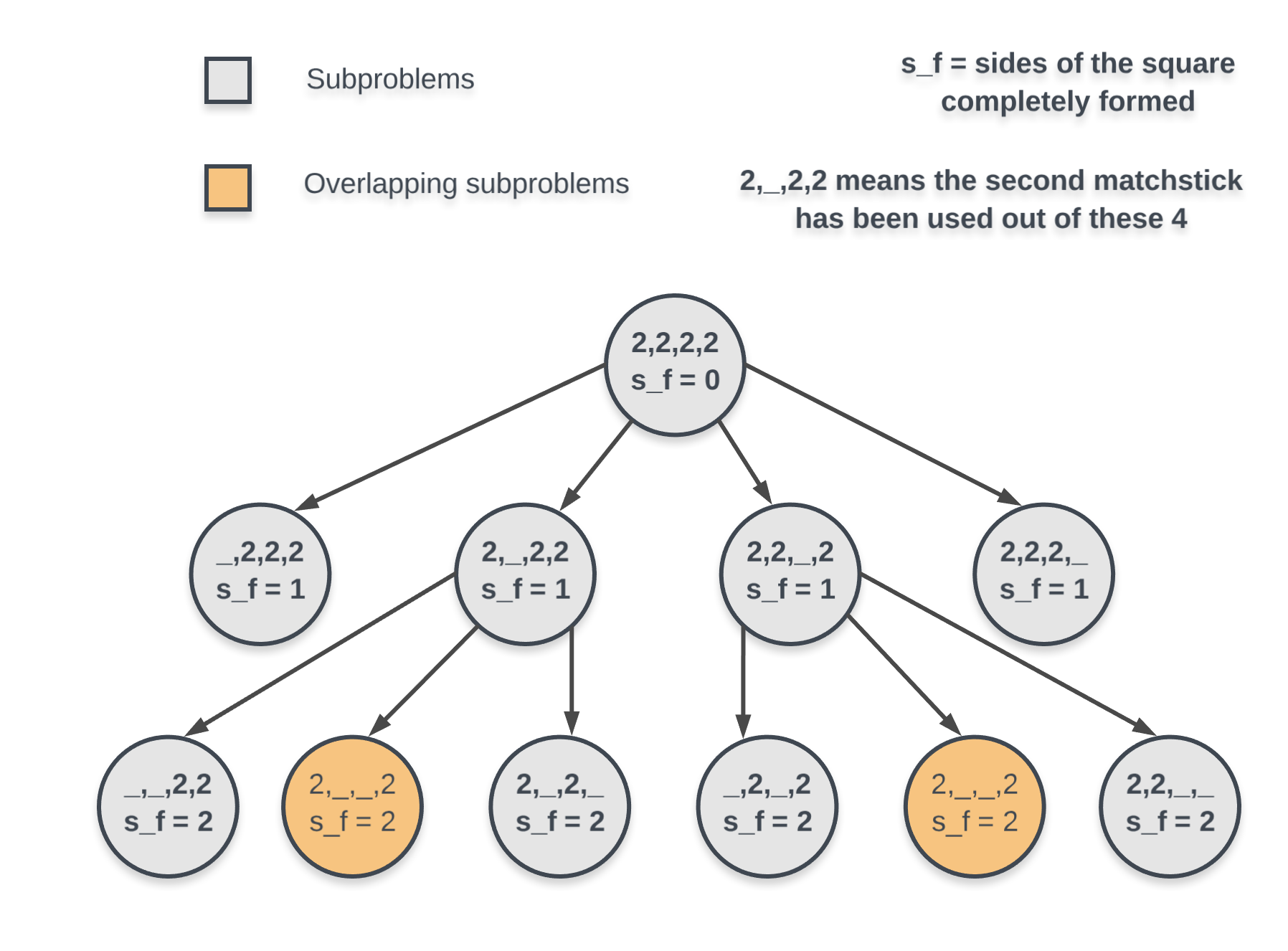
In any dynamic programming problem, what's important is that our problem must be breakable into smaller subproblems and also, these subproblems show some sort of overlap which we can save upon by caching or memoization.
Suppose we have
3,3,4,4,5,5 as our matchsticks that have been used already to construct some of the sides of our square (Note: not all the sides may be completely constructed at all times.)
If the square side is , then there are many possibilities for how the sides can be constructed using the matchsticks above. We can have
(4, 4), (3, 5), (3, 5) -----------> 3 sides fully constructed. (3, 4), (3, 5), (4), (5) ---------> 0 sides completely constructed. (3, 3), (4, 4), (5), (5) ---------> 1 side completely constructed.
As we can see above, there are multiple ways to use the same set of matchsticks and land up in completely different recursion states.
This means that if we just keep track of what all matchsticks have been used and which all are remaining, it won't properly define the state of recursion we are in or what subproblem we are solving.
A single set of used matchsticks can represent multiple different unrelated subproblems and that is just not right.
We also need to keep track of number of sides of the square that have been completely formed till now.
Also, an important thing to note in the example we just considered was that if the matchsticks being used are and the side of the square is
8, then we will always consider that arrangement that forms the most number of complete sides over that arrangement that leads to incomplete sides. Hence, the optimal arrangement here is with 3 complete sides of the square.
Let us take a look at the following recursion tree to see if in-fact we can get overlapping subproblems.

Note: Not all subproblems have been shown in this figure. The thing we wanted to point out was overlapping subproblems.
We know that the overall sum of these matchsticks can be split equally into 4 halves. The only thing we don't know is if 4 equal halves can be carved out of the given set of matchsticks. For that also we need to keep track of the number of sides completely formed at any point in time. If we end up forming 4 equal sides successfully then naturally we would have used up all of the matchsticks each being used exactly once and we would have formed a square.
Let us first look at the pseudo-code for this problem before looking at the exact implementation details for the same.
let square_side = sum(matchsticks) / 4
func recurse(matchsticks_used, sides_formed) {
if sides_formed == 4, then {
Square Formed!!
}
for match in matchsticks available, do {
add match to matchsticks_used
let result = recurse(matchsticks_used, sides_formed)
if result == True, then {
return True
}
remove match from matchsticks_used
}
return False
}
This is the overall structure of our dynamic programming solution. Of-course, a lot of implementation details are missing here that we will address now.
Implementation Details
It is very clear from the pseudo-code above that the state of a recursion is defined by two variables
matchsticks_used and sides_formed. Hence, these are the two variables that will be used to memoizeor cache the results for that specific subproblem.
The question however is how do we actually store all the matchsticks that have been used? We want a memory efficient solution for this.
If we look at the question's constraints, we find that the max number of matchsticks we can have are . That's a pretty small number and we can make use of this constraint.
All we need to store is which of the matchsticks from the original list have been used.
We can use a Bit-Map for this
We will use number of bits, one for each of the matchsticks ( is at max 15 according to the question's constraints). Initially we will start with a bit mask of
all 1s and then as we keep on using the matchsticks, we will keep on setting their corresponding bits to 0.
This way, we just have to hash an integer value which represents our bit-map and the max value for this mask would be .
Do we really need to see if all 4 sides have been completely formed ?
Another implementation trick that helps optimize this solution is that we don't really need to see if 4 sides have been completely formed.
This is because, we already know that the sum of all the matchsticks is divisible by 4. So, if 3 equal sides have been formed by using some of the matchsticks, then the remaining matchsticks would definitely form the remaining side of our square.
Hence, we only need to check if 3 sides of our square can be formed or not.
- Time Complexity : . At max unique bit masks are possible and during every recursive call, we iterate our original matchsticks array to sum up the values of matchsticks used to update the
sides_formedvariable. - Space Complexity : because is the stack space taken up by recursion and = is the max possible size of our cache for memoization.
- The size of the cache is defined by the two variables
sides_formedandmask. The number of different values thatsides_formedcan take = 4 and number of unique values ofmask= .
- The size of the cache is defined by the two variables
// The memoization cache to be used during recursion.
public HashMap<Pair<Integer, Integer>, Boolean> memo;
// Array containing our matchsticks.
public int[] nums;
// Possible side of our square depending on the total sum of all the
// matchsticks.
public int possibleSquareSide;
// Default constructor to initialise our memo cache.
public Solution() {
this.memo = new HashMap<Pair<Integer, Integer>, Boolean>();
}
// Main DP function.
public boolean recurse(Integer mask, Integer sidesDone) {
int total = 0;
int L = this.nums.length;
// The memo key for this recursion
Pair<Integer, Integer> memoKey = new Pair(mask, sidesDone);
// Find out the sum of matchsticks used till now.
for (int i = L - 1; i >= 0; i--) {
if ((mask & (1 << i)) == 0) {
total += this.nums[L - 1 - i];
}
}
// If the sum if divisible by our square's side, then we increment our number of
// complete sides formed variable.
if (total > 0 && total % this.possibleSquareSide == 0) {
sidesDone++;
}
// Base case.
if (sidesDone == 3) {
return true;
}
// Return precomputed results
if (this.memo.containsKey(memoKey)) {
return this.memo.get(memoKey);
}
boolean ans = false;
int c = total / this.possibleSquareSide;
// Remaining vlength in the current partially formed side.
int rem = this.possibleSquareSide * (c + 1) - total;
// Try out all remaining options (that are valid)
for (int i = L - 1; i >= 0; i--) {
if (this.nums[L - 1 - i] <= rem && (mask & (1 << i)) > 0) {
if (this.recurse(mask ^ (1 << i), sidesDone)) {
ans = true;
break;
}
}
}
// Cache the computed results.
this.memo.put(memoKey, ans);
return ans;
}
public boolean makesquare(int[] nums) {
// Empty matchsticks.
if (nums == null || nums.length == 0) {
return false;
}
// Find the perimeter of the square (if at all possible)
int L = nums.length;
int perimeter = 0;
for (int i = 0; i < L; i++) {
perimeter += nums[i];
}
int possibleSquareSide = perimeter / 4;
if (possibleSquareSide * 4 != perimeter) {
return false;
}
this.nums = nums;
this.possibleSquareSide = possibleSquareSide;
return this.recurse((1 << L) - 1, 0);
}