https://leetcode.com/problems/binary-tree-coloring-game/
Two players play a turn based game on a binary tree. We are given the
root of this binary tree, and the number of nodes n in the tree. n is odd, and each node has a distinct value from 1 to n.
Initially, the first player names a value
x with 1 <= x <= n, and the second player names a value y with 1 <= y <= n and y != x. The first player colors the node with value x red, and the second player colors the node with value y blue.
Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an uncolored neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)
If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.
You are the second player. If it is possible to choose such a
y to ensure you win the game, return true. If it is not possible, return false.
Example 1:
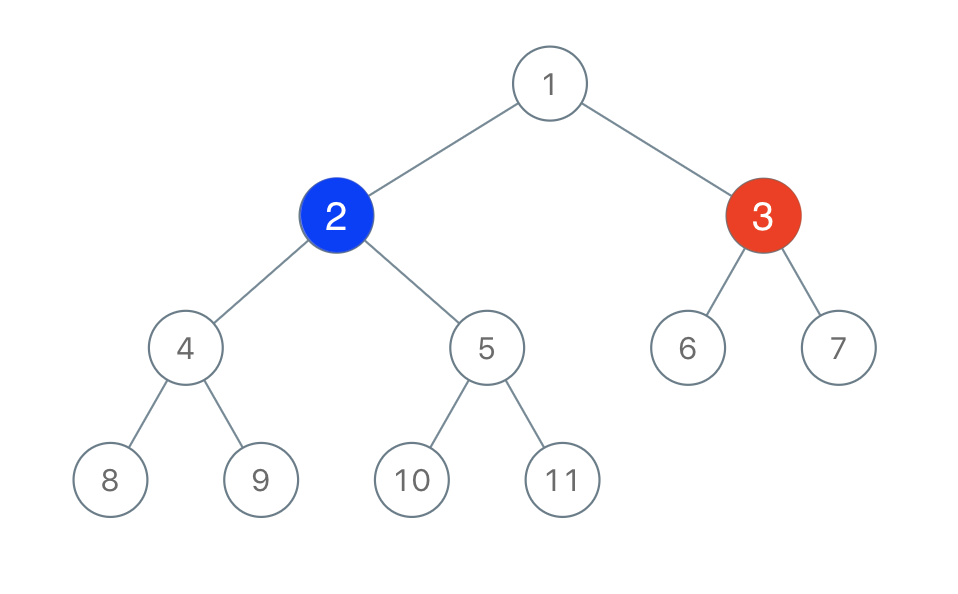
Input: root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3 Output: true Explanation: The second player can choose the node with value 2.
Constraints:
rootis the root of a binary tree withnnodes and distinct node values from1ton.nis odd.1 <= x <= n <= 100
The first player colors a node,
there are at most 3 nodes connected to this node.
Its left, its right and its parent.
Take this 3 nodes as the root of 3 subtrees.
there are at most 3 nodes connected to this node.
Its left, its right and its parent.
Take this 3 nodes as the root of 3 subtrees.
The second player just color any one root,
and the whole subtree will be his.
And this is also all he can take,
since he cannot cross the node of the first player.
and the whole subtree will be his.
And this is also all he can take,
since he cannot cross the node of the first player.
Explanation
count will recursively count the number of nodes,in the left and in the right.
n - left - right will be the number of nodes in the "subtree" of parent.Now we just need to compare
max(left, right, parent) and n / 2Complexity
Time
Space
O(N)Space
O(height) for recursion int left, right, val;
public boolean btreeGameWinningMove(TreeNode root, int n, int x) {
val = x;
count(root);
return Math.max(Math.max(left, right), n - left - right - 1) > n / 2;
}
private int count(TreeNode node) {
if (node == null) return 0;
int l = count(node.left), r = count(node.right);
if (node.val == val) {
left = l;
right = r;
}
return l + r + 1;
}Fun Moment of Follow-up:
Alex and Lee are going to play this turned based game.
Alex draw the whole tree.
Now Lee says he want to color the first node.
Alex draw the whole tree.
root and n will be given.Now Lee says he want to color the first node.
- Return
trueif Lee can ensure his win, otherwise returnfalse - Could you find the set all the nodes, that Lee can ensure he wins the game?
- What is the complexity of your solution?
For the follow up:
Calculate the count of three parts(left, right, parent) for each node. Then if any sum of two parts among above three is larger than the rest, then Lee can ensure his win on this node.
Because Lee choose this node, whichever Alex choose, left, right or parent, it will be smaller than the sum of left two parts, in this case, Alex is always lose.
https://leetcode.com/problems/binary-tree-coloring-game/discuss/367682/Simple-Clean-Java-Solution
When you find the selected node, there are three different paths you can block:
left right parent In order to guarantee your win, one of those paths should include more nodes than the sum of other two paths.
.
public boolean btreeGameWinningMove(TreeNode root, int n, int x) {
if(root == null) return false;
if(root.val == x){
int left = count(root.left);
int right = count(root.right);
int parent = n - (left+right+1);
return parent > (left + right) || left > (parent + right) || right > (left + parent);
}
return btreeGameWinningMove(root.left, n, x) || btreeGameWinningMove(root.right, n, x);
}
private int count(TreeNode node){
if(node == null) return 0;
return count(node.left) + count(node.right) + 1;
}https://leetcode.com/problems/binary-tree-coloring-game/discuss/380525/Java-Solution-with-explanation
CASE 1
We calcaulate the number of nodes in the subtree rooted at
We calcaulate the number of nodes in the subtree rooted at
X, and if the number of nodes in in this subtree is greater then the count of rest of the nodes in the tree we return false.
CASE 2
In this approach, we calcaculate the number of nodes in the left and right sub tree of the tree rooted at
In this approach, we calcaculate the number of nodes in the left and right sub tree of the tree rooted at
X, now comes the tricky part, we would choose the maximumOf(leftSubtreeCount, rightSubtreeCount) as Y. Now since Y is one of the child of X, so the nodes above X would be coloured by X. In short,Count of X = mininmumOf(leftSubtreeCount, rightSubtreeCount) + rest of the nodes in tree
Counf of Y = maximumOf(leftSubtreeCount, rightSubtreeCount)
if(Count of X < Count of Y){
return true;
}
In the end with return the
OR of the cases.
CODE
class Solution {
public boolean btreeGameWinningMove(TreeNode root, int n, int x) {
// Case 1
TreeNode nodex = findX(root, x);
int countofx = countNodes(nodex);
int countofy = n - countofx;
boolean case1 = countofy>countofx;
//Case 2
boolean case2 = helper(root,x,n,0);
return case1 || case2;
}
public static boolean helper(TreeNode root, int x, int n, int count){
if(root==null){
return false;
}
if(root.val == x){
int leftsubtree = countNodes(root.left);
int rightsubtree = countNodes(root.right);
int temp = Math.min(rightsubtree,leftsubtree) + n-(rightsubtree+leftsubtree+1);
return temp < Math.max(leftsubtree,rightsubtree);
}
boolean l = helper(root.left, x, n, count+1);
boolean r = helper(root.right, x, n, count+1);
return l||r;
}
//Method to find the node with value X
public static TreeNode findX(TreeNode root, int x){
if(root==null){
return null;
}
if(root.val == x){
return root;
}
TreeNode lft = findX(root.left,x);
if(lft!=null){
return lft;
}
return findX(root.right,x);
}
//Method to count number of nodes
public static int countNodes(TreeNode root){
if(root==null){
return 0;
}
return 1+ countNodes(root.left)+countNodes(root.right);
} // 三个部分的最大值
int maxCount = 0;
// 记录二叉树每个节点DFS的值
int[] sizeOfNode = new int[150];
// dfs 做法
// 叶子节点置为1 其父节点为子节点之和+1
int dfs(TreeNode root, int x) {
int v = root.val;
sizeOfNode[v] = 1;
if (root.left != null) {
int c = dfs(root.left, x);
sizeOfNode[v] += c;
// 如果当前节点为对方选取点, c就表示是其左子节点DFS的值
if (x == v) {
maxCount = Math.max(maxCount, c);
}
}
if (root.right != null) {
int c = dfs(root.right, x);
sizeOfNode[v] += c;
// 如果当前节点为对方选取点, c就表示是其右子节点DFS的值
if (x == v) {
maxCount = Math.max(maxCount, c);
}
}
return sizeOfNode[v];
}
public boolean btreeGameWinningMove(TreeNode root, int n, int x) {
// 对二叉树进行DFS
dfs(root, x);
// 比对父节点 与左右子节点的最大值
maxCount = Math.max(maxCount, n-sizeOfNode[x]);
// 如果己方遍历节点数大于 n/2 则对方必然小于己方
return maxCount > n/2;
}https://www.acwing.com/solution/LeetCode/content/3430/
有两位玩家参与了一场在二叉树上进行的回合制游戏。游戏中,给出二叉树的根结点
root,树上总共有 n 个结点,且 n 为奇数,其中每个结点上的值从 1 到 n 各不相同。
最开始时,一号玩家取一个值
一号玩家给值为
x 满足 1 <= x <= n,二号玩家也取一个值 y 满足 1 <= y <= n 且 y != x。一号玩家给值为
x 的结点染上红色,而二号玩家给值为 y 的结点染上蓝色。
之后两位玩家轮流进行操作,每一回合,玩家选择一个他之前涂好颜色结结点,将所选结点一个 未着色 的邻结点(即左右子结点、或父结点)进行染色。
如果当前玩家无法找到这样的结点来染色时,他的回合就会被跳过。
若两个玩家都没有可以染色的结点时,游戏结束。着色结点最多的那位玩家获得胜利️。
现在,假设你是二号玩家,根据所给出的输入,假如存在一个
y 值可以确保你赢得这场游戏,则返回 true;若无法获胜,就请返回 false。- 二叉树的根结点为
root,树上由n个结点,结点上的值从1到n各不相同。 n为奇数。1 <= x <= n <= 100
(贪心,深度优先遍历)
- 对于二号玩家,最多有三个备选的位置,一个是
x的左结点,一个是右结点,或者是父结点。 - 我们通过一次深度优先遍历,求出
x左右子树的大小,以及除了x为根的子树之外的大小,就分别可以得到三个备选所代表的被蓝色染色结点个数。 - 找到最大结点数的备选位置即可。
时间复杂度
- 每个位置仅访问一次,故时间复杂度为 。
空间复杂度
- 由于采用了递归,系统需要消耗 的空间复杂度,其中 h 为树的最大高度。
int solve(TreeNode* rt, int n, int x, int& tot) {
if (rt == NULL)
return 0;
int ls = solve(rt -> left, n, x, tot);
int rs = solve(rt -> right, n, x, tot);
if (rt -> val == x)
tot = max(max(ls, rs), n - ls - rs - 1);
return ls + rs + 1;
}
bool btreeGameWinningMove(TreeNode* root, int n, int x) {
int tot = 0;
solve(root, n, x, tot);
return tot > n / 2;
}