https://leetcode.com/problems/can-i-win/
https://discuss.leetcode.com/topic/68896/java-solution-using-hashmap-with-detailed-explanation
In Java, to denote
public boolean canIWin(int maxChoosableInteger, int desiredTotal) { if (desiredTotal<=0) return true; //如果1到最大能选的值所有和都不能满足目标值,那么肯定失败 if (maxChoosableInteger*(maxChoosableInteger+1)/2<desiredTotal) return false; char state[] = new char[maxChoosableInteger]; //maybe just int or boolean array for(int i=0;i<maxChoosableInteger;i++) state[i] = '0'; return dfs(desiredTotal, state, new HashMap<>()); } private boolean dfs(int total, char[] state, HashMap<String, Boolean> hashMap) { String key= new String(state); if (hashMap.containsKey(key)) return hashMap.get(key); for (int i=0;i<state.length;i++) { if (state[i]=='0') { state[i]='1'; if (total<=i+1 || !dfs(total-(i+1), state, hashMap)) { hashMap.put(key, true); state[i]='0'; return true; } state[i]='0'; } } hashMap.put(key, false); return false; }
http://bookshadow.com/weblog/2016/11/20/leetcode-can-i-win/
http://guoyc.com/post/can_i_win/
In the "100 game," two players take turns adding, to a running total, any integer from 1..10. The player who first causes the running total to reach or exceed 100 wins.
What if we change the game so that players cannot re-use integers?
For example, two players might take turns drawing from a common pool of numbers of 1..15 without replacement until they reach a total >= 100.
Given an integer
maxChoosableInteger and another integer desiredTotal, determine if the first player to move can force a win, assuming both players play optimally.
You can always assume that
maxChoosableInteger will not be larger than 20 and desiredTotal will not be larger than 300.
Example
Input: maxChoosableInteger = 10 desiredTotal = 11 Output: false Explanation: No matter which integer the first player choose, the first player will lose. The first player can choose an integer from 1 up to 10. If the first player choose 1, the second player can only choose integers from 2 up to 10. The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal. Same with other integers chosen by the first player, the second player will always win.
public boolean canIWin(int choose, int total) {
if (choose>=total)
return true;
if (choose*(choose+1)/2<total)
return false;
# 这里用一个Boolean的数组来做的memory,比map要快很多,但空间也用的多了
Boolean memo[] = new Boolean[1<<(choose+1)];
return dp(0, 0, choose, total, memo);
}
private boolean dp(int cur, int used, int choose, int total, Boolean[] memo) {
if (memo[used]!=null)
return memo[used];
for (int i=choose; i>0; i--) {
if ((used&(1<<i))==0) {
if (cur+i>=total) {
memo[used] = true;
return true;
}
if (!dp(cur+i, used|(1<<i), choose, total, memo)) {
memo[used] = true;
return true;
}
}
}
memo[used] = false;
return false;
}
http://www.cnblogs.com/grandyang/p/6103525.html
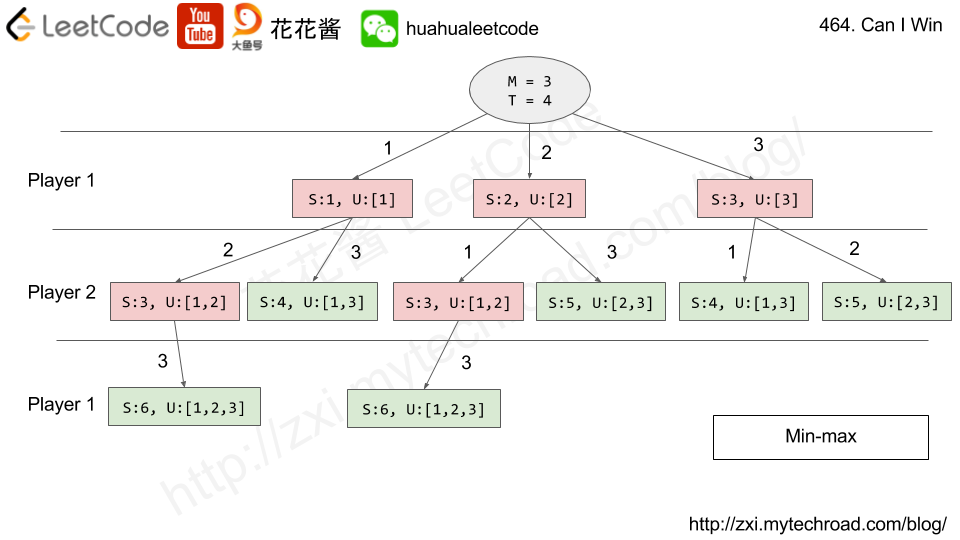
这道题给了我们一堆数字,然后两个人,每人每次选一个数字,看数字总数谁先到给定值,有点像之前那道Nim Game,但是比那题难度大。我刚开始想肯定说用递归啊,结果写完发现TLE了,后来发现我们必须要优化效率,使用HashMap来记录已经计算过的结果。我们首先来看如果给定的数字范围大于等于目标值的话,直接返回true。如果给定的数字总和小于目标值的话,说明谁也没法赢,返回false。然后我们进入递归函数,首先我们查找当前情况是否在哈希表中存在,有的话直接返回即可。我们使用一个整型数按位来记录数组中的某个数字是否使用过,我们遍历所有数字,将该数字对应的mask算出来,如果其和used相与为0的话,说明该数字没有使用过,我们看如果此时的目标值小于等于当前数字,说明已经赢了,或者我们调用递归函数,如果返回false,说明也是第一个人赢了。为啥呢,因为当前我们已经选过数字了,此时就该对第二个人调用递归函数,只有他的结果是false,我们才能赢,所以此时我们标记true,返回true。如果遍历完所有数字,我们标记false,返回false
bool canIWin(int maxChoosableInteger, int desiredTotal) { if (maxChoosableInteger >= desiredTotal) return true; if (maxChoosableInteger * (maxChoosableInteger + 1) / 2 < desiredTotal) return false; unordered_map<int, bool> m; return canWin(maxChoosableInteger, desiredTotal, 0, m); } bool canWin(int length, int total, int used, unordered_map<int, bool>& m) { if (m.count(used)) return m[used]; for (int i = 0; i < length; ++i) { int cur = (1 << i); if ((cur & used) == 0) { if (total <= i + 1 || !canWin(length, total - (i + 1), cur | used, m)) { m[used] = true; return true; } } } m[used] = false; return false; }
After solving several "Game Playing" questions in leetcode, I find them to be pretty similar. Most of them can be solved using the top-down DP approach, which "brute-forcely" simulates every possible state of the game.
The key part for the top-down dp strategy is that we need to avoid repeatedly solving sub-problems. Instead, we should use some strategy to "remember" the outcome of sub-problems. Then when we see them again, we instantly know their result. By doing this, we can always reduce time complexity from exponential to polynomial.
(EDIT: Thanks for @billbirdh for pointing out the mistake here. For this problem, by applying the memo, we at most compute for every subproblem once, and there are
(EDIT: Thanks for @billbirdh for pointing out the mistake here. For this problem, by applying the memo, we at most compute for every subproblem once, and there are
O(2^n) subproblems, so the complexity is O(2^n) after memorization. (Without memo, time complexity should be like O(n!))
For this question, the key part is:
what is the state of the game? Intuitively, to uniquely determine the result of any state, we need to know:- The unchosen numbers
- The remaining desiredTotal to reach
A second thought reveals that 1) and 2) are actually related because we can always get the 2) by deducting the sum of chosen numbers from original desiredTotal.
Then the problem becomes how to describe the state using 1).
In my solution, I use a boolean array to denote which numbers have been chosen, and then a question comes to mind, if we want to use a Hashmap to remember the outcome of sub-problems, can we just use
Map<boolean[], Boolean> ? Obviously we cannot, because the if we use boolean[] as a key, the reference to boolean[] won't reveal the actual content in boolean[].
Since in the problem statement, it says
maxChoosableInteger will not be larger than 20, which means the length of our boolean[] array will be less than 20. Then we can use an Integer to represent this boolean[] array. How?
Say the boolean[] is
{false, false, true, true, false}, then we can transfer it to an Integer with binary representation as 00110. Since Integer is a perfect choice to be the key of HashMap, then we now can "memorize" the sub-problems using Map<Integer, Boolean>.
The rest part of the solution is just simulating the game process using the top-down dp.
In Java, to denote
boolean[], an easier way is to use Arrays.toString(boolean[]), which will transfer a boolean[] to sth like "[true, false, false, ....]", which is also not limited to how maxChoosableInteger is set, so it can be generalized to arbitrary large maxChoosableInteger. public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
if (desiredTotal<=0) return true;
if (maxChoosableInteger*(maxChoosableInteger+1)/2<desiredTotal) return false;
return canIWin(desiredTotal, new int[maxChoosableInteger], new HashMap<>());
}
private boolean canIWin(int total, int[] state, HashMap<String, Boolean> hashMap) {
String curr=Arrays.toString(state);
if (hashMap.containsKey(curr)) return hashMap.get(curr);
for (int i=0;i<state.length;i++) {
if (state[i]==0) {
state[i]=1;
if (total<=i+1 || !canIWin(total-(i+1), state, hashMap)) {
hashMap.put(curr, true);
state[i]=0;
return true;
}
state[i]=0;
}
}
hashMap.put(curr, false);
return false;
}public boolean canIWin(int maxChoosableInteger, int desiredTotal) { if (desiredTotal<=0) return true; //如果1到最大能选的值所有和都不能满足目标值,那么肯定失败 if (maxChoosableInteger*(maxChoosableInteger+1)/2<desiredTotal) return false; char state[] = new char[maxChoosableInteger]; //maybe just int or boolean array for(int i=0;i<maxChoosableInteger;i++) state[i] = '0'; return dfs(desiredTotal, state, new HashMap<>()); } private boolean dfs(int total, char[] state, HashMap<String, Boolean> hashMap) { String key= new String(state); if (hashMap.containsKey(key)) return hashMap.get(key); for (int i=0;i<state.length;i++) { if (state[i]=='0') { state[i]='1'; if (total<=i+1 || !dfs(total-(i+1), state, hashMap)) { hashMap.put(key, true); state[i]='0'; return true; } state[i]='0'; } } hashMap.put(key, false); return false; }
http://bookshadow.com/weblog/2016/11/20/leetcode-can-i-win/
记忆化搜索 + 位运算
由于maxChoosableInteger不大于20,因此可以通过整数state表示当前已经选择了哪些数字
state的第i位为1时,表示选择了数字i + 1
利用字典dp记录已经搜索过的状态
https://discuss.leetcode.com/topic/78928/brute-force-and-memoization- O(n!) brute force, n is maxChoosableInteger. T(n)=nT(n-1)
bool canIWin(int maxChoosableInteger, int desiredTotal) {
if(!desiredTotal) return 1;
return canWin(~0<<maxChoosableInteger, maxChoosableInteger, desiredTotal);
}
bool canWin(int pool, int maxint, int tot) {
if(tot<=0) return 0;
for(int i=0;i<maxint;i++) {
int mask = 1<<i;
if(pool & mask) continue;
pool|=mask;
if(!canWin(pool,maxint, tot-i-1)) return 1;
pool^=mask;
}
return 0;
}
- O(2^n) Memoization. There is redundant computation in #1. A state with a pool and total may be computed many times. So we can cache the state and reuse it. At first glance, it seems that a state is determined by two values, the pool and the total. However, since the initial total is known, the remaining total is known given the pool. So a state can be identified by the pool only.
bool canIWin(int maxChoosableInteger, int desiredTotal) {
if(!desiredTotal) return 1;
if(maxChoosableInteger*(maxChoosableInteger+1)/2<desiredTotal) return 0;
unordered_map<int,char> mem;
return canWin(~0<<maxChoosableInteger, maxChoosableInteger, desiredTotal, mem);
}
bool canWin(int pool, int maxint, int tot, unordered_map<int,char>& mem) {
if(tot<=0) return 0;
auto it = mem.find(pool);
if(it != mem.end()) return it->second;
for(int i=0;i<maxint;i++) {
int mask = 1<<i;
if(pool & mask) continue;
pool|=mask;
if(!canWin(pool,maxint,tot-i-1,mem)) return mem[pool^=mask]=1;
pool^=mask;
}
return mem[pool] = 0;
}
- Iterative dp. For most dp problems, the next step is to transform recursion with memoization to iterative dp. However, that does not help and is actually pretty bad for this problem. In iterative dp, we have to visit all the 2^n states to get the result. In #2 DFS with memoization, DFS terminates as soon as it finds a way to win. The worst case O(2^n) rarely happens. So if DFS has early termination condition, then it should be better than dp that visits all the states. Similar problems are word break and Concatenated Words.
http://guoyc.com/post/can_i_win/
现在先实现数字可以重复使用的情况:
令
dp[i]表示玩家在当前和为i的情况下是否可以获胜。 choose表示玩家可以使用1~choose之间的数字。 target表示先到达target的玩家获胜。
初始情况:
dp[i]=True if (i+choose)>=target
递推公式:
dp[i]=True if dp[i+j]=False for any i+1<=j<=i+choose
返回结果:
dp[0](即先选择的玩家是否获胜) |