https://leetcode.com/problems/k-th-smallest-in-lexicographical-order/
https://discuss.leetcode.com/topic/64539/java-7ms-denary-trie-tree-solution-with-detailed-explanation
http://bookshadow.com/weblog/2016/10/24/leetcode-k-th-smallest-in-lexicographical-order/
Given integers
n and k, find the lexicographically k-th smallest integer in the range from 1 to n.
Note: 1 ≤ k ≤ n ≤ 109.
Example:
Input: n: 13 k: 2 Output: 10 Explanation: The lexicographical order is [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9], so the second smallest number is 10.https://discuss.leetcode.com/topic/64624/concise-easy-to-understand-java-5ms-solution-with-explaination
Original idea comes from
http://bookshadow.com/weblog/2016/10/24/leetcode-k-th-smallest-in-lexicographical-order/
http://bookshadow.com/weblog/2016/10/24/leetcode-k-th-smallest-in-lexicographical-order/
Actually this is a denary tree (each node has 10 children). Find the kth element is to do a k steps preorder traverse of the tree.
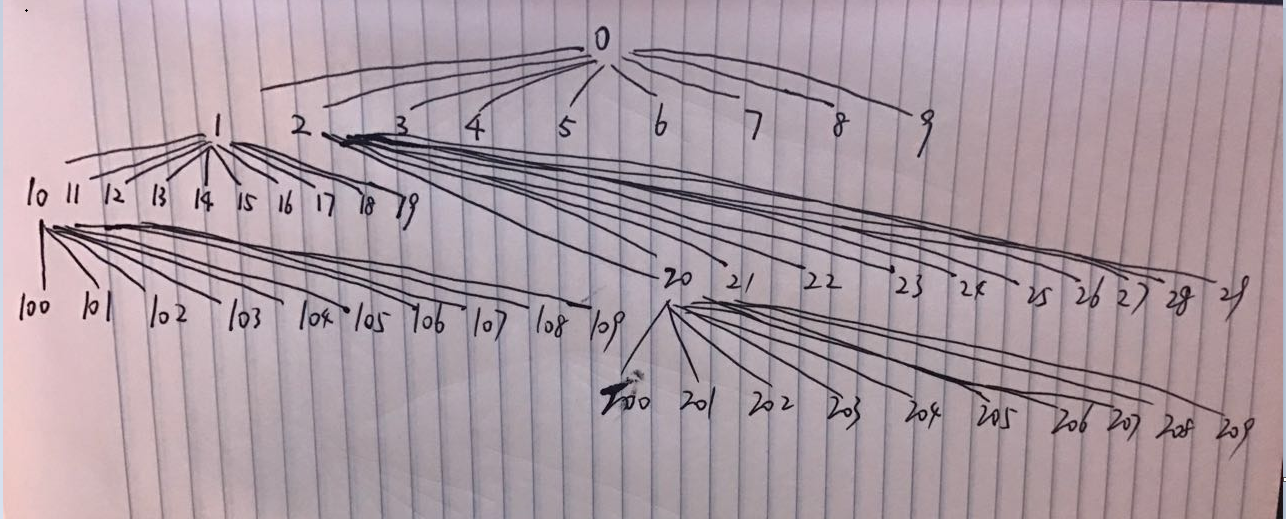

Initially, image you are at node 1 (variable: curr),
the goal is move (k - 1) steps to the target node x. (substract steps from k after moving)
when k is down to 0, curr will be finally at node x, there you get the result.
the goal is move (k - 1) steps to the target node x. (substract steps from k after moving)
when k is down to 0, curr will be finally at node x, there you get the result.
we don't really need to do a exact k steps preorder traverse of the denary tree, the idea is to calculate the steps between curr and curr + 1 (neighbor nodes in same level), in order to skip some unnecessary moves.
Main function
Firstly, calculate how many steps curr need to move to curr + 1.
Firstly, calculate how many steps curr need to move to curr + 1.
- if the steps <= k, we know we can move to curr + 1, and narrow down k to k - steps.
- else if the steps > k, that means the curr + 1 is actually behind the target node x in the preorder path, we can't jump to curr + 1. What we have to do is to move forward only 1 step (curr * 10 is always next preorder node) and repeat the iteration.
calSteps function
- how to calculate the steps between curr and curr + 1?
Here we come up a idea to calculate by level.
Let n1 = curr, n2 = curr + 1.
n2 is always the next right node beside n1's right most node (who shares the same ancestor "curr")
(refer to the pic, 2 is right next to 1, 20 is right next to 19, 200 is right next to 199). - so, if n2 <= n, what means n1's right most node exists, we can simply add the number of nodes from n1 to n2 to steps.
- else if n2 > n, what means n (the biggest node) is on the path between n1 to n2, add (n + 1 - n1) to steps.
- organize this flow to "steps += Math.min(n + 1, n2) - n1; n1 *= 10; n2 *= 10;"
https://discuss.leetcode.com/topic/64539/java-7ms-denary-trie-tree-solution-with-detailed-explanation
The solution used DFS to search in a trie tree. The trick is to skip the sub-tree if the (current index + node number of the sub-tree) is smaller than the k.
The key problem is - How to count the nodes in a sub-tree?
The trie tree was made up of two kinds of sub-tree, the complete sub-tree with each node either has ten or zero children and the incomplete sub-tree with some inner nodes can has 1 to 9 children.
The complete tree's nodes number is easy to get, it will be something like 1, 11, 111, 1111...(each node has ten children plus the root)
The incomplete tree can be calculated like the flowing example:
for n = 213, the tree will be something like this:
$
/ / / \
1 2 3 [4 ~ 9]
/\ /\ /\ /\
0, [1~9] 0, 1,[2~9] 0,[1~9] ...
/ \ / /
[0~9] ... [0~9] [0~3]
the sub-trees start with char '1' and '3'~'9' are complete trees, which '1' sub-tree with ranges in 1,10~19, 100~199 has 111 nodes and '3'~'9' each has 11 nodes (e.g. 3 with ranges in 3, 30~39).
the sub-tree starts with '2' is not full, i.e. the ranges are 2, 20~29, 200~213. But the '2' sub-tree still has a 'complete' tree like '3'~'9' with range in 2, 20~29, and we just need to add the remained leaf nodes which is (213%200)+1 or (213-200)+1.
The 200 is the most left node in the '2' sub-tree and 299 is the most right node in '2' sub-tree if it is complete.
it also showed the idea about how to judge a given sub-three is complete or incomplete:
it also showed the idea about how to judge a given sub-three is complete or incomplete:
We first assume all sub-trees are complete and test by following:
{
if (the most right node in a sub-tree is not greater than the number n)
the sub-tree is complete with nodes number = 111..(log10(n)+1 1s)
else if (the most left node in a sub-tree is greater than the number n)
the sub-tree is complete with nodes number = 11... (log10(n) 1s)
else
the sub-tree is incomplete with nodes number =
n - (the most left node in the subree) + 1 + 11... (log10(n) 1s)
}
The nodes number in a complete tree can be cached.
Then we just need to recursively decrease k by the nodes number of the skipped
sub-tree until k reached 1.
sub-tree until k reached 1.
Also be carefully the first layer is start from 1 while other layers are start from 0.
public class Solution {
int countNum(int n){
int i=0;
while(n>0){
n/=10;
i++;
}
return i;
}
int getFullTreeNum(int depth){
int sum=0, children=1;
while(depth>0){
sum+=children;
children*=10;
depth--;
}
return sum;
}
int getMax(int prefix, int depth){
while(depth>0){
prefix*=10;
prefix+=9;
depth--;
}
return prefix;
}
int getMin(int prefix, int depth){
while(depth>0){
prefix*=10;
depth--;
}
return prefix;
}
int helper(int n, int k, int prefix, int depth){
int lowNum=getFullTreeNum(depth), highNum=getFullTreeNum(depth-1);
for(int i=(prefix==0?1:0);i<=9;i++){
int nodeNum=0;
if(getMax(prefix*10+i, depth-1)<=n){
nodeNum=lowNum;
}
else if(getMin(prefix*10+i, depth-1)>n){
nodeNum=highNum;
}
else{
nodeNum=highNum+((n-getMin(prefix*10+i, depth-1))+1);
}
k-=nodeNum;
if(k<=0){
k+=nodeNum;
if(k==1){
return prefix*10+i;
}
else {
return helper(n, k-1, prefix*10+i, depth-1);
}
}
}
return 0;
}
public int findKthNumber(int n, int k) {
int depth=countNum(n);
int index=0;
return helper(n, k, 0, depth);
}
http://www.cnblogs.com/grandyang/p/6031787.html
https://discuss.leetcode.com/topic/64442/easy-to-understand-js-solution
这道题是之前那道Lexicographical Numbers的延伸,之前让按字典顺序打印数组,而这道题让我们快速定位某一个位置,那么我们就不能像之前那道题一样,一个一个的遍历,这样无法通过OJ,这也是这道题被定为Hard的原因。那么我们得找出能够快速定位的方法,我们如果仔细观察字典顺序的数组,我们可以发现,其实这是个十叉树Denary Tree,就是每个节点的子节点可以有十个,比如数字1的子节点就是10到19,数字10的子节点可以是100到109,但是由于n大小的限制,构成的并不是一个满十叉树。我们分析题目中给的例子可以知道,数字1的子节点有4个(10,11,12,13),而后面的数字2到9都没有子节点,那么这道题实际上就变成了一个先序遍历十叉树的问题,那么难点就变成了如何计算出每个节点的子节点的个数,我们不停的用k减去子节点的个数,当k减到0的时候,当前位置的数字即为所求。现在我们来看如何求子节点个数,比如数字1和数字2,我们要求按字典遍历顺序从1到2需要经过多少个数字,首先把1本身这一个数字加到step中,然后我们把范围扩大十倍,范围变成10到20之前,但是由于我们要考虑n的大小,由于n为13,所以只有4个子节点,这样我们就知道从数字1遍历到数字2需要经过5个数字,然后我们看step是否小于等于k,如果是,我们cur自增1,k减去step;如果不是,说明要求的数字在子节点中,我们此时cur乘以10,k自减1,以此类推,直到k为0推出循环,此时cur即为所求:
int findKthNumber(int n, int k) { int cur = 1; --k; while (k > 0) { long long step = 0, first = cur, last = cur + 1; while (first <= n) { step += min((long long)n + 1, last) - first; first *= 10; last *= 10; } if (step <= k) { ++cur; k -= step; } else { cur *= 10; --k; } } return cur; }
// Calculates the amount of
// numbers <= n that starts with prefix.
function countForPrefix (n, prefix) {
let a = parseInt(prefix);
let b = a + 1;
if (a > n || a === 0)
return 0;
let res = 1;
a *= 10; b *= 10;
while (a <= n) {
res += Math.min(n + 1, b) - a;
a *= 10; b *= 10;
}
return res;
}
// Constructs resulting number digit by digit
// starting with the most significant.
function findKthNumber (n, k) {
let i, prefix = '';
while (k !== 0) {
for (i = 0; i <= 9; i++) {
const count = countForPrefix(n, prefix + i);
if (count < k)
k -= count;
else
break;
}
prefix = prefix + i;
k--; // number equal to prefix
}
return parseInt(prefix, 10);
}http://bookshadow.com/weblog/2016/10/24/leetcode-k-th-smallest-in-lexicographical-order/