https://www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/the-euclidean-algorithm
http://quiz.geeksforgeeks.org/c-program-find-gcd-hcf-two-numbers/
http://www.geeksforgeeks.org/euclids-algorithm-when-and-operations-are-costly/



Not efficient:
long long gcd(long long a, long long b)
{
if (b == 0)return a;
return gcd(b, a%b);
}
long long lcm(long long a, long long b)
{
return a * b / gcd(a, b);
}
http://www.geeksforgeeks.org/gcd-two-array-numbers/
Given an array of numbers, find GCD of the array elements.
If we examine the Euclidean Algorithm we can see that it makes use of the following properties:
- GCD(A,0) = A
- GCD(0,B) = B
- If A = B⋅Q + R and B≠0 then GCD(A,B) = GCD(B,R) where Q is an integer, R is an integer between 0 and B-1
The first two properties let us find the GCD if either number is 0. The third property lets us take a larger, more difficult to solve problem, and reduce it to a smaller, easier to solve problem.
The Euclidean Algorithm makes use of these properties by rapidly reducing the problem into easier and easier problems, using the third property, until it is easily solved by using one of the first two properties.
We can understand why these properties work by proving them.
We can prove that GCD(A,0)=A is as follows:
- The largest integer that can evenly divide A is A.
- All integers evenly divide 0, since for any integer, C, we can write C ⋅ 0 = 0. So we can conclude that A must evenly divide 0.
- The greatest number that divides both A and 0 is A.
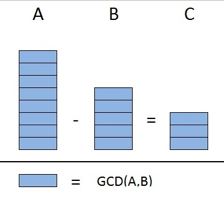
Suppose we have three integers A,B and C such that A-B=C.
Proof that the GCD(A,B) evenly divides C
The GCD(A,B), by definition, evenly divides A. As a result, A must be some multiple of GCD(A,B). i.e. X⋅GCD(A,B)=A where X is some integer
The GCD(A,B), by definition, evenly divides B. As a result, B must be some multiple of GCD(A,B). i.e. Y⋅GCD(A,B)=B where Y is some integer
A-B=C gives us:
- X⋅GCD(A,B) - Y⋅GCD(A,B) = C
- (X - Y)⋅GCD(A,B) = C
So we can see that GCD(A,B) evenly divides C.
An illustration of this proof is shown in the left portion of the figure below:
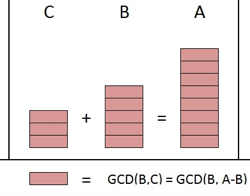
Proof that the GCD(B,C) evenly divides A
The GCD(B,C), by definition, evenly divides B. As a result, B must be some multiple of GCD(B,C). i.e. M⋅GCD(B,C)=B where M is some integer
The GCD(B,C), by definition, evenly divides C. As a result, C must be some multiple of GCD(B,C). i.e. N⋅GCD(B,C)=C where N is some integer
A-B=C gives us:
- B+C=A
- M⋅GCD(B,C) + N⋅GCD(B,C) = A
- (M + N)⋅GCD(B,C) = A
So we can see that GCD(B,C) evenly divides A.
An illustration of this proof is shown in the figure below
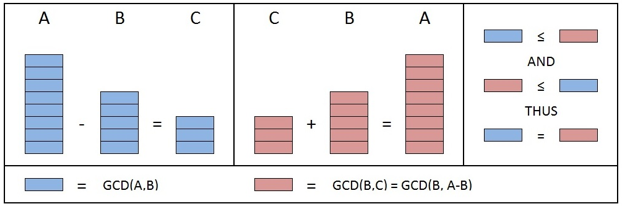
Proof that GCD(A,B)=GCD(A,A-B)
- GCD(A,B) by definition, evenly divides B.
- We proved that GCD(A,B) evenly divides C.
- Since the GCD(A,B) divides both B and C evenly it is a common divisor of B and C.
GCD(A,B) must be less than or equal to, GCD(B,C), because GCD(B,C) is the “greatest” common divisor of B and C.
- GCD(B,C) by definition, evenly divides B.
- We proved that GCD(B,C) evenly divides A.
- Since the GCD(B,C) divides both A and B evenly it is a common divisor of A and B.
GCD(B,C) must be less than or equal to, GCD(A,B), because GCD(A,B) is the “greatest” common divisor of A and B.
Given that GCD(A,B)≤GCD(B,C) and GCD(B,C)≤GCD(A,B) we can conclude that:
GCD(A,B)=GCD(B,C)
Which is equivalent to:
GCD(A,B)=GCD(B,A-B)
An illustration of this proof is shown in the right portion of the figure below.
Proof that GCD(A,B) = GCD(B,R)
We proved that GCD(A,B)=GCD(B,A-B)
The order of the terms does not matter so we can say GCD(A,B)=GCD(A-B,B)
We can repeatedly apply GCD(A,B)=GCD(A-B,B) to obtain:
GCD(A,B)=GCD(A-B,B)=GCD(A-2B,B)=GCD(A-3B,B)=...=GCD(A-Q⋅B,B)
But A= B⋅Q + R so A-Q⋅B=R
Thus GCD(A,B)=GCD(R,B)
The order of terms does not matter, thus:
GCD(A,B)=GCD(B,R)
int gcd(int a, int b){ // Everything divides 0 if (a == 0 || b == 0) return 0; // base case if (a == b) return a; // a is greater if (a > b) return gcd(a-b, b); return gcd(a, b-a);}
Version 1 (Using subtraction)
http://qiemengdao.iteye.com/blog/1660212
和欧几里德算法 算法不同的是,Stein算法只有整数的移位和加减法
gcd(a,a) = a,也就是一个数和他自身的公约数是其自身
gcd(ka,kb) = k gcd(a,b),也就是最大公约数运算和倍乘运算可以交换,特殊的,当k=2时,说明两个偶数的最大公约数必然能被2整除。
 intGcd(inta,intb)
intGcd(inta,intb)
 {
{
 if(a==0)returnb;
if(a==0)returnb;
 if(b==0)returna;
if(b==0)returna;
 if(a%2==0&&b%2==0)return2*gcd(a>>1,b>>1);
if(a%2==0&&b%2==0)return2*gcd(a>>1,b>>1);
 elseif(a%2==0)returngcd(a>>1,b);
elseif(a%2==0)returngcd(a>>1,b);
 elseif(b%2==0)returngcd(a,b>>1);
elseif(b%2==0)returngcd(a,b>>1);
 elsereturngcd(abs(a-b),Min(a,b));
elsereturngcd(abs(a-b),Min(a,b));
 }
}
考虑欧几里德算法,最恶劣的情况是,每次迭代a = 2b -1,这样,迭代后,r= b-1。如果a小于2N,这样大约需要 4N次迭代。而考虑Stein算法,每次迭代后,显然AN+1BN+1≤ ANBN/2,最大迭代次数也不超过4N次。也就是说,迭代次数几乎是相等的。但是,需要注意的是,对于大素数,试商法将使每次迭代都更复杂,因此对于大素数Stein将更有优势
Binary GCD algorithm
http://en.wikipedia.org/wiki/Binary_GCD_algorithm
Stein's algorithm uses simpler arithmetic operations than the conventional Euclidean algorithm; it replaces division with arithmetic shifts, comparisons, and subtraction.
The algorithm reduces the problem of finding the GCD by repeatedly applying these identities:
gcd(0, v) = v, because everything divides zero, and v is the largest number that divides v. Similarly, gcd(u, 0) = u. gcd(0, 0) is not typically defined, but it is convenient to set gcd(0, 0) = 0.
If u and v are both even, then gcd(u, v) = 2·gcd(u/2, v/2), because 2 is a common divisor.
If u is even and v is odd, then gcd(u, v) = gcd(u/2, v), because 2 is not a common divisor. Similarly, if u is odd and v is even, then gcd(u, v) = gcd(u, v/2).
If u and v are both odd, and u ≥ v, then gcd(u, v) = gcd((u ? v)/2, v). If both are odd and u < v, then gcd(u, v) = gcd((v ? u)/2, u). These are combinations of one step of the simple Euclidean algorithm, which uses subtraction at each step, and an application of step 3 above. The division by 2 results in an integer because the difference of two odd numbers is even.[3]
Repeat steps 2–4 until u = v, or (one more step) until u = 0. In either case, the GCD is 2kv, where k is the number of common factors of 2 found in step 2.
The algorithm requires O(n2)[4] worst-case time, where n is the number of bits in the larger of the two numbers. Although each step reduces at least one of the operands by at least a factor of 2, the subtract and shift operations take linear time for very large integers (although they're still quite fast in practice, requiring about one operation per word of the representation).
Recursive version in C
unsigned int gcd(unsigned int u, unsigned int v)
{
// simple cases (termination)
if (u == v)
return u;
if (u == 0)
return v;
if (v == 0)
return u;
// look for factors of 2
if (~u & 1) // u is even
{
if (v & 1) // v is odd
return gcd(u >> 1, v);
else // both u and v are even
return gcd(u >> 1, v >> 1) << 1;
}
if (~v & 1) // u is odd, v is even
return gcd(u, v >> 1);
// reduce larger argument
if (u > v)
return gcd((u - v) >> 1, v);
return gcd((v - u) >> 1, u);
}
Iterative version in C
It first removes all common factors of 2 using identity 2, then computes the GCD of the remaining numbers using identities 3 and 4, and combines these to form the final answer.
with implementations of binary GCD similar to the above C code, the gain in speed over the Euclidean algorithm is always less in practice than in theory. The reason is that the code uses many data-dependent branches
https://github.com/adnanaziz/EpiCode/blob/master/Java/com/epi/GCD.java
Euclid's GCD Algorithm欧几里得
http://people.cis.ksu.edu/~schmidt/301s12/Exercises/euclid_alg.html
http://en.wikipedia.org/wiki/Euclidean_algorithm
Euclid's insight was to observe that, if x > y, then
GCD(x,y) = GCD(x-y,y)
Proof:
x - y = q1d - q2d = (q1 - q2)d. Therefore d is also a divisor of x-y.
Using similar reasoning, one can show the converse, i.e., that any divisor of x-y and y is also a divisor of x. Hence, the set of common divisors of x and y is the same as the set of common divisors of x-y and y. In particular, the largest values in these two sets are the same, which is to say that GCD(x,y) = GCD(x-y,y).
int gcd(int K, int M) {
int k = K; // In order to state a simple, elegant loop invariant,
int m = M; // we keep the formal arguments constant and use
// local variables to do the calculations.
// loop invariant: GCD(K,M) = GCD(k,m)
while (k != m) {
if (k > m)
{ k = k-m; }
else
{ m = m-k; }
}
// At this point, GCD(K,M) = GCD(k,m) = GCD(k,k) = k
return k;
}
A significant improvement in performance (in some cases) is possible, however, by using the remainder operator (%) rather than subtraction.
int gcd(int K, int M) {
int k = K; // In order to state a simple, elegant loop invariant,
int m = M; // we keep the formal arguments constant and use
// local variables to do the calculations.
// loop invariant: GCD(K,M) = GCD(k,m)
while (k !=0 && m != 0) {
if (k > m)
{ k = k % m; }
else
{ m = m % k; }
}
// At this point, GCD(K,M) = GCD(k,m) = max(k,m)
return Math.max(k,m);
}
Further code-simplification improvements are possible, however, by ensuring that k ≥ m. We can achieve this by replacing, on each iteration, k's value by m's and m's by k % m. This way, no if statement is needed:
int gcd(int K, int M) {
int k = Math.max(K,M);
int m = Math.min(K,M);
// loop invariant: k ≥ m ∧ GCD(K,M) = GCD(k,m)
while (m != 0) {
int r = k % m;
k = m;
m = r;
}
// At this point, GCD(K,M) = GCD(k,m) = GCD(k,0) = k
return k;
}
http://rosettacode.org/wiki/Least_common_multiple// Recursive function to return gcd of a and bint gcd(int a, int b){ if (a == b) return a; return (a > b)? gcd(a-b, b): gcd(a, b-a);}
Version 2 (Using modulo operator)
int gcd(int a, int b){ if (a == 0) return b; return gcd(b%a, a);} |
Version 1 can take linear time to find the GCD, consider the situation when one of the given numbers is much bigger than the other. Version 2 is obviously more efficient as there are less recursive calls and takes logarithmic time.
Below are some important observations. The idea is to use bitwise operators. We can find x/2 using x>>1. We can check whether x is odd or even using x&1.
gcd(a, b) = 2*gcd(a/2, b/2) if both a and b are even.
gcd(a, b) = gcd(a/2, b) if a is even and b is odd.
gcd(a, b) = gcd(a, b/2) if a is odd and b is even.
gcd(a, b) = gcd(a/2, b) if a is even and b is odd.
gcd(a, b) = gcd(a, b/2) if a is odd and b is even.
int gcd(int a, int b){ // Base cases if (b == 0 || a == b) return a; if (a == 0) return b; // If both a and b are even, divide both a // and b by 2. And multiply the result with 2 if ( (a & 1) == 0 && (b & 1) == 0 ) return gcd(a>>1, b>>1) << 1; // If a is even and b is odd, divide a bb 2 if ( (a & 1) == 0 && (b & 1) != 0 ) return gcd(a>>1, b); // If a is odd and b is even, divide b bb 2 if ( (a & 1) != 0 && (b & 1) == 0 ) return gcd(a, b>>1); // If both are odd, then apply normal subtraction // algorithm. Note that odd-odd case always // converts odd-even case after one recursion return (a > b)? gcd(a-b, b): gcd(a, b-a);}http://qiemengdao.iteye.com/blog/1660212
和欧几里德算法 算法不同的是,Stein算法只有整数的移位和加减法
gcd(a,a) = a,也就是一个数和他自身的公约数是其自身
gcd(ka,kb) = k gcd(a,b),也就是最大公约数运算和倍乘运算可以交换,特殊的,当k=2时,说明两个偶数的最大公约数必然能被2整除。
有了上述规律就可以给出Stein算法如下:
如果A=0,B是最大公约数,算法结束
如果B=0,A是最大公约数,算法结束
设置A1 = A、B1=B和C1 = 1
如果An和Bn都是偶数,则An+1 =An /2,Bn+1 =Bn /2,Cn+1 =Cn *2(注意,乘2只要把整数左移一位即可,除2只要把整数右移一位即可)
如果An是偶数,Bn不是偶数,则An+1 =An /2,Bn+1 =Bn ,Cn+1 =Cn (很显然啦,2不是奇数的约数)
如果Bn是偶数,An不是偶数,则Bn+1 =Bn /2,An+1 =An ,Cn+1 =Cn (很显然啦,2不是奇数的约数)
如果An和Bn都不是偶数,则An+1 =|An -Bn|,Bn+1 =min(An,Bn),Cn+1 =Cn
n++,转4
如果B=0,A是最大公约数,算法结束
设置A1 = A、B1=B和C1 = 1
如果An和Bn都是偶数,则An+1 =An /2,Bn+1 =Bn /2,Cn+1 =Cn *2(注意,乘2只要把整数左移一位即可,除2只要把整数右移一位即可)
如果An是偶数,Bn不是偶数,则An+1 =An /2,Bn+1 =Bn ,Cn+1 =Cn (很显然啦,2不是奇数的约数)
如果Bn是偶数,An不是偶数,则Bn+1 =Bn /2,An+1 =An ,Cn+1 =Cn (很显然啦,2不是奇数的约数)
如果An和Bn都不是偶数,则An+1 =|An -Bn|,Bn+1 =min(An,Bn),Cn+1 =Cn
n++,转4
考虑欧几里德算法,最恶劣的情况是,每次迭代a = 2b -1,这样,迭代后,r= b-1。如果a小于2N,这样大约需要 4N次迭代。而考虑Stein算法,每次迭代后,显然AN+1BN+1≤ ANBN/2,最大迭代次数也不超过4N次。也就是说,迭代次数几乎是相等的。但是,需要注意的是,对于大素数,试商法将使每次迭代都更复杂,因此对于大素数Stein将更有优势
Binary GCD algorithm
http://en.wikipedia.org/wiki/Binary_GCD_algorithm
Stein's algorithm uses simpler arithmetic operations than the conventional Euclidean algorithm; it replaces division with arithmetic shifts, comparisons, and subtraction.
The algorithm reduces the problem of finding the GCD by repeatedly applying these identities:
gcd(0, v) = v, because everything divides zero, and v is the largest number that divides v. Similarly, gcd(u, 0) = u. gcd(0, 0) is not typically defined, but it is convenient to set gcd(0, 0) = 0.
If u and v are both even, then gcd(u, v) = 2·gcd(u/2, v/2), because 2 is a common divisor.
If u is even and v is odd, then gcd(u, v) = gcd(u/2, v), because 2 is not a common divisor. Similarly, if u is odd and v is even, then gcd(u, v) = gcd(u, v/2).
If u and v are both odd, and u ≥ v, then gcd(u, v) = gcd((u ? v)/2, v). If both are odd and u < v, then gcd(u, v) = gcd((v ? u)/2, u). These are combinations of one step of the simple Euclidean algorithm, which uses subtraction at each step, and an application of step 3 above. The division by 2 results in an integer because the difference of two odd numbers is even.[3]
Repeat steps 2–4 until u = v, or (one more step) until u = 0. In either case, the GCD is 2kv, where k is the number of common factors of 2 found in step 2.
The algorithm requires O(n2)[4] worst-case time, where n is the number of bits in the larger of the two numbers. Although each step reduces at least one of the operands by at least a factor of 2, the subtract and shift operations take linear time for very large integers (although they're still quite fast in practice, requiring about one operation per word of the representation).
Recursive version in C
unsigned int gcd(unsigned int u, unsigned int v)
{
// simple cases (termination)
if (u == v)
return u;
if (u == 0)
return v;
if (v == 0)
return u;
// look for factors of 2
if (~u & 1) // u is even
{
if (v & 1) // v is odd
return gcd(u >> 1, v);
else // both u and v are even
return gcd(u >> 1, v >> 1) << 1;
}
if (~v & 1) // u is odd, v is even
return gcd(u, v >> 1);
// reduce larger argument
if (u > v)
return gcd((u - v) >> 1, v);
return gcd((v - u) >> 1, u);
}
Iterative version in C
It first removes all common factors of 2 using identity 2, then computes the GCD of the remaining numbers using identities 3 and 4, and combines these to form the final answer.
with implementations of binary GCD similar to the above C code, the gain in speed over the Euclidean algorithm is always less in practice than in theory. The reason is that the code uses many data-dependent branches
https://github.com/adnanaziz/EpiCode/blob/master/Java/com/epi/GCD.java
Euclid's GCD Algorithm欧几里得
http://people.cis.ksu.edu/~schmidt/301s12/Exercises/euclid_alg.html
http://en.wikipedia.org/wiki/Euclidean_algorithm
Euclid's insight was to observe that, if x > y, then
GCD(x,y) = GCD(x-y,y)
Proof:
x - y = q1d - q2d = (q1 - q2)d. Therefore d is also a divisor of x-y.
Using similar reasoning, one can show the converse, i.e., that any divisor of x-y and y is also a divisor of x. Hence, the set of common divisors of x and y is the same as the set of common divisors of x-y and y. In particular, the largest values in these two sets are the same, which is to say that GCD(x,y) = GCD(x-y,y).
int gcd(int K, int M) {
int k = K; // In order to state a simple, elegant loop invariant,
int m = M; // we keep the formal arguments constant and use
// local variables to do the calculations.
// loop invariant: GCD(K,M) = GCD(k,m)
while (k != m) {
if (k > m)
{ k = k-m; }
else
{ m = m-k; }
}
// At this point, GCD(K,M) = GCD(k,m) = GCD(k,k) = k
return k;
}
A significant improvement in performance (in some cases) is possible, however, by using the remainder operator (%) rather than subtraction.
int gcd(int K, int M) {
int k = K; // In order to state a simple, elegant loop invariant,
int m = M; // we keep the formal arguments constant and use
// local variables to do the calculations.
// loop invariant: GCD(K,M) = GCD(k,m)
while (k !=0 && m != 0) {
if (k > m)
{ k = k % m; }
else
{ m = m % k; }
}
// At this point, GCD(K,M) = GCD(k,m) = max(k,m)
return Math.max(k,m);
}
Further code-simplification improvements are possible, however, by ensuring that k ≥ m. We can achieve this by replacing, on each iteration, k's value by m's and m's by k % m. This way, no if statement is needed:
int gcd(int K, int M) {
int k = Math.max(K,M);
int m = Math.min(K,M);
// loop invariant: k ≥ m ∧ GCD(K,M) = GCD(k,m)
while (m != 0) {
int r = k % m;
k = m;
m = r;
}
// At this point, GCD(K,M) = GCD(k,m) = GCD(k,0) = k
return k;
}
If you already have gcd for greatest common divisor, then this formula calculates lcm.
One can also find lcm by merging the prime decompositions of both m and n.
Computing the least common multiple of an integer array, using the associative law:
function LCM(A) // A is an integer array (e.g. [-50,25,-45,-18,90,447]) { var n = A.length, a = Math.abs(A[0]); for (var i = 1; i < n; i++) { var b = Math.abs(A[i]), c = a; while (a && b){ a > b ? a %= b : b %= a; } a = Math.abs(c*A[i])/(a+b); } return a; }http://codesam.blogspot.com/2011/04/calculate-least-common-multiple-of-two.html
Not efficient:
int lcm(int num1, int num2)
{
if (num1 % num2 == 0)
return num1;
if (num2 % num1 == 0)
return num2;
int n = (num1 <= num2) ? num2 : num1;
for (; ; n++)
{
if(n % num1 == 0 && n % num2 == 0)
return n;
}
}
http://www.sanfoundry.com/java-program-find-gcd-lcm-two-numbers/static int gcd(int x, int y)
{int r=0, a, b;
a = (x > y) ? x : y; // a is greater number
b = (x < y) ? x : y; // b is smaller number
r = b;
while(a % b != 0)
{r = a % b;
a = b;
b = r;
}return r;
}static int lcm(int x, int y)
{int a;
a = (x > y) ? x : y; // a is greater number
while(true)
{if(a % x == 0 && a % y == 0)
return a;
++a;
}}
long long gcd(long long a, long long b)
{
if (b == 0)return a;
return gcd(b, a%b);
}
long long lcm(long long a, long long b)
{
return a * b / gcd(a, b);
}
gcd(M, N) × lcm(M, N) = M × N.
It follows that to find one is sufficient to find another, for example, gcd(N, M) = N × M / lcm(N, M). gcd alone can be found with Euclid's algorithm; lcm of two or more numbers is produced by the onion algorithm.
http://www.geeksforgeeks.org/steins-algorithm-for-finding-gcd/- If both and b are 0, gcd is zero gcd(0, 0) = 0.
- gcd(a, 0) = a and gcd(0, b) = b because everything divides 0.
- If a and b are both even, gcd(a, b) = 2*gcd(a/2, b/2) because 2 is a common divisor. Multiplication with 2 can be done with bitwise shift operator.
- If a is even and b is odd, gcd(a, b) = gcd(a/2, b). Similarly, if a is odd and b is even, then
gcd(a, b) = gcd(a, b/2). It is because 2 is not a common divisor. - If both a and b are odd, then gcd(a, b) = gcd(|a-b|/2, b). Note that difference of two odd numbers is even
- Repeat steps 3–5 until a = b, or until a = 0. In either case, the GCD is power(2, k) * b, where power(2, k) is 2 raise to the power of k and k is the number of common factors of 2 found in step 2.
Time Complexity: O(N*N) where N is the number of bits in the larger number.
You may also like – Basic and Extended Euclidian Algorithm
References:
- https://en.wikipedia.org/wiki/Binary_GCD_algorithm
- http://andreinc.net/2010/12/12/binary-gcd-steins-algorithm-in-c/
- http://www.cse.unt.edu/~tarau/teaching/PP/NumberTheoretical/GCD/Binary%20GCD%20algorithm.pdf
int gcd(int a, int b){ if (a == b) return a; /* GCD(0,b) == b; GCD(a,0) == a, GCD(0,0) == 0 */ if (a == 0) return b; if (b == 0) return a; // look for factors of 2 if (~a & 1 ) // a is even { if (b & 1) // b is odd return gcd(a >> 1, b); else // both a and b are even return gcd(a >> 1, b >> 1) << 1; } if (~b & 1) // a is odd, b is even return gcd(a, b >> 1); // reduce larger number if (a > b) return gcd((a - b) >> 1, b); return gcd((b - a) >> 1, a);}int gcd(int a, int b){ /* GCD(0, b) == b; GCD(a,0) == a, GCD(0,0) == 0 */ if (a == 0) return b; if (b == 0) return a; /*Finding K, where K is the greatest power of 2 that divides both a and b. */ int k; for (k = 0; ((a | b) & 1) == 0; ++k) { a >>= 1; b >>= 1; } /* Dividing a by 2 until a becomes odd */ while ((a & 1) == 0) a >>= 1; /* From here on, 'a' is always odd. */ do { /* If b is even, remove all factor of 2 in b */ while ((b & 1) == 0) b >>= 1; /* Now a and b are both odd. Swap if necessary so a <= b, then set b = b - a (which is even).*/ if (a > b) swap(a, b); // Swap u and v. b = (b - a); } while (b != 0); /* restore common factors of 2 */ return a << k;}Given an array of numbers, find GCD of the array elements.
The GCD of three or more numbers equals the product of the prime factors common to all the numbers, but it can also be calculated by repeatedly taking the GCDs of pairs of numbers.
gcd(a, b, c) = gcd(a, gcd(b, c))
= gcd(gcd(a, b), c)
= gcd(gcd(a, c), b)
For an array of elements, we do following.
result = arr[0] For i = 1 to n-1 result = GCD(result, arr[i])
int findGCD(int arr[], int n){ int result = arr[0]; for (int i=1; i<n; i++) result = gcd(arr[i], result); return result;}