LeetCode 1254 - Number of Closed Islands

https://leetcode.com/problems/number-of-closed-islands/

Given a 2D grid consists of 0s (land) and 1s (water).  An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

Example 1:

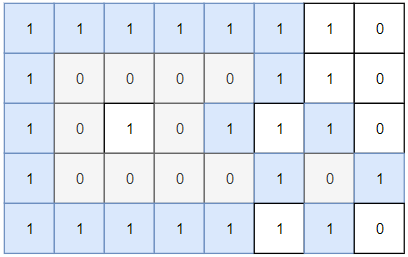
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

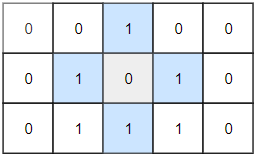
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

Constraints:

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <=1

X. https://leetcode.com/problems/number-of-closed-islands/discuss/425150/JavaC%2B%2B-with-picture-Number-of-Enclaves

This is similar to 1020. Number of Enclaves.

Approach 1: Flood Fill

First, we need to remove all land connected to the edges using flood fill.

Then, we can count and flood-fill the remaining islands.

Complexity Analysis

• Time: O(n), where n is the total number of cells. We flood-fill all land cells once.
• Memory: O(n) for the stack. Flood fill is DFS, and the maximum depth is n.

int fill(int[][] g, int i, int j) {
  if (i < 0 || j < 0 || i >= g.length || j >= g[i].length || g[i][j] != 0)
    return 0;
  return (g[i][j] = 1) + fill(g, i + 1, j) + fill(g, i, j + 1)
    + fill(g, i - 1, j) + fill(g, i, j - 1);
}
public int closedIsland(int[][] g) {
  for (int i = 0; i < g.length; ++i)
    for (int j = 0; j < g[i].length; ++j)
      if (i * j * (i - g.length + 1) * (j - g[i].length + 1) == 0)
        fill(g, i, j);
  int res = 0;
  for (int i = 0; i < g.length; ++i)
    for (int j = 0; j < g[i].length; ++j)
      res += fill(g, i, j) > 0 ? 1 : 0;
  return res;
}

https://zxi.mytechroad.com/blog/searching/leetcode-1254-number-of-closed-islands/
Solution: DFS/Backtracking
For each connected component, if it can reach the boundary then it’s not a closed island.

Time complexity: O(n*m)
Space complexity: O(n*m)

  int closedIsland(vector<vector<int>>& grid) {    

    const int n = grid.size();

    const int m = grid[0].size();    

    function<int(int, int)> dfs = [&](int x, int y) {

      if (x < 0 || y < 0 || x >= m || y >= n) return 0;      

      if (grid[y][x]++) return 1;

      return dfs(x + 1, y) & dfs(x - 1, y) & dfs(x, y + 1) & dfs(x, y - 1);

    };

    

    int ans = 0;

    for (int i = 0; i < n; ++i)

      for (int j = 0; j < m; ++j)

        if (!grid[i][j]) ans += dfs(j, i);      

    return ans;

  }

X. BFS
https://algorithm-notes-allinone.blogspot.com/2019/11/leetcode-1254-number-of-closed-islands.html

1.     int closedIsland(vector<vector<int>>& grid) {
2.         int res = 0;
3.         int m = grid.size(), n = grid[0].size();
4.         vector<vector<int>> visit(m, vector<int>(n, 0));//not needed if we can modify grid' values
5.         for(int i=0; i<m; ++i) {
6.             for(int j=0; j<n; ++j) {
7.                 if(grid[i][j] == 0 && !visit[i][j]) {
8.                     bfs(grid, i, j, visit, res);
9.                 }
10.             }
11.         }
12.         return res;
13.     }
14.  
15. private:
16.     void bfs(vector<vector<int>>& gd, int x, int y, vector<vector<int>>& visit, int &res) {
17.         queue<pair<int, int>> q;
18.         q.push({x, y});
19.         visit[x][y] = 1;
20.         vector<int> dirs = {-1, 0, 1, 0, -1};
21.         bool ed = false;//this is the only difference
22.         while(q.size()) {
23.             auto t = q.front();
24.             q.pop();
25.             for(int i=0; i+1<dirs.size(); ++i) {
26.                 int a = t.first + dirs[i], b = t.second + dirs[i+1];
27.                 if(a<0 || a>= gd.size() || b<0 || b>=gd[0].size()) {
28.                     ed = true;//is edge
29.                     continue;
30.                 }
31.                 if(visit[a][b] || gd[a][b]) continue;
32.                 q.push({a, b});
33.                 visit[a][b] = 1;
34.             }
35.         }
36.         if(!ed) ++res;
37.     }

https://www.cnblogs.com/seyjs/p/11841246.html
https://www.cnblogs.com/onePunchCoder/p/11830972.html

private static final int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

    public int closedIsland(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] visited = new int[m][n];
        boolean flag;
        LinkedList<int[]> queue = new LinkedList<>();
        int result = 0;
        for (int i = 1; i < m - 1; i++) {
            for (int j = 1; j < n - 1; j++) {
                if (grid[i][j] == 0 && visited[i][j] == 0) {
                    flag = true;
                    queue.addLast(new int[]{i, j});
                    int[] island;
                    int I, J;
                    while (!queue.isEmpty()) {
                        island = queue.pollFirst();
                        for (int[] direction : directions) {
                            I = island[0] + direction[0];
                            J = island[1] + direction[1];
                            if (I >= 0 && I < m && J >= 0 && J < n && grid[I][J] == 0 && visited[I][J] == 0) {
                                visited[I][J] = 1;
                                queue.addLast(new int[]{I, J});
                                if (I == 0 || I == m - 1 || J == 0 || J == n - 1) {
                                    flag = false;
                                }
                            }
                        }
                    }
                    if (flag) result++;
                }
            }
        }
        return result;
    }