Area of a polygon with given n ordered vertices - GeeksforGeeks
Given ordered coordinates of a polygon with n vertices. Find area of the polygon. Here ordered mean that the coordinates are given either in clockwise manner or anticlockwise from first vertex to last.
Given ordered coordinates of a polygon with n vertices. Find area of the polygon. Here ordered mean that the coordinates are given either in clockwise manner or anticlockwise from first vertex to last.
Input : X[] = {0, 4, 4, 0}, Y[] = {0, 0, 4, 4};
Output : 16
We can compute area of a polygon using Shoelace formula.
Area= | 1/2 [ (x1y2 + x2y3 + ... + xn-1yn + xny1) - (x2y1 + x3y2 + ... + xnyn-1 + x1yn) ] |
// (X[i], Y[i]) are coordinates of i'th point.double polygonArea(double X[], double Y[], int n){ // Initialze area double area = 0.0; // Calculate value of shoelace formula int j = n - 1; for (int i = 0; i < n; i++) { area += (X[j] + X[i]) * (Y[j] - Y[i]); j = i; // j is previous vertex to i } // Return absolute value return abs(area / 2.0);}
Why is it called Shoelace Formula?
The formula is called so because of the way we evaluate it.
The formula is called so because of the way we evaluate it.
Example:
Let the input vertices be (0, 1), (2, 3), and (4, 7). Evaluation procedure matches with process of tying shoelaces. We write vertices as below 0 1 2 3 4 7 0 1 [written twice] we evaluate positive terms as below 0 \ 1 2 \ 3 4 \ 7 0 1 i.e., 0*3 + 2*7 + 4*1 = 18 we evaluate negative terms as below 0 1 2 / 3 4 / 7 0 / 1 i.e., 0*7 + 4*3 + 2*1 = 14 Area = 1/2 (18 - 14) = 2 See this for a clearer image.
Area(A1A2...An) = ½|∑(xjyj+1 - xj+1yj)| = ½|∑xj(yj+1 - yj-1)|,
where the sum is taken for j = 1, ..., n and the indices are defined cyclically: xn+1 = x1 and x0 = xn and similarly for y's.
For the square with vertices A1(b, 0), A2(a+b, b), A3(a, a+b), A4(0, a), the formula gives
On the other hand, if c is the hypotenuse of the right triangle with vertices (0, 0), (b, 0), and (0, a) then the area of the square formed on the hypotenuse is c², showing that indeed a² + b² = c².
We can always divide a polygon into triangles. The area formula is derived by taking each edge AB, and calculating the (signed) area of triangle ABO with a vertex at the origin O, by taking the cross-product (which gives the area of a parallelogram) and dividing by 2. As one wraps around the polygon, these triangles with positive and negative area will overlap, and the areas between the origin and the polygon will be cancelled out and sum to 0, while only the area inside the reference triangle remains.
Consider the polygon defined by the points (3,4), (5,11), (12,8), (9,5), and (5,6), and illustrated in the following diagram:
The area of this polygon is:
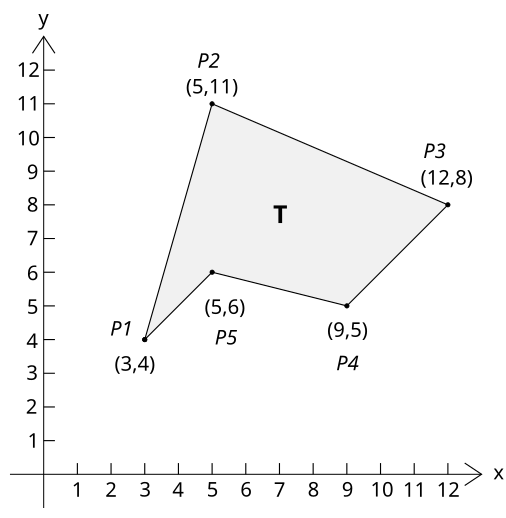
![\begin{align}
\mathbf{A} & = {1 \over 2}|3 \times 11 + 5 \times 8 + 12 \times 5 + 9 \times 6 + 5 \times 4 \\
& {} \qquad {} - 4 \times 5 - 11 \times 12 - 8 \times 9 - 5 \times 5 - 6 \times 3| \\[10pt]
& = {60 \over 2} = 30
\end{align}](https://upload.wikimedia.org/math/9/5/0/950a88a5f467bf92c6eccb9f4c9096c7.png)